Keywords: Semiparametric Bayesian methods ● Growth curve modeling ● Robust analysis ● Dirichlet process mixture
Longitudinal studies help us understand changes. Unlike one-off cross-sectional studies that give information about subjects at one point, like a snapshot photo, longitudinal studies follow subjects across time, more like a photo album. They tell a story of subjects not only at a moment in time, but also over time, showing how subjects have changed and what factors have caused between-subjects variations in change. Growth curve models are widely used in longitudinal research (e.g., McArdle & Nesselroade, 2014) as many longitudinal models in social and behavioral sciences, such as multilevel models and linear hierarchical models, can be written as a form of growth curve models. In practice, traditional growth curve model estimation is based on the assumption that both random effects and within-subject measurement errors are normally distributed. However, data in social and behavioral sciences are rarely normal and may be contaminated by outliers (Cain et al., 2017; Micceri, 1989). Because ignoring the nonnormality of data may lead to imprecise or even inaccurate parameter estimates and misleading statistical inferences (e.g., Maronna et al., 2006; Yuan & Bentler, 2001), and routine methods, such as deleting the outliers, may lead to problems such as resulting inferences failing to reflect uncertainty and reduced efficiency (e.g., Lange et al., 1989; Yuan & Bentler, 2002), researchers have developed robust methods to obtain reliable parameter estimation and statistical inference.
The basic ideas of robust methods often include two types. The first type is to assign a weight to each subject in a dataset according to its distance from the center of the majority of the data aiming to downweight potential outlying observations (e.g., Pendergast & Broffitt, 1985; Silvapulle, 1992; Singer & Sen, 1986; Yuan & Bentler, 1998; Zhong & Yuan, 2010). The second type is to use certain nonnormal distributions that are mathematically tractable, instead of normal distributions, to model data distributions. Both types of robust methods have been directly applied to growth curve modeling. For example, on the one hand, Pendergast & Broffitt (1985) and Singer & Sen (1986) proposed robust estimators based on M-methods for growth curve models with elliptically symmetric errors, and Silvapulle (1992) further extended the M-method to allow asymmetric errors for growth curve analysis. Yuan & Zhang (2012) developed a two-stage robust procedure for structural equation modeling with nonnormal missing data and applied the procedure to growth curve modeling. On the other hand, latent variables and/or measurement errors were assumed to follow a $t$ or skew-$t$ distribution (Tong & Zhang, 2012; Zhang, 2016) or a mixture of certain distributions (Lu & Zhang, 2014; Muthén & Shedden, 1999). While being useful, these methods still have limitations under certain conditions. For example, the downweighting method did not perform well when latent variables contain extreme scores (e.g., see simulation results in Zhong & Yuan, 2011). Using a $t$ distribution or a mixture of normal distributions still imposed restrictions on the shape of the data distribution.
Semiparametric Bayesian methods, also referred to as nonparametric Bayesian methods, can solve these issues as they are more flexible to relax the normality assumptions. Semiparametric Bayesian modeling relies on a building block, Dirichlet process (DP), which is a distribution over probability measures that can be used to estimate unknown distributions. Therefore, the nonnormality issue can be addressed by directly estimating the unknown random distributions of latent variables or measurement errors (i.e., obtaining the posteriors of the distributions). The advantages of using Semiparametric Bayesian methods have been discussed in the literature (e.g., Fahrmeir & Raach, 2007; Ghosal et al., 1999; Hjort, 2003; Hjort et al., 2010; MacEachern, 1999; Müller & Mitra, 2004). First, they do not constrain models to a specific parametric form that may limit the scope and type of statistical inferences in many situations. Second, they can provide full probability models for the data-generating process and lead to analytically tractable posterior distributions.
Because of their flexibility and adaptivity, semiparametric Bayesian methods have been applied to various models. Bush & MacEachern (1996), Kleinman & Ibrahim (1998), and Brown & Ibrahim (2003) used DP mixtures to handle nonnormal random effects. Burr & Doss (2005) used a conditional DP to handle heterogeneous effect sizes in meta-analysis. Ansari & Iyengar (2006) included Dirichlet components to build a semiparametric recurrent choice model. Si & Reiter (2013) used DP mixtures of multinomial distributions for categorical data with missing values. Semiparametric Bayesian methods have also been applied to structural equation modeling to relax the normality assumption of the latent variables (e.g., Lee et al., 2008; Yang & Dunson, 2010). Tong & Zhang (2019) directly used a DP mixture to model nonnormal data in growth curve modeling. Although it has been shown in Tong & Zhang (2019) that semiparametric Bayesian methods outperformed traditional growth curve modeling as well as Student’s $t$-distribution-based robust method when data were not normal, nonnormal data were generated with measurement errors nonnormally distributed and only measurement errors were modeled using semiparametric Bayesian methods. In practice, it is possible that random effects also violate the normality assumption. To account for this issue, we need to also model random effects semiparametrically.
Therefore, in this study, three different types of robust distributional growth curve models are proposed from a semiparametric Bayesian perspective. The features of these three types of models as well as traditional growth curve model are also discussed. In the next two sections, after introducing the idea of semiparametric Bayesian modeling, we introduce three types of semiparametric Bayesian growth curve models. Then, we compare the three types of models and the traditional model in modeling different types of data through simulation studies. Recommendations are provided at the end of the article.
A typical motivation of using semiparametric Bayesian methods is that one is unwilling to make unverified assumptions for latent variables or measurement error distributions as in the parametric modeling. Under a semiparametric perspective, we model the distribution of a random vector $\boldsymbol {\xi }$ using a random distribution function $G$ with a prior $\mathcal {G}$. Namely, the traditional parametric assumption of the random vector $\boldsymbol {\xi }$ (i.e., $\boldsymbol {\xi }\sim N(\boldsymbol {\mu _{\xi }},\boldsymbol {\Phi _{\xi }})$) is replaced by
The DP is characterized by the two parameters, $\alpha $ and $G_{0}$. $G_{0}$ is a base distribution, which represents the central or “mean” distribution in the distribution space, while the precision parameter $\alpha $ governs how close realizations of $G$ are to $G_{0}$. For example, Figure 1 displays generated random distributions from the Dirichlet process given $G_{0}$ and different values of $\alpha $. The red lines in the four plots represent the cumulative density curve for the base distribution $G_{0}$, which is a standard normal distribution in this case. Black lines in each figure represent $G$s generated from the Dirichlet process in five replications given $G_{0}$ and $\alpha $. Clearly, as $\alpha $ increases, generated $G$s are closer to $G_{0}$.
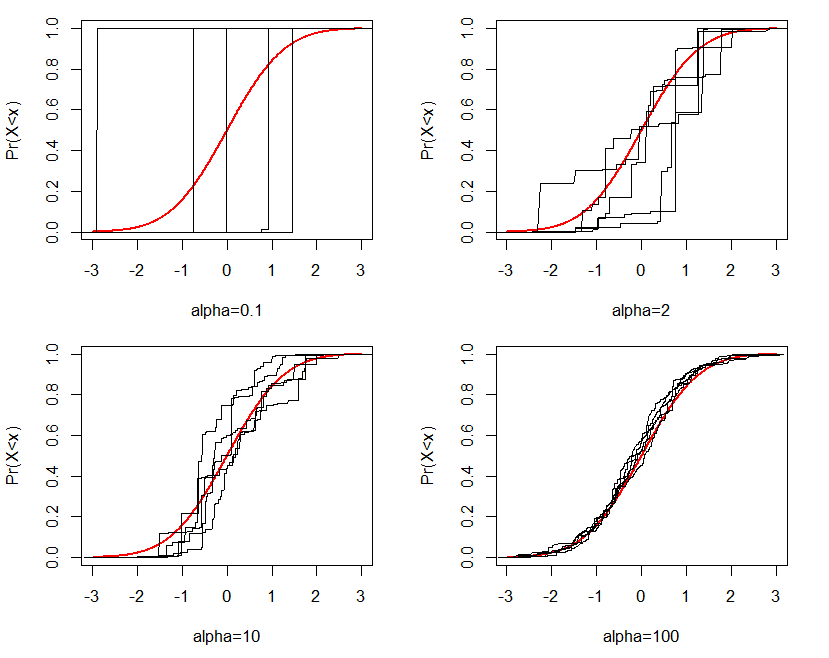
Ferguson (1973) introduced the DP as a random probability measure that has two desirable properties: (1) its support is sufficiently large, and (2) the posterior distribution is analytically manageable. He explained that the Dirichlet process is a conjugate prior and the posterior of $G$ is $DP(\tilde {\alpha },\tilde {G_{0}})$. The two parameters $\tilde {\alpha }=\alpha +N$ and \[ \tilde {G_{0}}=\dfrac {\alpha }{\alpha +N}G_{0}+\dfrac {N}{\alpha +N}G_{N}, \] where $G_{N}$ is the empirical distribution function of the data. Thus, the posterior point estimate of $G$, $E(G|data)=\tilde {G_{0}}$, is a weighted average of two distributions: $G_{0}$ and $G_{N}$. If $\alpha =0$, the posterior point estimate is $G_{N}$, which is nonparametric. When $\alpha $ approaches infinity, the posterior point estimate approaches to $G_{0}$, which is parametric. In practice, $\alpha \sim Gamma(a_{1},a_{2})$, which is neither 0 nor infinity. Thus, we consider the posterior point estimate of $G$ as semiparametric.
Sethuraman (1994) developed a constructive way of forming $G$, known as “stick-breaking”, and showed that draws from stick-breaking are indeed DP distributed under very general conditions. Let $q_{1},q_{2},\ldots ,q_{k},\ldots \sim Beta(1,\alpha )$. Define \[ p_{k}=q_{k}\prod _{j=1}^{k-1}(1-q_{j}). \] Then, \[ G=\sum _{k=1}^{\infty }p_{k}\delta _{\boldsymbol {\xi }_{k}^{*}}, \] where $\delta _{\boldsymbol {\xi }_{k}^{*}}$ is the Dirac probability measure and $\boldsymbol {\xi }_{k}^{*}\sim G_{0}$. It is important to note that $\sum _{k=1}^{\infty }p_{k}=1$ as it guarantees $G$ to be a distribution.
The process of the stick-breaking construction is given below.
1. Draw $\boldsymbol {\xi }_{1}^{*}$ from $G_{0}$;
2. Draw $q_{1}$ from $Beta(1,\alpha )$, then $p_{1}=q_{1}$;
3. Draw $\boldsymbol {\xi }_{2}^{*}$ from $G_{0}$;
4. Draw $q_{2}$ from $Beta(1,\alpha )$, then $p_{2}=q_{2}(1-q_{1})$;
...
Therefore, the distribution $G(\cdot )$ is a discrete distribution as \[ G(\cdot )=\begin {cases} \boldsymbol {\xi }_{1}^{*}, & p=p_{1}\\ \boldsymbol {\xi }_{2}^{*}, & p=p_{2}\\ \vdots & \vdots \\ \boldsymbol {\xi }_{k}^{*}, & p=p_{k}\\ \vdots & \vdots \end {cases}. \] To define a continuous distribution, the Dirichlet process can be used as the basis of a mixture model, for example, a mixture of $N(\mu _{k},\sigma _{k}^{2})$ with mixing proportions defined by $p_{k}$. Theoretically, there are an infinite number of mixture components as $k=1,\ldots ,\infty $, given an arbitrarily flexible choice of distributional shapes. Multimodal or heavy-tailed distributions can be naturally modeled in this way. In practice, a finite number of mixture components would be good enough, and this number is taken into account by the Dirichlet process. Smaller values of DP precision parameter $\alpha $ result in a smaller number of mixture components.
Consider a longitudinal dataset with $N$ subjects and $T$ measurement occasions. Let $\mathbf {y}_{i}=(y_{i1},\ldots ,y_{iT})'$ be a $T\times 1$ random vector with $y_{ij}$ being an observation from subject $i$ at time $j$ ($i=1,\ldots ,N;j=1,\ldots ,T$). A typical growth curve model can be written as
where $\bf \Lambda $ is a $T\times q$ factor loading matrix that determines the growth curves, ${\bf b}_{i}$ is a $q\times 1$ vector of random effects, and ${\bf e}_{i}$ is a vector of measurement errors. The vector of random effects ${\bf b}_{i}$ varies around its mean $\boldsymbol {\beta }$. The residual vector ${\bf u}_{i}$ represents the deviation of ${\bf b}_{i}$ from $\boldsymbol {\beta }$. When \[ \boldsymbol {\Lambda }=\left (\begin {array}{cc} 1 & 0\\ 1 & 1\\ \vdots & \vdots \\ 1 & T-1 \end {array}\right ),\mathbf {b}_{i}=\left (\begin {array}{c} L_{i}\\ S_{i} \end {array}\right ),\ and\ \boldsymbol {\beta }=\left (\begin {array}{c} \beta _{L}\\ \beta _{S} \end {array}\right ), \] the model is reduced to a linear growth curve model with random intercept $L_{i}$ and random slope $S_{i}$. The mean intercept and slope are denoted as $\beta _{L}$ and $\beta _{S}$, respectively.
Traditionally, ${\bf e}_{i}$ and ${\bf u}_{i}$ are assumed to follow multivariate normal distributions with mean vectors of zero and covariance matrices $\boldsymbol {\Phi }$ and $\boldsymbol {\Psi }$, respectively, so ${\bf e}_{i}\sim MN_{T}(\mathbf {0},\boldsymbol {\Phi })$ and ${\bf u}_{i}\sim MN_{q}(\mathbf {0},\boldsymbol {\Psi })$, where $MN$ denotes a multivariate normal distribution and its subscript indicates its dimension. Although traditional growth curve models are widely used, they can be deficient because practical data often violate the normality assumption. Tong & Zhang (2019) proposed to model ${\bf e}_{i}$ using semiparametric Bayesian methods to account for the nonnormality of data. However, since the nonnormality of a growth curve model may come from two resources – the measurement errors ${\bf e}_{i}$ and the random components ${\bf u}_{i}$ (Pinheiro et al., 2001), we model either one or both of them semiparametrically and propose three types of robust distributional growth curve models. The first type of robust semiparametric Bayesian growth curve models is the same as what Tong & Zhang (2019) proposed: we let ${\bf e}_{i}\sim G_{e},\ G_{e}\sim DP$ and keep ${\bf u}_{i}\sim MN_{q}(\mathbf {0},\boldsymbol {\Psi })$. The second type of robust growth curve models can be derived by keeping ${\bf e}_{i}\sim MN_{T}(0,\boldsymbol {\Phi })$ and letting ${\bf u}_{i}\sim G_{u},G_{u}\sim DP$. The third type of robust growth curve model can be obtained by letting ${\bf e}_{i}\sim G_{e},\ G_{e}\sim DP$ and ${\bf u}_{i}\sim G_{u},G_{u}\sim DP$. We denote the three types of robust growth curve models as the Semi-N distributional model, the N-Semi distributional model, and the Semi-Semi distributional model, respectively. Similarly, we also denote the traditional growth curve model as the N-N distributional model.
In the Semi-N distributional model, we assume that ${\bf e}_{i}\sim G_{e}$ where $G_{e}$ is an unknown random distribution that is determined by the data. Because the distribution of ${\bf e}_{i}$ is continuous, a DP mixture (DPM) can be used to model the measurement errors such that \[ G_{e}=\begin {cases} D(\boldsymbol {\mu }_{e}^{(1)},\boldsymbol {\Phi }^{(1)}), & with\ p=p_{1}\\ D(\boldsymbol {\mu }_{e}^{(2)},\boldsymbol {\Phi }^{(2)}), & with\ p=p_{2}\\ \vdots & \vdots \\ D(\boldsymbol {\mu }_{e}^{(k)},\boldsymbol {\Phi }^{(k)}), & with\ p=p_{k}\\ \vdots & \vdots \end {cases}, \] where $D$ represents a predetermined multivariate distribution (e.g., multivariate normal, $t$, multinomial, etc.), and $\boldsymbol {\mu }_{e}^{(k)}\ \mbox {and}\ \boldsymbol {\Phi }^{(k)},k=1,\ldots ,\infty $ are means and covariances of the multivariate distribution in the $k$th component with probability $p_{k}$. Tong & Zhang (2019) proposed that
That is, the unknown distribution $G_{e}$ is approximated by a mixture of multivariate normal distributions where the mixing measure has a Dirichlet process prior, $G_{e}\sim DPM$. The DP prior $DP(\alpha ,G_{0})$ can be obtained using the truncated stick-breaking construction (e.g., Lunn et al., 2013; Sethuraman, 1994). Specifically, $DP(\cdot )=\sum _{j=1}^{C}p_{j}\delta _{z_{j}}(\cdot ),1\leq C<\infty $, where $C$ ($1\leq C\leq N,$often set at a large number) is a possible maximum number of mixture components, $\delta _{z_{j}}(\cdot )$ denotes a point mass at $z_{j}$ and $z_{j}\sim G_{0}$ independently. The random weights $p_{j}$ can be generated through the following procedure. With $q_{1},q_{2},\ldots ,q_{C}\sim Beta(1,\alpha )$, define \[ p_{j}^{'}=q_{j}\prod _{k=1}^{j-1}(1-q_{k}),j=1,\ldots ,C. \] Then, $p_{j}$ is obtained by \[ p_{j}=\dfrac {p_{j}^{'}}{\sum _{k=1}^{C}p_{k}^{'}}, \] to satisfy that $\sum _{j=1}^{C}p_{j}=1$.
Thus, the distribution of ${\bf e}_{i}$ through the truncated stick-breaking construction is \[ G_{e}=\begin {cases} MN(\boldsymbol {\mu }_{e}^{(1)},\boldsymbol {\Phi }^{(1)}), & with\ p=p_{1}\\ MN(\boldsymbol {\mu }_{e}^{(2)},\boldsymbol {\Phi }^{(2)}), & with\ p=p_{2}\\ \vdots & \vdots \\ MN(\boldsymbol {\mu }_{e}^{(C)},\boldsymbol {\Phi }^{(C)}), & with\ p=p_{C} \end {cases}. \] Given that the mean of $\mathbf {e}_{i}$ is $\mathbf {0}$, we constrain $\sum _{j=1}^{C}p_{j}\boldsymbol {\mu }_{e}^{(j)}=\mathbf {0}$. For simplicity, we follow Tong & Zhang (2019) and constrain $\boldsymbol {\mu }_{e}^{(j)}$ to be 0. We use inverse Wishart priors $p(\boldsymbol {\Phi }^{(j)})=IW(n_{0},W_{0})$ for the covariance matrices of the mixture components, $\boldsymbol {\Phi }^{(j)}$, $j=1,\ldots ,C$. Following Lunn et al. (2013, page 294), we fix the shape parameter $n_{0}$ at a specific number and assign an inverse Wishart prior to the scale matrix $W_{0}$. With such a specification, the measurement error for subject $i$, $\mathbf {e}_{i}$, has a $p_{j}$ probability of coming from the mixing component $MN(\mathbf {0},\boldsymbol {\Phi }^{(j)})$. If $\mathbf {e}_{i},i=1,\ldots ,N$ are from $K_{e}$ different distributions among $MN(\mathbf {0},\boldsymbol {\Phi }^{(j)}),j=1,\ldots ,C$, $K_{e}$ is called the number of clusters for $\mathbf {e}_{i}$. Clearly, $K_{e}\leq C$, and within each cluster, $\mathbf {e}_{i}$s come from the same distribution.
Bayesian methods are applied to estimate the model. The key idea of Bayesian methods is to compute the posterior distributions for model parameters by combining the likelihood function and the priors. Recall that in traditional N-N distributional growth curve model, $\boldsymbol {\beta },\boldsymbol {\Phi },$ and $\boldsymbol {\Psi }$ are the model parameters. Here in the Semi-N model, $\boldsymbol {\beta }$ and $\boldsymbol {\Psi }$ are still model parameters and can be estimated in the same way. However, instead of estimating $\boldsymbol {\Phi }$ as in the N-N model, we obtain $\mathbf {e}_{i}$ and $K_{e}$. The estimate of $K_{e}$ indicates the heterogeneity of between-subject measurement errors $\mathbf {e}_{i}$. With a larger value of $K_{e}$, we are more confident to conclude that different subjects’ measurement errors are distributed differently. To obtain an estimate of $\boldsymbol {\Phi }$ (the covariance matrix of $\mathbf {e}_{i}$), we let $\mathbf {e}_{i(s)},i=1,\ldots ,N$ be the observations of $\mathbf {e}_{i}$ simulated from the posterior distribution in the $s$th Gibbs sampler iteration, and let $\boldsymbol {\Phi }_{(s)}$ be the corresponding sample covariance matrix. An estimate of $\boldsymbol {\Phi }$ can be taken as the mean of $\boldsymbol {\Phi }_{(s)}$, averaging over all the Gibbs sampler iterations after the burn-in period.
In the N-Semi model, $\mathbf {u}_{i}$ follow an unknown distribution $G_{u}$ with a Dirichlet process prior. We can obtain the mixing proportion $p_{k}$ and construct the distribution $G_{u}$ in a similar way as in the Semi-N model. \[ G_{u}=\begin {cases} MN(\boldsymbol {\mu }_{u}^{(1)},\boldsymbol {\Psi }^{(1)}), & p=p_{1}\\ MN(\boldsymbol {\mu }_{u}^{(2)},\boldsymbol {\Psi }^{(2)}), & p=p_{2}\\ \vdots & \vdots \\ MN(\boldsymbol {\mu }_{u}^{(C)},\boldsymbol {\Psi }^{(C)}), & p=p_{C} \end {cases}, \] where $\boldsymbol {\mu }_{u}^{(k)}\ \mbox {and}\ \boldsymbol {\Psi }^{(k)},k=1,\ldots ,C$ are parameters of the multivariate normal distribution in the $k$th component. Since $\mathbf {u}_{i}$ represents the random component of the random effects $\mathbf {b}_{i}$, it is also reasonable to set $\boldsymbol {\mu }_{u}^{(k)}=\mathbf {0}$. For the covariance matrices of the mixture components, $\boldsymbol {\Psi }^{(k)}$, inverse Wishart priors are used \[ p(\boldsymbol {\Psi }^{(k)})=IW(m_{0},V_{0}), \] where $m_{0}$ and $V_{0}$ are hyperparameters.
Therefore, $\mathbf {u}_{i}$ comes from $MN(\mathbf {0},\boldsymbol {\Psi }^{(k)})$ with the probability $p_{k}$. The number of clusters for $\mathbf {u}_{i}$ is denoted by $K_{u}$. Within each cluster, $\mathbf {u}_{i}$s come from the same distribution.
In contrast to the N-N and Semi-N distributional growth curve models, in the N-Semi model, we obtain $\mathbf {u}_{i}$ and $K_{u}$ in the Markov chain Monte Carlo (MCMC) procedure instead of estimating $\boldsymbol {\Psi }$, while the fixed effects $\boldsymbol {\beta }$ and the covariance matrix of measurement errors $\boldsymbol {\Phi }$ are still model parameters and estimated in the same way. The estimate of $K_{u}$ indicates the heterogeneity of random effects for different subjects. If $K_{u}$ is large, we are more confident to conclude that different subjects have different growth trajectories. To obtain an estimate of $\boldsymbol {\Psi }$ (the covariance matrix of $\mathbf {u}_{i}$), we let $\mathbf {u}_{i(s)},i=1,\ldots ,N$ be the observations of $\mathbf {u}_{i}$ simulated from the posterior distribution in the $s$th Gibbs sampler iteration, and let $\boldsymbol {\Psi }_{(s)}$ be the corresponding sample covariance matrix. An estimate of $\boldsymbol {\Psi }$ is the mean of $\boldsymbol {\Psi }_{(s)}$, averaging over all the Gibbs sampler iterations after the burn-in period. For the linear growth curve model, the estimate $\hat {\boldsymbol {\Psi }}$ is a $2\times 2$ matrix $((\hat {\sigma }_{L}^{2},\hat {\sigma }_{LS})',(\hat {\sigma }_{LS},\hat {\sigma }_{S}^{2})')$. The significance of $\hat {\sigma }_{L}^{2}$ and $\hat {\sigma }_{S}^{2}$ imply the existence of between-subject differences in the initial level and the rate of change, respectively. A significant $\hat {\sigma }_{LS}$ means that the initial level and the rate of change are significantly correlated.
In the Semi-Semi model, both $\mathbf {e}_{i}$ and $\mathbf {u}_{i}$ follow unknown distributions $G_{e}$ and $G_{u}$, separately. The two distributions can be constructed in the same way as in the Semi-N and N-Semi distributional models. Consequently, we cannot obtain both the estimates of $\boldsymbol {\Phi }$ and $\boldsymbol {\Psi }$ directly, but they can be calculated following the same procedure as discussed in previous sections, and be interpreted likewise. Besides $\boldsymbol {\Phi }$ and $\boldsymbol {\Psi }$, other model parameters include $\boldsymbol {\beta },\ K_{e}$, and $K_{u}$, which can be estimated explicitly in the MCMC procedure. The fixed effect $\boldsymbol {\beta }$ represents the average initial level and rate of change for all subjects. The number of clusters for $\mathbf {e}_{i}$ and the number of clusters for $\mathbf {u}_{i}$ are $K_{e}$ and $K_{u}$, indicating the heteroscedasticities of $\mathbf {e}_{i}$ and $\mathbf {u}_{i}$, respectively.
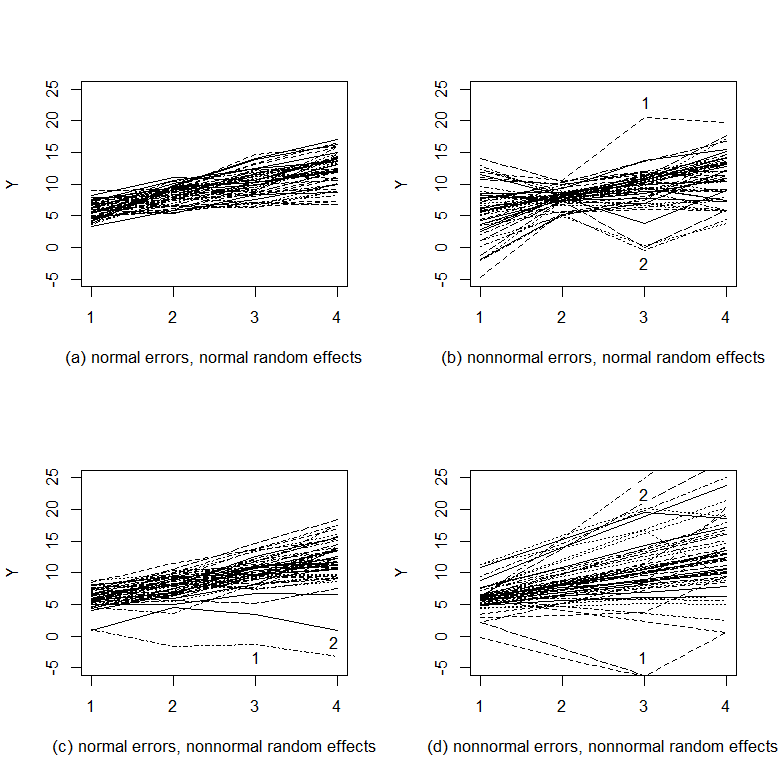
To illustrate the differences among the N-N, Semi-N, N-Semi, and Semi-Semi distributional models, we generate and plot data from the four types of models (Figure 2). For each type of model, data on 50 subjects are generated at four occasions assuming a linear growth trend. Figure 2(a) displays the trajectories of the data generated from the N-N distributional model. No outlier can be observed. The overall trajectory looks clean and smooth. Figure 2(b) plots the data generated from the Semi-N distributional model with nonnormal measurement errors and normal random effects. Noticeably, some observations stand out of the overall trajectory such as those labeled by 1 and 2. A close look at the two observations reveals that the reason why they deviate from the overall trajectory is that they are off their own growth trajectories. Figure 2(c) portrays data from the N-Semi distributional model with normal measurement errors but nonnormal random effects. Some observations also deviate from the overall growth trajectory. However, it seems that those observations are still on their own growth trajectories. The reason why they stand out is that the rate of growth for the specific case is very different from the majority of cases. Figure 2(d) draws the trajectories for the data from the Semi-Semi distributional model with both nonnormal errors and random effects. Clearly, the outlying observations are due to two sources - the trajectory of a case deviates from the overall trajectory and the observation for this specific case is off its own trajectory. For example, observation 1 stands out because it is off the trajectory of the case and the case itself has a lower initial level and a lower rate of change. In summary, Figure 2 suggests that the four types of distributional growth curve models can imply very different patterns in growth trajectories. For instance, if a subject’s growth trajectory is within the normal range of the overall trajectory and an observation at certain times stands out, the data are more likely to come from the Semi-N distributional model. If, within a subject, observations follow a smooth pattern but the trajectory itself differs from the overall trajectory, the data are more likely to come from the N-Semi distributional model. Therefore, given an empirical data set, it is very important to specify the correct type of growth curve models. In order to concretely demonstrate the possible adverse effects of misspecification for finite samples, we conduct a simulation study in the next section.
In this simulation study, we aim to evaluate the performance of the three robust distributional models as well as the traditional N-N model. Moreover, the effects of the misspecification of the three types of robust distributional growth curve models will be studied to compare the intrinsic characteristics of them. We first generate data from the N-N, Semi-N, N-Semi, and Semi-Semi distributional models and name the data as N-N data, Semi-N data, N-Semi data, and Semi-Semi data, respectively. Then, for each type of data, we fit all four types of models and compare their parameter estimates.
We focus on a linear growth curve model as discussed in the previous section
In the model (see Figure 3), the fixed effects are given by $\boldsymbol {\beta }=\left (\beta _{L},\beta _{S}\right )^{'}=\left (6.2,0.3\right )^{'}$.
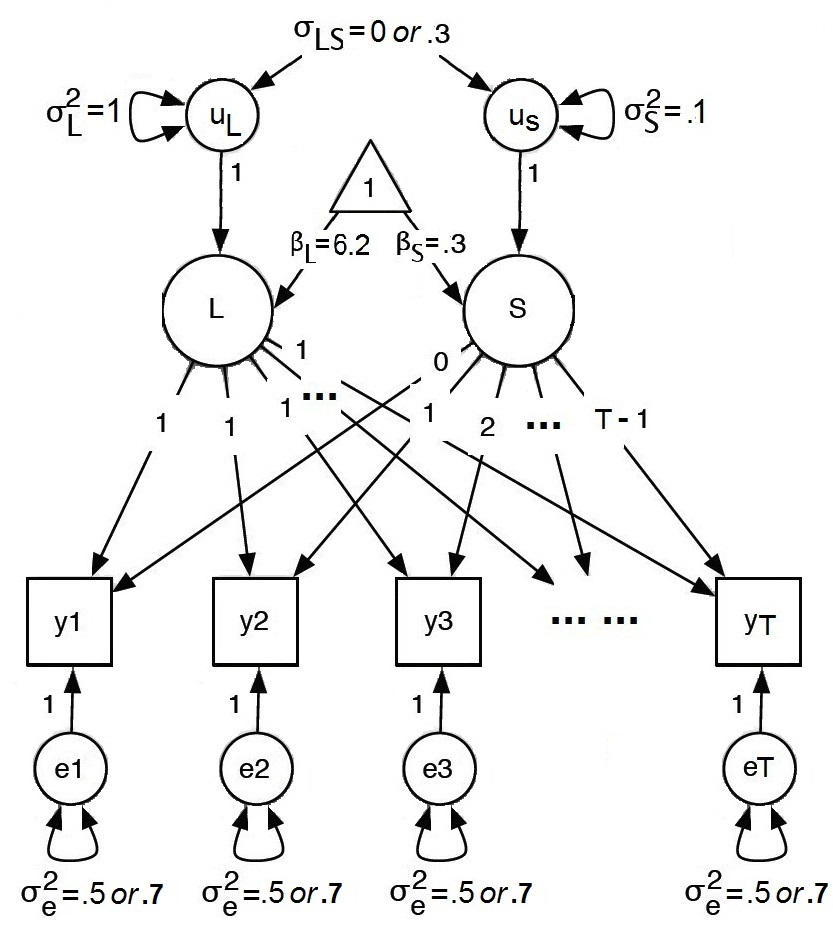
In this study, seven possible influential factors are studied (see Table 1): type of model, type of data, potential number of clusters ($C$), sample size ($N$), number of measurement occasions ($T$), the covariance between the latent intercept and slope ($\sigma _{LS}$), and variance of measurement errors ($\sigma _{e}^{2}$).
First, four types of distributional growth curve models are considered, including the N-N, Semi-N, N-Semi, and Semi-Semi distributional models. Second, based on the four types of models, we generate four types of data, called N-N data, Semi-N data, N-Semi data, and Semi-Semi data correspondingly. We use each one of the four models to fit all four types of data under different conditions of the other five influential factors as described below.
(1) Three different sample sizes are considered: $N=$50, 200, and 500. (2) The number of measurement occasions $T$ is either 3 or 5. (3) For the semiparametric models, we assume that data are potentially from 5 or 20 different clusters. (4) For the growth curve model parameters, the covariance between the latent intercept and the slope $\sigma _{LS}$ is either 0 or 0.3, reflecting uncorrelated and correlated coefficients, respectively. When we generate ${\bf u}_{i}$ from the semiparametric perspective, we simply generate $\boldsymbol {\Psi }^{(k)}\sim IW(m_{0},(m_{0}-2-1)\boldsymbol {\Psi })$ where $\boldsymbol {\Psi =}((\sigma _{L}^{2},\sigma _{LS})',(\sigma _{LS},\sigma _{S}^{2})')$ and the hyperparameter $m_{0}=4$ so that the mean of $\boldsymbol {\Psi }^{(k)}$ is $\boldsymbol {\Psi }$ and thus the “mean” of $G_{u}$ is a distribution with its covariance matrix being $\boldsymbol {\Psi }$. (5) In practice, it is typical to assume the independence of measurement errors and the homogeneity of error variances across time, so the within-subject measurement error structure is usually simplified to $\boldsymbol {\Phi }=\sigma _{e}^{2}\mathbf {I}$. The variance of measurement errors $\sigma _{e}^{2}$ is manipulated to be 0.5 or 0.7 to investigate the influence of measurement errors. When we generate ${\bf e}_{i}=(e_{i1},\ldots ,e_{iT})'$ semiparametrically, we can set $\boldsymbol {\Phi }^{(k)}\sim IW(n_{0},(n_{0}-T-1)\sigma _{e}^{2}\mathbf {I})$. However, in practice, it is easier to generate $e_{i1},\ldots ,e_{iT}$ separately from a univariate distribution $N(0,\sigma _{e}^{2(k)})$. We generate $\sigma _{e}^{2(k)}$ from $\sigma _{e}^{2(k)}\sim IG(c_{0},d_{0})$, where $c_{0}=2$ and $d_{0}=\sigma _{e}^{2}$ so that the mean of $\sigma _{e}^{2(k)}$ is $d_{0}/(c_{0}-1)=\sigma _{e}^{2}$.
| Factor | # of factor levels | Levels |
| Type of model | 4 | N-N model, Semi-N model, N-Semi model, Semi-Semi model |
| Type of data | 4 | N-N data, Semi-N data, N-Semi data, Semi-Semi data |
| # of clusters | 3 | 5, 20 |
| Sample size | 2 | 50, 200, 500 |
| # of measurement occasion | 2 | 3, 5 |
| Var(measurement errors) | 2 | 0.5, 0.7 |
| Cov(intercept, slope) | 2 | 0, 0.3 |
Overall, 768 conditions of simulations are considered. For each condition, a total of 200 data sets are generated and analyzed in OpenBUGS (Lunn et al., 2013).
1. Set $C$ equal to the number of clusters;
2. Generate $p1_{k}$, $k=1,...,C$ ;
3. Generate $\sigma _{e}^{2(k)}\sim IG(c_{0},d_{0})$;
4. Generate $p2_{k}$, $k=1,...,C$;
5. Generate $\boldsymbol {\Psi }^{(k)}\sim IW(m_{0},(m_{0}-2-1)\boldsymbol {\Psi })$;
6. For $i$ in $1:N$, do
(a) Randomly select a cluster based on $p1_{k}$;
(b) If the $k_{1}$th cluster is selected in (a), generate $e_{i1},\ldots ,e_{iT}\sim N(0,\sigma _{e}^{2(k_{1})})$ and let ${\bf e}_{i}=(e_{i1},\ldots ,e_{iT})'$;
(c) Randomly select a cluster based on $p2_{k}$;
(d) If the $k_{2}$th cluster is selected in (c), generate $\mathbf {u}_{i}\sim MN(0,\boldsymbol {\Psi }^{(k_{2})})$;
(e) Generate $\mathbf {y}_{i}=\boldsymbol {\Lambda }\boldsymbol {\beta }+\boldsymbol {\Lambda }\mathbf {u}_{i}+\mathbf {e}_{i}$.
We obtain the parameter estimate, bias, relative bias, empirical standard error, mean square error (MSE), and coverage probability (CP) of the 95% highest posterior density (HPD) credible intervals 1 for each parameter. Let $\theta $ denote a parameter and also its population value, and let $\hat {\theta }_{r}$, $r=1,\ldots ,200$ denote its estimates from the $r$th simulation replication. Furthermore, let $\hat {l}_{r}$ and $\hat {u}_{r}$ denote the lower and upper limits of the 95% HPD credible interval for $\theta $, respectively. Then, the parameter estimate of $\theta $, $\hat {\theta }$, is calculated as the average of parameter estimates of 200 simulation replications \[ \hat {\theta }=\dfrac {1}{200}\sum _{r=1}^{200}\hat {\theta }_{r}. \] The bias of $\hat {\theta }$ is $bias(\hat {\theta })=\hat {\theta }-\theta $. The relative bias of $\hat {\theta }$ is \[ RB(\hat {\theta })=\begin {cases} 100\times \left (\dfrac {\hat {\theta }}{\theta }-1\right ) & \theta \neq 0,\\ 100\times \hat {\theta } & \theta =0. \end {cases} \] Note that the relative bias is rescaled by multiplying 100. Smaller relative bias indicates that the point estimate is less biased and thus more accurate. The empirical standard error is defined by \[ SE(\hat {\theta })=\dfrac {1}{199}\sum _{r=1}^{200}\left (\hat {\theta }_{r}-\hat {\theta }\right )^{2}. \] The mean square error is calculated by $MSE(\hat {\theta })=bias(\hat {\theta })^{2}+SE(\hat {\theta })^{2}$. The CP is calculated as \[ CP(\hat {\theta })=\dfrac {\#(\hat {l}_{r}<\theta <\hat {u}_{r})}{200}, \] where $\#(\hat {l}_{r}<\theta <\hat {u}_{r})$ is the total number of replications with credible intervals covering the true parameter value $\theta $. Good 95% HPD credible intervals should give coverage probabilities close to 0.95.
In this part, we evaluate the performance of the semiparametric models through comparing them with the traditional N-N model in parameter estimation.
First, when data are normally distributed, the four models perform equally well, especially for large sample sizes. For example, Table 2 contains the absolute bias and the standard errors for the six important model parameters ($\beta _{L}$, $\beta _{S}$, $\sigma _{L}^{2}$, $\sigma _{S}^{2}$, $\sigma _{LS}$, and $\sigma _{e}^{2}$) of the four distributional models, when data are generated from the N-N model with $N=500$, $T=5$, $C=20$, $\sigma _{LS}=0.3$, and $\sigma _{e}^{2}=0.5$. Apparently, there is no notable difference in the performance of the four models. When sample size is small, the overall pattern does not change much (see Table 3). For some parameter estimates, the semiparametric models may slightly outperform the traditional N-N model.
| N-N model | Semi-N model | N-Semi model | Semi-Semi model | ||||||||
| AB | SE | AB | SE | AB | SE | AB | SE | ||||
| $\beta _{L}$ | -0.004 | 0.049 | -0.003 | 0.049 | -0.003 | 0.050 | -0.003 | 0.049 | |||
| $\beta _{S}$ | -0.002 | 0.017 | -0.002 | 0.017 | -0.002 | 0.017 | -0.002 | 0.017 | |||
| $\sigma _{L}^{2}$ | 0.052 | 0.090 | 0.054 | 0.090 | 0.051 | 0.090 | 0.050 | 0.089 | |||
| $\sigma _{S}^{2}$ | 0.017 | 0.009 | 0.017 | 0.009 | 0.015 | 0.009 | 0.015 | 0.009 | |||
| $\sigma _{LS}$ | -0.025 | 0.021 | -0.024 | 0.021 | -0.026 | 0.021 | -0.026 | 0.021 | |||
| $\sigma _{e}^{2}$ | -0.019 | 0.015 | -0.020 | 0.015 | -0.020 | 0.015 | -0.020 | 0.015 | |||
Note. AB: absolute bias; SE: empirical standard error.
| N-N model | Semi-N model | N-Semi model | Semi-Semi model | ||||||||
| AB | SE | AB | SE | AB | SE | AB | SE | ||||
| $\beta _{L}$ | -0.001 | 0.157 | 0.004 | 0.161 | 0.001 | 0.158 | 0.001 | 0.158 | |||
| $\beta _{S}$ | 0.007 | 0.053 | 0.005 | 0.054 | 0.006 | 0.053 | 0.006 | 0.054 | |||
| $\sigma _{L}^{2}$ | 0.025 | 0.226 | 0.029 | 0.230 | -0.016 | 0.221 | -0.021 | 0.221 | |||
| $\sigma _{S}^{2}$ | 0.039 | 0.028 | 0.037 | 0.027 | 0.019 | 0.028 | 0.018 | 0.028 | |||
| $\sigma _{LS}$ | -0.015 | 0.057 | -0.014 | 0.056 | -0.017 | 0.055 | -0.015 | 0.055 | |||
| $\sigma _{e}^{2}$ | 0.002 | 0.020 | 0.005 | 0.020 | 0.001 | 0.020 | 0.004 | 0.020 | |||
Note. AB: absolute bias; SE: empirical standard error.
Next, we evaluate the performance of the four models when data are not normally distributed. Specifically, we compare the N-N model to the Semi-N, N-Semi and Semi-Semi models in analyzing the Semi-N data, N-Semi data and Semi-Semi data, respectively. We take a close look at the parameter estimates, bias, relative bias, empirical standard errors, MSEs, and CPs.
Table 4 contains the estimation results of the N-N and Semi-N models when $N=200$, $T=3$, $C=20$, $\sigma _{LS}=0$, and $\sigma _{e}^{2}=0.5$ in analyzing the Semi-N data. When data are generated with the measurement errors coming from different clusters, using the Semi-N model consistently leads to less biased estimates, smaller standard errors and MSEs, and better CPs. For the fixed effects $\beta _{L}$ and $\beta _{S}$, estimates from the N-N model and the Semi-N model are about the same. Standard errors are smaller for the Semi-N model. Also, CPs of the 95% HPD credible intervals from the Semi-N model are relatively closer to the nominal level 95%. For parameters $\sigma _{L}^{2}$, $\sigma _{S}^{2}$, and $\sigma _{LS}$ which are related to the random effects, the bias and standard errors are uniformly smaller by fitting the Semi-N model to the data. Furthermore, the CPs for $\sigma _{S}^{2}$ and $\sigma _{LS}$ increase from 0.910 and 0.905 to 0.940 and 0.945, respectively, tending much closer to the nominal level 95%. We notice that the estimates of $\sigma _{e}^{2}$ are around 0.475 for both the N-N and Semi-N models, the standard errors are large, and the CPs are extremely different from the 95%. These are because the measurement errors $e_{it}$ are generated from $N(0,\sigma _{e}^{2})$, and $\sigma _{e}^{2}$ are generated from $IG(2,0.5)$ to control the mean of $\sigma _{e}^{2}$ to be 0.5. However, data generated from $IG(2,0.5)$ are usually less than 0.5 because this inverse Gamma distribution is skewed to the right. Therefore, in practice, we hardly can control the variance of the measurement errors when generating the Semi-N data, and thus, the bias, MSE, and CP for $\sigma _{e}^{2}$ cannot be trusted for the Semi-N data as the population parameter values are unknown. Note that the parameter estimates and their standard errors can still be trusted. For the Semi-N model, the estimated number of clusters for $\mathbf {e}_{i}$ is about 6 and the standard error of it is 0.653. There are 6 different clusters among the 200 subjects in the distribution of the measurement errors. Because we use informative priors for the DP precision parameter $\alpha $ to reduce the computational complexity and time, the estimate of $\alpha $ is very precise. The same pattern can be observed for all the other conditions in the comparison between the N-N and Semi-N models. Detailed tables under different conditions are available in Appendix A on our GitHub site: https://github.com/CynthiaXinTong/SemiparametricBayeisnGCM.
| Est. | AB | RB (%) | SE | MSE | CP | Est. | AB | RB (%) | SE | MSE | CP | ||
| $\beta _{L}$ | 6.201 | 0.001 | 0.009 | 0.082 | 0.007 | 0.960 | 6.201 | 0.001 | 0.008 | 0.081 | 0.007 | 0.955 | |
| $\beta _{S}$ | 0.303 | 0.003 | 0.845 | 0.041 | 0.002 | 0.980 | 0.302 | 0.002 | 0.620 | 0.039 | 0.001 | 0.970 | |
| $\sigma _{L}^{2}$ | 1.016 | 0.016 | 1.576 | 0.138 | 0.019 | 0.970 | 1.014 | 0.014 | 1.395 | 0.134 | 0.018 | 0.970 | |
| $\sigma _{S}^{2}$ | 0.135 | 0.035 | 35.280 | 0.035 | 0.002 | 0.910 | 0.132 | 0.032 | 31.663 | 0.028 | 0.002 | 0.940 | |
| $\sigma _{LS}$ | -0.022 | -0.022 | -2.157 | 0.058 | 0.004 | 0.905 | -0.019 | -0.019 | -1.899 | 0.053 | 0.003 | 0.945 | |
| $\sigma _{e}^{2}$ | 0.475 | -0.025 | -5.076 | 0.365 | 0.134 | 0.240 | 0.476 | -0.024 | -4.835 | 0.364 | 0.133 | 0.215 | |
| $K_{e}$ | - | - | - | - | - | - | 5.800 | - | - | 0.653 | - | - | |
| $\alpha $ | - | - | - | - | - | - | 0.999 | -0.001 | -0.069 | 0.006 | 0.000 | 1.000 | |
Note. Est.: estimate; AB: absolute bias; RB: relative bias; SE: standard error; MSE: mean square error; CP: coverage probability.
Table 5 presents the comparison between the N-N and N-Semi models when $N=200$, $T=5$, $C=20$, $\sigma _{LS}=0$, and $\sigma _{e}^{2}=0.1$ in analyzing the N-Semi data. The parameter estimates for the fixed effects $\beta _{L}$ and $\beta _{S}$ are about the same for both the N-N and N-Semi models, whereas the standard error estimates for $\beta _{L}$ and $\beta _{S}$ are smaller for the N-Semi model, usually resulting in smaller CPs of the HPD intervals. Under this specific condition, the CPs for the N-Semi model are closer to the nominal level 95%. For the variance estimate of the measurement error $\sigma _{e}^{2}$, fitting the two models leads to similar results as well. This phenomenon is closely related to the estimate of $K_{u}$. In this analysis, the estimate of $K_{u}$ is 2.418, meaning that there are only 2 potential clusters for the random effects. In this case, using the N-Semi model may not be very different from using the traditional growth curve model. For parameter $\sigma _{L}^{2}$, $\sigma _{S}^{2}$, and $\sigma _{LS}$, their bias, MSEs, and CPs cannot be trusted. The reason is similar to the reason why bias, MSE, and CP cannot be trusted for parameter $\sigma _{e}^{2}$ in analyzing the Semi-N data. Here when the N-Semi data are generated, $\mathbf {u}_{i}$ is generated from the multivariate normal distribution $MN(\mathbf {0},\boldsymbol {\Psi })$, where $\boldsymbol {\Psi =}((\sigma _{L}^{2},\sigma _{LS})',(\sigma _{LS},\sigma _{S}^{2})')$ is generated from an inverse Wishart distribution $IW(4,((1,0)',(0,0.1)'))$ to control the mean of $\boldsymbol {\Psi }$ to be $((1,0)',(0,0.1)')$. In practice, it is not possible to generate multivariate data evenly distributed around the the mean, so the population parameter values for $\boldsymbol {\Psi =}((\sigma _{L}^{2},\sigma _{LS})',(\sigma _{LS},\sigma _{S}^{2})')$ are unknown, and thus, we cannot calculate bias, MSE, and CPs for those parameters. In this analysis, we still use informative priors for the precision parameter $\alpha $ to reduce the computational time. The above pattern can be observed under the other conditions as well when comparing the N-N and N-Semi models (see detailed results in Appendix A on our GitHub site).
| N-N model | N-Semi model | ||||||||||||
| Est. | AB | RB (%) | SE | MSE | CP | Est. | AB | RB (%) | SE | MSE | CP | ||
| $\beta _{L}$ | 6.200 | 0.000 | 0.005 | 0.054 | 0.003 | 0.985 | 6.199 | -0.001 | -0.020 | 0.051 | 0.003 | 0.975 | |
| $\beta _{S}$ | 0.299 | -0.001 | -0.457 | 0.021 | 0.000 | 0.970 | 0.298 | -0.002 | -0.699 | 0.019 | 0.000 | 0.965 | |
| $\sigma _{L}^{2}$ | 0.836 | -0.164 | -16.353 | 1.304 | 1.726 | 0.120 | 0.829 | -0.171 | -17.113 | 1.299 | 1.715 | 0.050 | |
| $\sigma _{S}^{2}$ | 0.094 | -0.006 | -6.150 | 0.098 | 0.010 | 0.195 | 0.089 | -0.011 | -10.798 | 0.098 | 0.010 | 0.055 | |
| $\sigma _{LS}$ | -0.009 | -0.009 | -0.919 | 0.244 | 0.060 | 0.345 | -0.010 | -0.010 | -1.015 | 0.243 | 0.059 | 0.135 | |
| $\sigma _{e}^{2}$ | 0.099 | -0.001 | -0.529 | 0.005 | 0.000 | 0.955 | 0.099 | -0.001 | -0.737 | 0.005 | 0.000 | 0.950 | |
| $K_{u}$ | - | - | - | - | - | - | 2.418 | - | - | 0.789 | - | - | |
| $\alpha $ | - | - | - | - | - | - | 0.967 | -0.033 | -3.309 | 0.008 | 0.001 | 1.000 | |
The comparison results between the Semi-Semi and N-N models are presented in Table 6 for the Semi-Semi data when $N=50$, $T=3$, $C=20$, $\sigma _{LS}=0.3$, and $\sigma _{e}^{2}=0.5$. For this comparison, we can only compare the bias, standard error estimates, MSEs and CPs for the fixed effects parameters. Clearly, the absolute bias for the two models is close to each other, whereas the standard errors are consistently smaller for the Semi-Semi model than those for the traditional N-N model, indicating the efficiency of the estimates can be increased by using the robust Semi-Semi model. When generating the Semi-Semi data, we cannot manipulate the covariance matrix of $\mathbf {u}_{i}$ and the variance of $\mathbf {e}_{i}$ exactly. Therefore, the population parameter values of $\sigma _{L}^{2}$, $\sigma _{S}^{2}$, $\sigma _{LS}$, and $\sigma _{e}^{2}$ are unknown, so that the bias, MSEs, and CPs for these parameters cannot be evaluated. In Table 6, we also observe that the estimate of $K_{e}$ is 4.501 and the estimate of $K_{u}$ is 2.416, implying that there are about 5 clusters for $\mathbf {e}_{i}$ and 2 clusters for $\mathbf {u}_{i}$, respectively, among the 50 subjects. Different subjects’ measurement errors are distributed differently, whereas their growth trajectories are not as much different. By using the informative priors for $\alpha _{1}$ and $\alpha _{2}$, the estimates of them are very precise. More comparison results between the Semi-Semi model and the N-N model under different conditions are available in Appendix A on https://github.com/CynthiaXinTong/SemiparametricBayeisnGCM.
| N-N model | Semi-Semi model | ||||||||||||
| Est. | AB | RB (%) | SE | MSE | CP | Est. | AB | RB (%) | SE | MSE | CP | ||
| $\beta _{L}$ | 6.195 | -0.005 | -0.087 | 0.166 | 0.028 | 0.980 | 6.196 | -0.004 | -0.060 | 0.147 | 0.021 | 0.970 | |
| $\beta _{S}$ | 0.300 | 0.000 | 0.161 | 0.079 | 0.006 | 0.980 | 0.298 | -0.002 | -0.526 | 0.073 | 0.005 | 0.980 | |
| $\sigma _{L}^{2}$ | 1.098 | 0.098 | 9.841 | 1.258 | 1.592 | 0.425 | 1.051 | 0.051 | 5.126 | 1.220 | 1.491 | 0.295 | |
| $\sigma _{S}^{2}$ | 0.247 | 0.147 | 147.283 | 0.300 | 0.112 | 0.710 | 0.217 | 0.117 | 116.946 | 0.151 | 0.037 | 0.635 | |
| $\sigma _{LS}$ | 0.157 | -0.143 | -47.786 | 0.440 | 0.214 | 0.275 | 0.163 | -0.137 | -45.702 | 0.351 | 0.142 | 0.165 | |
| $\sigma _{e}^{2}$ | 0.550 | 0.050 | 10.086 | 0.907 | 0.826 | 0.285 | 0.543 | 0.043 | 8.606 | 0.959 | 0.922 | 0.230 | |
| $K_{e}$ | - | - | - | - | - | - | 4.501 | - | - | 0.420 | - | - | |
| $K_{u}$ | - | - | - | - | - | - | 2.416 | - | - | 0.584 | - | - | |
| $\alpha _{1}$ | - | - | - | - | - | - | 1.000 | 0.000 | 0.016 | 0.004 | 0.000 | 1.000 | |
| $\alpha _{2}$ | - | - | - | - | - | - | 0.980 | -0.020 | -2.007 | 0.006 | 0.000 | 1.000 | |
In sum, the performance of the four models is about the same for normally distributed data, especially when the sample size is large. When the sample size is small, even for normal data, some semiparametric models may perform slightly better than the traditional N-N model in the precision of parameter estimation. When data are not normally distributed, the traditional N-N model performs relatively worse than the semiparametric models. They may not exhibit quite different parameter estimates for fixed effects $\beta _{L}$ and $\beta _{S}$, but the standard errors for all parameters are smaller for the semiparametric models than those for the N-N model, potentially resulting in higher statistical power. In addition, the differences between the N-N model and the semiparametric models are closely related to the numbers of clusters $K_{e}$ and $K_{u}$, which represents the heteroscedasticities of $\mathbf {e}_{i}$ and $\mathbf {u}_{i}$, respectively. If $K_{e}$ or $K_{u}$ is much larger than 1, data are more likely to be nonnormal, and the differences between the results from the N-N model and the semiparametric models should be bigger. Theoretically, if the estimates of $K_{e}$ and $K_{u}$ are 1, the parameter estimation from the Semi-Semi model should be the same as those from the traditional N-N model.
We have shown that the semiparametric models perform at least equally well as the traditional N-N growth curve model when data are normal, and perform better when data are nonnormal. We recommend utilizing the semiparametric models in practical data analyses. Because there are three different semiparametric models, another purpose of this simulation study is to evaluate the effects of the misspecification of the three types of distributional growth curve models. Two commonly used statistics, which examine more than one performance criterion (Collins et al., 2001), are calculated for each model parameter to compare the three types of semiparametric growth curve models. The first statistic is the MSE based on 200 sets of parameter estimates and standard errors, and the second one is the CP of the 95% HPD credible intervals. The MSEs and CPs are then averaged over certain model parameters for each simulation condition. For the Semi-N data, MSEs and CPs are averaged over $\beta _{L}$, $\beta _{S}$, $\sigma _{L}^{2}$, $\sigma _{S}^{2}$, and $\sigma _{LS}$, because the MSE and CP for $\sigma _{e}^{2}$ cannot be trusted, as explained previously. For the N-Semi data, MSEs and CPs are averaged over $\beta _{L}$, $\beta _{S}$, and $\sigma _{e}^{2}$ since the population parameter values for $\sigma _{L}^{2}$, $\sigma _{S}^{2}$, and $\sigma _{LS}$ are unknown. For the Semi-Semi data, MSEs and CPs are only averaged over $\beta _{L}$ and $\beta _{S}$.
Table 7 summarizes the results for the analysis of each type of data by different types of distributional models with different sample sizes when $T=5$, $C=5$, $\sigma _{LS}=0$, and $\sigma _{e}^{2}=0.1$. In the table, on the rows are the different types of generated data and on the columns are the three types of semiparametric distributional models used to analyze the generated data. In almost all situations, the model used to generate the data provides the best estimation results with smaller MSE and better credible interval coverage among the three types of robust growth curve models. For example, for the Semi-N data with $N=200$, the Semi-N distributional model gives the best coverage probability and a comparable MSE to the other models. Similarly, for the N-Semi data with $N=50$, the MSE for the N-Semi model is one of the smallest and the CP for the N-Semi model is the closest to the nominal level. Intuitively, we may consider the Semi-Semi model as the most general model and apply it to all the cases. However, it is not always a good idea. First, through our simulation results, although the MSEs for the Semi-Semi model are the smallest under different conditions, the CPs for the Semi-Semi model are not always the best. By using the Semi-Semi model, the parameter estimates are slightly less accurate, while the standard errors are slightly smaller. Unexpectedly, the slight changes in the estimates and standard errors may result in a substantially lower coverage probability. Thus, the Semi-Semi distributional growth curve model is not optimal all the time. Second, theoretically, although the semiparametric approach is the same as the traditional growth curve analysis when the numbers of clusters take the value of 1, the estimated numbers of clusters are almost not possible to be 1 when we fit a semiparametric model to normal data. Because in each iteration of the MCMC sampling procedure, we count the number of clusters, which are at least 1. If in one iteration, the number of clusters happens to be bigger than 1 due to sampling errors, the estimated number of clusters cannot be exact 1. Therefore, semiparametric approach is not the same as the traditional growth curve analysis when analyzing normal data. One will lose statistical accuracy and increase type I errors by fitting the Semi-Semi distributional model to the N-N, Semi-N, or N-Semi data. Third, practically, estimating a Semi-Semi distributional model is more time-consuming than other types of models. It is often worth putting effort into determining the distributions of random effects and measurement errors to select the correct type of model.
The above results hold for different sample sizes, the number of measurement occasions, the potential number of clusters, the covariance between the latent intercept and slope, and the variance of the measurement errors. Take a closer look at the influence of these factors, we notice that the MSEs decrease as the sample size increases. By comparing Tables 7 and 8, Tables 7 and 9, Tables 7 and 10, and Tables 7 and 11, we observe separately that the number of measurement occasions, the potential number of clusters, the covariance between the latent intercept and slope, and the variance of the measurement errors do not affect the performance of the semiparametric models. More tables under different conditions are given in Appendix B on our GitHub site: https://github.com/CynthiaXinTong/SemiparametricBayeisnGCM.
| N=50 | N=200 | N=500 | ||||||||
| Semi-N | N-Semi | Semi-Semi | Semi-N | N-Semi | Semi-Semi | Semi-N | N-Semi | Semi-Semi | ||
| Semi-N | MSE | 0.016 | 0.015 | 0.015 | 0.004 | 0.004 | 0.004 | 0.002 | 0.002 | 0.002 |
| data | CP | 0.957 | 0.672 | 0.674 | 0.953 | 0.677 | 0.686 | 0.934 | 0.642 | 0.642 |
| N-Semi | MSE | 0.009 | 0.007 | 0.007 | 0.003 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 |
| data | CP | 0.892 | 0.940 | 0.885 | 0.882 | 0.943 | 0.893 | 0.903 | 0.948 | 0.907 |
| Semi-Semi | MSE | 0.013 | 0.008 | 0.008 | 0.003 | 0.002 | 0.002 | 0.001 | 0.001 | 0.001 |
| data | CP | 0.965 | 0.973 | 0.970 | 0.968 | 0.975 | 0.973 | 0.943 | 0.960 | 0.955 |
Note. MSE: mean square error; CP: coverage probability. In the table, on the rows are the different types of generated data with sample size = 50, 200, and 500. On the columns are the three types of distributional models used to analyze the generated data. For each type of the generated data, three distributional models are fitted to them. The average MSE and CP for certain model parameters are obtained, as displayed in the table.
| N=50 | N=200 | N=500 | ||||||||
| Semi-N | N-Semi | Semi-Semi | Semi-N | N-Semi | Semi-Semi | Semi-N | N-Semi | Semi-Semi | ||
| Semi-N | MSE | 0.014 | 0.014 | 0.013 | 0.004 | 0.004 | 0.004 | 0.002 | 0.002 | 0.002 |
| data | CP | 0.970 | 0.803 | 0.816 | 0.955 | 0.792 | 0.804 | 0.944 | 0.794 | 0.799 |
| N-Semi | MSE | 0.009 | 0.006 | 0.006 | 0.006 | 0.001 | 0.001 | 0.006 | 0.000 | 0.000 |
| data | CP | 0.937 | 0.958 | 0.940 | 0.900 | 0.933 | 0.915 | 0.897 | 0.927 | 0.902 |
| Semi-Semi | MSE | 0.009 | 0.007 | 0.007 | 0.003 | 0.002 | 0.002 | 0.001 | 0.001 | 0.001 |
| data | CP | 0.965 | 0.970 | 0.970 | 0.968 | 0.975 | 0.965 | 0.953 | 0.945 | 0.943 |
| N=50 | N=200 | N=500 | ||||||||
| Semi-N | N-Semi | Semi-Semi | Semi-N | N-Semi | Semi-Semi | Semi-N | N-Semi | Semi-Semi | ||
| Semi-N | MSE | 0.016 | 0.015 | 0.015 | 0.004 | 0.004 | 0.004 | 0.001 | 0.001 | 0.001 |
| data | CP | 0.950 | 0.675 | 0.684 | 0.947 | 0.683 | 0.676 | 0.944 | 0.655 | 0.659 |
| N-Semi | MSE | 0.010 | 0.005 | 0.005 | 0.034 | 0.001 | 0.001 | 0.025 | 0.001 | 0.001 |
| data | CP | 0.903 | 0.958 | 0.908 | 0.930 | 0.963 | 0.927 | 0.878 | 0.952 | 0.900 |
| Semi-Semi | MSE | 0.009 | 0.007 | 0.007 | 0.003 | 0.002 | 0.002 | 0.001 | 0.001 | 0.001 |
| data | CP | 0.978 | 0.973 | 0.978 | 0.953 | 0.958 | 0.960 | 0.960 | 0.960 | 0.963 |
| N=50 | N=200 | N=500 | ||||||||
| Semi-N | N-Semi | Semi-Semi | Semi-N | N-Semi | Semi-Semi | Semi-N | N-Semi | Semi-Semi | ||
| Semi-N | MSE | 0.017 | 0.016 | 0.016 | 0.004 | 0.012 | 0.003 | 0.002 | 0.002 | 0.002 |
| data | CP | 0.934 | 0.598 | 0.594 | 0.946 | 0.608 | 0.608 | 0.937 | 0.587 | 0.587 |
| N-Semi | MSE | 0.006 | 0.005 | 0.005 | 0.002 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 |
| data | CP | 0.877 | 0.938 | 0.877 | 0.817 | 0.913 | 0.827 | 0.752 | 0.852 | 0.737 |
| Semi-Semi | MSE | 0.010 | 0.009 | 0.008 | 0.003 | 0.002 | 0.002 | 0.001 | 0.001 | 0.001 |
| data | CP | 0.958 | 0.960 | 0.958 | 0.948 | 0.950 | 0.948 | 0.955 | 0.958 | 0.955 |
| N=50 | N=200 | N=500 | ||||||||
| Semi-N | N-Semi | Semi-Semi | Semi-N | N-Semi | Semi-Semi | Semi-N | N-Semi | Semi-Semi | ||
| Semi-N | MSE | 0.021 | 0.021 | 0.020 | 0.006 | 0.006 | 0.006 | 0.002 | 0.002 | 0.002 |
| data | CP | 0.953 | 0.845 | 0.841 | 0.939 | 0.822 | 0.819 | 0.946 | 0.833 | 0.827 |
| N-Semi | MSE | 0.018 | 0.008 | 0.008 | 0.003 | 0.002 | 0.002 | 0.002 | 0.001 | 0.001 |
| data | CP | 0.870 | 0.948 | 0.872 | 0.868 | 0.938 | 0.865 | 0.872 | 0.937 | 0.870 |
| Semi-Semi | MSE | 0.015 | 0.011 | 0.011 | 0.004 | 0.003 | 0.003 | 0.001 | 0.001 | 0.001 |
| data | CP | 0.970 | 0.968 | 0.968 | 0.948 | 0.960 | 0.953 | 0.953 | 0.960 | 0.958 |
In summary, the accuracy and efficiency of the estimation for a specific type of data closely depend on the correct specification of a model. Consequently, in practical data analyses, it is important to choose the correct type of model.
Tong & Zhang (2012) proposed three model diagnostic methods and the “distribution checking based on individual growth curve analysis” method can be easily adopted for the semiparametric approach. In this method, an individual growth curve ($\mathbf {y}{}_{i}=\boldsymbol {\Lambda }\mathbf {b}_{i}+\mathbf {e}_{i}$) is first fitted to data from each individual. Using the least square estimation method, the individual coefficients (random effects) $\mathbf {b}_{i}=(b_{iL},b_{iS})^{T}$ and the measurement errors $\mathbf {e}_{i}=(e_{i1},\ldots ,e_{iT})^{T}$ are estimated and retained. Let $\mathbf {b}=(\hat {\mathbf {b}}_{1},\cdots ,\hat {\mathbf {b}}_{N})^{T}$ and $\mathbf {e}=(\hat {\mathbf {e}}_{1},\cdots ,\hat {\mathbf {e}}_{N})^{T}$ where $\mathbf {b}$ is a $N\times 2$ matrix of individual coefficients estimates and $\mathbf {e}$ is a $N\times T$ matrix of estimated errors. Then, we test the normality of $\mathbf {e}$ and $\mathbf {b}$. If all $2$ columns of $\mathbf {b}$ follow normal distributions, we consider the individual coefficients to be normally distributed. Otherwise, we consider them nonnormally distributed. Similarly, if all $T$ columns of $\mathbf {e}$ are normally distributed, the errors are viewed as from normal distributions. If $\mathbf {e}$ and $\mathbf {b}$ are not normally distributed, semiparametric approach is recommended. Based on the combination of the distributions for $\mathbf {e}$ and $\mathbf {b}$, the decision can be made according to Table 12.
| Errors | Individual Coefficients | Model |
| normal | normal | N-N distributional model |
| nonnormal | normal | Semi-N distributional model |
| normal | nonnormal | N-Semi distributional model |
| nonnormal | nonnormal | Semi-Semi distributional model |
Restricting to a parametric probability family can delude investigators and falsely make an illusion of posterior certainty (Müller & Mitra, 2004). In this study, we proposed a semiparametric Bayesian approach for growth curve analysis with nonnormal data. The normal distributions of the random effects and/or measurement errors of traditional growth curve model were replaced by random distributions with DPM priors. Thus, four types of distributional growth curve models were discussed, including the traditional N-N model, the robust Semi-N, N-Semi, and Semi-Semi models. Through a simulation study, we systematically evaluated the performance of the semiparametric Bayesian method and further assessed the effects of the misspecification of the four types of distributional growth curve models to compare the intrinsic characteristics of them. Seven potentially influential factors were considered including type of data (N-N data, Semi-N data, N-Semi data, Semi-Semi data), type of model (N-N model, Semi-N model, N-Semi model, Semi-Semi model), number of measurement occasions ($T=3$, 5), potential number of clusters ($C=5$, 20), the covariance between the latent intercept and slope ($\sigma _{LS}=0$, 0.3), variance of measurement errors ($\sigma _{e}^{2}=0.1$, 0.3), and sample size ($N=50$, 100, 200). Among the seven factors, the number of measurement occasions, the potential number of clusters, the covariance between the latent intercept and slope, and the variance of measurement errors were not influential to the comparison among the performance of the four types of distributional models. The following conclusions can be drawn for the other three factors.
First, the three types of semiparametric models perform as well as, or better than, the traditional N-N model, especially when data are nonnormal. When data are normally distributed, we may obtain slightly biased but more efficient parameter estimates by using the semiparametric models. It is possible for the semiparametric models to lead to worse CPs, but the MSEs are often smaller. When data are nonnormal, we recommend using the robust models instead of the traditional growth curve model as they provide much more accurate and precise parameter estimates. Second, the semiparametric approach can improve the efficiency of the parameter estimation. For example, in Tables 4-6, the standard errors in the right panel are uniformly larger than those in the left panel, indicating the parameter estimation from the traditional growth curve analysis is less efficient. However, we would like to note that although the Semi-Semi model is the most general type of models, it is not always optimal. Misusing the Semi-Semi model could result in lower CPs and more type I errors. Moreover, fitting the Semi-Semi model to data is more time-consuming than fitting simpler models. Therefore, it is important to specify the correct type of model for practical data analyses. The “eyeball” method and the “distribution checking based on individual growth curve analysis” method can be used for model diagnostics (see Tong & Zhang, 2012). Third, the increase of the sample size can often improve the performance of all the four types of models. As shown in Tables 7-11, MSEs become smaller when sample size increases, but sample size does not affect the comparison among the four types of models. In general, we recommend using robust semiparametric models, especially when nonnormality is suspected.
For the semiparametric Bayesian approach, the normal assumption is replace by a random distribution with a DPM prior. In our study, the random distribution is a mixture of multivariate normal distributions with the mixing proportions generated following certain rules (e.g., truncated stick-breaking construction). So, similar to the finite growth mixture modeling, the number of clusters increases along with the increase of sample size. This is reasonable, because the diversity increases as more subjects are enrolled in the study. Naturally, there need to be more clusters. However, the semiparametric Bayesian growth curve modeling is different from finite growth mixture modeling. For finite growth mixture modeling, adding one additional cluster brings in several more parameters to be estimated. Thus, it is not possible to have many clusters when we conduct finite growth mixture analyses, whereas it is not a problem for us to obtain a large number of clusters if we use the semiparametric Bayesian method. The number of parameters for the semiparametric Bayesian model keeps the same no matter how many clusters there are.
We would like to note that the DP precision parameter $\alpha $ governs the expected number of clusters. Smaller values of $\alpha $ result in a smaller number of clusters. In this study, the DP precision parameter $\alpha $ has an informative prior $Gamma(100,100)$ to reduce the computational complexity and convergence issue. The $\alpha $s generated from the MCMC procedure are very close to 1. When $\alpha $ equals 1, about 90% prior weight on between 3 and 7 clusters (Lunn et al., 2013). Tong & Ke (2021) evaluated the effect of precision parameter prior on model estimation, model convergence, and computation time. They recommended using informative priors for the precision parameter, even when the information is inaccurate. Following their recommendation, the informative prior $Gamma(100,100)$ was chosen in this study.
In this study, we proposed to use a random mixture distribution to replace the normal assumption for robustness, but the distribution of mixture components is still specified as normal. To be more general, the distribution of mixture components can be nonnormal as well. For example, it is quite possible that the $t$ distribution is a better substitute, and the Gamma distribution probably can better accommodate the skewness in the data. Thus, the influence of the distribution form of the mixture components needs further evaluation.
Note that we only compared the parameter estimation for model comparison. How well the models fit the data is not evaluated. Deviance Information Criterion (DIC) is widely used to evaluate the model fit in Bayesian analysis. Despite the popularity of DIC, it has received much criticism since it was proposed (Spiegelhalter et al., 2002). Celeux et al. (2006) argued that the DIC introduced by Spiegelhalter et al. for model assessment and model comparison was directly inspired by linear and generalized linear models, but it was open to different possible variations in the setting of models involving random effects, as in our robust growth curve models. A number of ways of computing DICs are proposed in Celeux et al. (2006), and their advantages and disadvantages are discussed. However, the calculation of DIC in semiparametric Bayesian analysis has not been studied. Thus, a more sophisticated way to calculate DIC should be considered deeply in the future, since DIC is an important index to evaluate the model performance.
This study focuses on robust simple linear growth curve models for demonstration. However, the same methods should work for nonlinear growth curve models as well. The performance of the more complicated semiparametric growth curve models (e.g. logistic and Gompertz models) can be studied in the future.
Ansari, A. & Iyengar, R. (2006). Semiparametric Thurstonian models for recurrent choices: A Bayesian analysis. Psychometrika, 71, 631–657. DOI: https://doi.org/10.1007/s11336-006-1233-5.
Brown, E. R. & Ibrahim, J. G. (2003). A Bayesian semiparametric joint hierarchical model for longitudinal and survival data. Biometrics, 59, 221–228. DOI: https://doi.org/10.1111/1541-0420.00028.
Burr, D. & Doss, H. (2005). A Bayesian semiparametric model for random-effects meta-analysis. Journal of the American Statistical Association, 100, 242–251. DOI: https://doi.org/10.1198/016214504000001024.
Bush, C. A. & MacEachern, S. N. (1996). A semiparametric Bayesian model for randomised block designs. Biometrika, 83, 275–285. DOI: https://doi.org/10.1093/biomet/83.2.275.
Cain, M. K., Zhang, Z., & Yuan, K.-H. (2017). Univariate and multivariate skewness and kurtosis for measuring nonnormality: Prevalence, influence and estimation. Behavior Research Methods, 49, 1716–1735. DOI: https://doi.org/10.3758/s13428-016-0814-1.
Celeux, G., Forbes, F., Robert, C. P., & Titterington, D. M. (2006). Deviance information criteria for missing data models. Bayesian Analysis, 1, 651–673. DOI: https://doi.org/10.1214/06-ba122.
Collins, L., Schafer, J., & Kam, C. (2001). A comparison of inclusive and restrictive missing-data strategies in modern missing-data procedures. Psychological Methods, 6, 330–351.
Fahrmeir, L. & Raach, A. (2007). A Bayesian semiparametric latent variable model for mixed responses. Psychometrika, 72, 327–346. DOI: https://doi.org/10.1007/s11336-007-9010-7.
Ferguson, T. (1973). A Bayesian analysis of some nonparametric problems. The Annals of Statistics, 1, 209–230. DOI: https://doi.org/10.1214/aos/1176342360.
Ferguson, T. (1974). Prior distributions on spaces of probability measures. The Annals of Statistics, 2, 615–629. DOI: https://doi.org/https://doi.org/10.1214/aos/1176342752.
Ghosal, S., Ghosh, J., & Ramamoorthi, R. (1999). Posterior consistency of Dirichlet mixtures in density estimation. The Annals of Statistics, 27, 143–158. DOI: https://doi.org/https://doi.org/10.1214/aos/1018031105.
Hjort, N. L. (2003). Topics in nonparametric Bayesian statistics. In P. Green, N. L. Hjort, & S. Richardson (Eds.), Highly Structured Stochastic Systems (pp. 455–487). Oxford: Oxford University Press.
Hjort, N. L., Holmes, C., Müller, P., & Walker, S. G. (2010). Bayesian nonparametrics. Cambridge: Cambridge University Press. DOI: https://doi.org/10.1093/acprof:oso/9780199695607.003.0013.
Kleinman, K. P. & Ibrahim, J. G. (1998). A semiparametric Bayesian approach to the random effects model. Biometrics, 54, 921–938. DOI: https://doi.org/10.2307/2533846.
Lange, K. L., Little, R. J. A., & Taylor, J. M. G. (1989). Robust statistical modeling uisng the t distribution. Journal of the Americal Statistical Association, 84(408), 881–896.
Lee, S. Y., Lu, B., & Song, X. Y. (2008). Semiparametric Bayesian analysis of structural equation models with fixed covariates. Statistics in Medicine, 27, 2341–2360. DOI: https://doi.org/https://doi.org/10.1002/sim.3098.
Lu, Z. & Zhang, Z. (2014). Robust growth mixture models with non-ignorable missingness: Models, estimation, selection, and application. Computational Statistics and Data Analysis, 71, 220–240. DOI: https://doi.org/10.1016/j.csda.2013.07.036.
Lunn, D., Jackson, C., Best, N., Thomas, A., & Spiegelhalter, D. (2013). The BUGS book: A practical introduction to Bayesian analysis. Boca Raton, FL: CRC Press.
MacEachern, S. (1999). Dependent nonparametric processes. In A. S. Association (Ed.), ASA Proceedings of the Section on Bayesian Statistical Science.
Maronna, R. A., Martin, R. D., & Yohai, V. J. (2006). Robust statistics: Theory and methods. New York: John Wiley & Sons, Inc. DOI: https://doi.org/10.1002/0470010940.
McArdle, J. J. & Nesselroade, J. R. (2014). Longitudinal data analysis using structural equation models. American Psychological Association. DOI: 10.1037/14440-000.
Micceri, T. (1989). The unicorn, the normal curve, and other improbable creatures. Psychological Bulletin, 105, 156–166. DOI: https://doi.org/10.1037/0033-2909.105.1.156.
Müller, P. & Mitra, R. (2004). Bayesian nonparametric inference - why and how. Bayesian Analysis, 1, 1–33. DOI: https://doi.org/https://doi.org/10.1214/13-ba811.
Muthén, B. & Shedden, K. (1999). Finite mixture modeling with mixture outcomes using the EM algorithm. Biometrics, 55, 463–469. DOI: https://doi.org/10.1111/j.0006-341X.1999.00463.x.
Pendergast, J. F. & Broffitt, J. D. (1985). Robust estimation in growth curve models. Communications in Statistics: Theory and Methods, 14, 1919–1939. DOI: https://doi.org/https://doi.org/10.1080/03610928508829021.
Pinheiro, J. C., Liu, C., & Wu, Y. N. (2001). Efficient algorithms for robust estimation in linear mixed-effects models using the multivariate t distribution. Journal of Computational and Graphical Statistics, 10(2), 249–276.
Sethuraman, J. (1994). A constructive definition of Dirichlet priors. Statistica Sinica, 4, 639–650.
Si, Y. & Reiter, J. P. (2013). Nonparametric Bayesian multiple imputation for incomplete categorical variables in large-scale assessment surveys. Journal of Educational and Behavioral Statistics, 38, 499–521. DOI: https://doi.org/10.3102/1076998613480394.
Silvapulle, M. J. (1992). On M-methods in growth curve analysis with asymmetric errors. Journal of Statistical Planning and Inference, 32, 303–309. DOI: https://doi.org/https://doi.org/10.1016/0378-3758(92)90013-i.
Singer, J. M. & Sen, P. K. (1986). M-methods in growth curve analysis. Journal of Statistical Planning and Inference, 13, 251–261. DOI: https://doi.org/10.1016/0378-3758(86)90137-0.
Spiegelhalter, D. J., Best, N. G., Carlin, B. P., & Linde, A. v. d. (2002). Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 64(4), 583–639.
Tong, X. & Ke, Z. (2021). Assessing the impact of precision parameter prior in Bayesian nonparametric growth curve modeling. Frontiers in Psychology. DOI: https://doi.org/https://doi.org/10.3389/fpsyg.2021.624588.
Tong, X. & Zhang, Z. (2012). Diagnostics of robust growth curve modeling using Student’s t distribution. Multivariate Behavioral Research, 47, 493–518. DOI: https://doi.org/https://doi.org/10.1080/00273171.2012.692614.
Tong, X. & Zhang, Z. (2019). Robust Bayesian approaches in growth curve modeling: Using Student’s t distributions versus a semiparametric method. Structural Equation Modeling: A Multidisciplinary Journal, 27, 544–560. DOI: https://doi.org/https://doi.org/10.1080/10705511.2019.1683014.
Yang, M. & Dunson, D. B. (2010). Bayesian semiparametric structural equation models with latent variables. Psychometrika, 75, 675–693. DOI: https://doi.org/10.1007/s11336-010-9174-4.
Yuan, K.-H. & Bentler, P. M. (1998). Structural equation modeling with robust covariances. Sociological Methodology, 28, 363–396. DOI: https://doi.org/10.1111/0081-1750.00052.
Yuan, K.-H. & Bentler, P. M. (2001). Effect of outliers on estimators and tests in covariance structure analysis. British Journal of Mathematical and Statistical Psychology, 54, 161–175. DOI: https://doi.org/https://doi.org/10.1348/000711001159366.
Yuan, K.-H. & Bentler, P. M. (2002). On normal theory based inference for multilevel models with distributional violations. Pschometrika, 67, 539–561.
Yuan, K.-H. & Zhang, Z. (2012). Robust structural equation modeling with missing data and auxiliary variables. Psychometrika, 77, 803–826.
Zhang, Z. (2016). Modeling error distributions of growth curve models through Bayesian methods. Behavior Research Methods, 48, 427–444. DOI: https://doi.org/10.3758/s13428-015-0589-9.
Zhong, X. & Yuan, K.-H. (2010). Weights. In N. J. Salkind (Ed.), Encyclopedia of research design (pp. 1617–1620). Thousand Oaks, CA: Sage. DOI: https://doi.org/https://doi.org/10.4135/9781412961288.
Zhong, X. & Yuan, K.-H. (2011). Bias and efficiency in structural equation modeling: Maximum likelihood versus robust methods. Multivariate Behavioral Research, 46, 229–265. DOI: https://doi.org/https://doi.org/10.1080/00273171.2011.558736.
1 Posterior credible interval, also called credible interval or Bayesian confidence interval, is analogical to the frequentist confidence interval. The 95% HPD credible interval $[l,u]$ satisfies: 1. $Prob(l\leq \theta \leq u|data)=0.95$; 2. for $\theta _{1}\in [l,u]$ and $\theta _{2}\notin [l,u],$ $Prob(\theta _{1}|data)>Prob(\theta _{2}|data)$. In general, HPD intervals have the smallest volume in the parameter space of $\theta $, and numerical methods have to be used to find HPD intervals.