Keywords: neural networks ● machine learning ● data generating mechanisms
The nature of associations between observable variables is one of the most critical considerations for constructing theory about psychological phenomena (Borsboom, van der Maas, Dalege, Kievit, & Haig, 2020; Haslbeck, Ryan, Robinaugh, Waldorp, & Borsboom, 2019). Whether variables are associated because they all have a common cause or because they reciprocally cause and effect one another is (ideally) theorized by the researcher and (often) implied by their choice of psychometric model (Borsboom, 2006; Haslbeck, Ryan, Robinaugh, Waldorp, & Borsboom, 2019). Determining whether empirical data are generated by one of these mechanisms is therefore an important question (van Bork et al., 2019). Although other possibilities exist (Kruis & Maris, 2016; Marsman et al., 2018), these two explanations are perhaps the most common perspectives in psychology and correspond to latent variable and network models, respectively. The debate over the plausibility of these mechanisms has sparked renewed interest in the ontology and epistemology of psychological phenomena (Borsboom, 2008; Guyon, Falissard, & Kop, 2017).
Factor (latent variable) models are represented by arrows going from latent (unobservable) variables to observable variables. From a causal theory perspective, this representation suggests that a factor causes the response to the observable variables (Edwards & Bagozzi, 2000). Network models represent observable variables as nodes (circles) and their relationships (e.g., partial correlations) as edges (lines). From a causal theory perspective, this representation suggests that observed variables directly and reciprocally cause one another (van der Maas et al., 2006). For both models, researchers may not interpret the models causally but instead as summaries of covariance. In the last few years, the apparent differences between these models have been shown to be more substantive than statistical (Guyon, Falissard, & Kop, 2017), with several studies demonstrating that both models can produce similar covariance patterns and model parameters (e.g., dimensions and loadings; Golino & Epskamp, 2017; Hallquist, Wright, & Molenaar, 2019; Marsman et al., 2018; van Bork et al., 2019; Waldorp & Marsman, 2020).
Recent simulation studies, for example, have demonstrated that clusters of nodes in networks identified by community detection algorithms (Fortunato, 2010) are consistent with latent factors in factor models (Christensen, Garrido, & Golino, 2021; Golino & Epskamp, 2017; Golino et al., 2020). Other simulations have demonstrated that node strength or the absolute sum of a node’s connections in a network is consistent with confirmatory (Hallquist, Wright, & Molenaar, 2019) and exploratory factor loadings (Christensen & Golino, 2021). Despite producing similar model parameters, the substantive interpretations and representations of these models imply different data generating mechanisms. The implications of these different data generating mechanisms are important: Should a researcher use factor or network analysis to model their data? More significantly, should clinicians treat an underlying psychopathological disorder (factor model) or the symptoms that constitute the disorder (network model; Borsboom, 2017)?
To answer these questions, the present research aimed to develop an algorithm that could determine whether data were generated from a factor or network model. Such a tool allows researchers to determine whether their data are structured more like their hypothesized data generating mechanism. Although data generated from either model can fit and be represented by the other (van Bork et al., 2019; van der Maas et al., 2006), researchers should attempt to design, use, and model measures that align with their theoretical perspective (Christensen, Golino, & Silvia, 2020). Recent developments have demonstrated that factor and network models can potentially be distinguished by correlation patterns of the data (Christensen & Golino, 2021; van Bork et al., 2019). One of these methods, called the Loadings Comparison Test (LCT), compares loadings from factor and network models to predict the data-generating model (Christensen & Golino, 2021). In its current form, however, the LCT relies on descriptive heuristics, which are unlikely to generalize across many data conditions. To make the algorithm more robust, we used artificial neural networks from machine learning. We then performed a simulation to evaluate whether the neural networks perform better than the original heuristic-based algorithm and a set of regularized logistic regression models.
The LCT was inspired by van Bork et al. (2019) who demonstrated that unidimensional factor models and sparse network models have subtle statistical differences that can be used to determine whether the empirical data are more likely generated from one model or the other. In their paper, they identified two key differences: (1) the proportion of partial correlations that have a different sign than the corresponding zero-order correlations and (2) the proportion of partial correlations that are stronger than the corresponding zero-order correlations. The empirical value of these proportions is then compared against the distributions of data generated from factor and network models applied to simulated covariance matrices. The model with the greater probability is determined to be the most likely model. They referred to this test as the Partial Correlation Likelihood Test.
The Partial Correlation Likelihood Test provides a test for determining whether data are more likely generated from a factor or network model in unidimensional data structures. Although unidimensional structures are critical to psychology, the Partial Correlation Likelihood Test may not generalize to more complex models (e.g., multidimensional models; van Bork et al., 2019). The LCT was motivated by the need for such a test in multidimensional data. The development of the LCT was based on the descriptive differences between factor and network loadings when data were factor or network model (Christensen & Golino, 2021). Network loadings are the standardized sum of each node’s connections to nodes in each community in a network. Below, we provide notation for how network loadings are computed.
Let \(\textbf {W}\) represent a symmetric \(n \times n\) partial correlation network matrix where \(n\) is the number of nodes. Node strength is defined as:
\[ S_i = \sum _{j = 1}^n |\textbf {W}_{ij}| \] where \(|\textbf {W}_{ij}|\) is the absolute edge weight between node i and j and \(S_i\) is node strength for node i. Using this definition, node strength can be split by communities estimated in the network:
\[ \ell _{ic} = \sum _{j \in c}^C |\textbf {W}_{ij}|, \] where \(\ell _{ic}\) is the sum of the edge weights in community \(c\) that are connected to node i and \(C\) is the number of communities in the network. \(\ell _{ic}\) can be standardized using:
\[ \aleph _{ic} = \frac {\ell _{ic}}{\sqrt {\sum \ell _c}}, \] where \(\sqrt {\sum \ell _c}\) is the square root of the sum of all edge weights for nodes in community \(c\) and \(\aleph _{ic}\) is the standardized network loading for node i in community \(c\). Signs are added after the loadings have been computed following the same procedure as factor loadings (Comrey & Lee, 2013).
Across three simulations, Christensen and Golino (2021) demonstrated that factor and network loadings are roughly equivalent when data are generated by a factor model. To determine whether this equivalency held across other data generating mechanisms, they generated data from random correlation matrices with small correlations (between \(\pm \).15) and small-world networks. They found that factor and network loadings were no longer consistent with one another when data were generated from either data generating method. This observation led them to develop a heuristic-based algorithm (LCT) that could potentially be used to determine the data generating mechanism.
The algorithm starts by generating data from a multivariate normal distribution based on the empirical covariance matrix and estimating the number of communities (or dimensions) using exploratory graph analysis (EGA; Golino & Epskamp, 2017; Golino et al., 2020). EGA estimates a network and then applies the Walktrap community detection algorithm (Pons & Latapy, 2006) to identify the number of communities in the network (see Appendix A.1 for statistical details). Using the number of dimensions estimated by EGA, factor loadings are computed using EFA with oblimin rotation. Similarly, network loadings are computed with the EGA results. This process is repeated 100 times and loadings are computed for each generated dataset.
Next, the proportions of loadings that are greater than or equal to small, moderate, and large effect sizes are computed. For factor models, these effect sizes are 0.40, 0.55, and 0.70, respectively (Comrey & Lee, 2013). For network models, these effect sizes are 0.15, 0.25, and 0.35, respectively (Christensen & Golino, 2021). Dominant and cross-loadings that are greater than or equal to small effect sizes are also computed. The proportion of loading effect sizes are computed to summarize the covariance matrix into the same dimensions no matter how many variables are in a dataset. More specifically, any \(n \times n\) covariance matrix can be summarized by these five loadings proportions for both factor and network loadings, resulting in a comparable structure (ten loading proportions in total) for all datasets.
We summarize Christensen and Golino’s (2021) rationale for why there might be differences between factor and network models. Factor loadings are derived by extracting the common covariance between variables. This computation of factor loadings means that the magnitude of factor loadings depend on the shared variance across sets of variables. In contrast, network loadings are computed using the standardized sum of each node’s connection to nodes in a certain dimension. This computation means that their magnitudes only depend on the covariance of each node with other nodes in a dimension. When data are generated from a factor model, then there is usually common covariance to extract in each dimension. This common covariance leads factor and network loadings to be consistent with one another as Christensen and Golino (2021) demonstrate.
Data generated from network models, however, do not imply common covariance in each dimension but rather each node usually represents its own dimension (Cramer et al., 2012). Many real-world networks tend to have a small-world structure (e.g., psychopathological disorders; Borsboom, Cramer, Schmittmann, Epskamp, & Waldorp, 2011), which are characterized by nodes having many neighboring connections but also some cross-network connections with even fewer nodes that act as hubs or nodes with an above average number of connections (Watts & Strogatz, 1998). This structure suggests that there might be common covariance between variables, but they are not necessarily structured in a systematic way—that is, common covariance is not necessarily structured in well-defined dimensions like factor models. Such a structure suggests that common covariance may be identified across some variables but will be relatively diffuse in general (i.e., across factors; Christensen & Golino, 2021). In contrast, network loadings partition the covariance based on the dimension structure (rather than common covariance), leading to a greater prevalence of loadings that are likely to be at least small or larger. Finally, network loadings would also be expected to have greater proportions of cross-loadings due to the partitioning, rather than extraction, of common covariance. These differences between the two loadings may thus be informative for determining whether data were generated from a factor or network model.
The heuristics of the LCT algorithm were developed in part based on this empirical rationale as well as simulated data. The first heuristic is the ratio of small effect size (or larger) network loadings divided by small effect size (or larger) factor loadings. When this ratio is greater than 1.5, then the algorithm suggests the data are generated from a network model; if not, a second heuristic is applied. The second heuristic is the logarithm of the ratio of dominant factor loadings that are a small effect size (or larger) divided by cross-factor loadings that are a small effect size (or larger). When this logarithm ratio is greater than 5, then the algorithm suggests the data are generated from a factor model; otherwise, a network model. This latter heuristic was derived post-hoc for simulated data with large correlations between factors (0.70). Although simple, these heuristics performed remarkably well in simulated samples: 77.9% to 100% accuracy for factor models and 87.8% to 95.8% accuracy for network models (Christensen & Golino, 2021).
Despite high accuracy for all models, there were a couple limitations in their validation. First, sample sizes were all generated with 1000 cases, which is large relative to many samples used in psychology. Second, the simulated models used novel data but with the same data structures that the heuristics were derived from. The number of variables, for example, was held constant at fifteen for all models, and factor models were always generated with three factors and five variables per factor. These limitations are likely to result in overfitting and a lack of generalizability to other samples and data structures. These limitations motivated the current study where we sought to improve the LCT algorithm by replacing these simple heuristics with a more sophisticated computational approach: artificial neural networks.
Artificial neural networks are a commonly used technique in machine learning research (Dreiseitl & Ohno-Machado, 2002). They come in many forms but perhaps the most basic are feed-forward networks where data are input as nodes and are “fed through” the network to output nodes (i.e., the prediction). In machine learning terms, neural networks are a supervised learning model, which means that the researcher supplies both the input variables and the output variables that the neural network must then “learn” a mapping between them. In our study, the input corresponded to the factor and network loading proportions. The output corresponded to the data-generating model (either factor or network). The mapping between the input and output occurs through the hidden layers of the neural network where the model learns the appropriate weighting scheme that optimizes the prediction of the output from the input.
A neural network with no hidden layers can represent linear functions only and is equivalent to a standard regression model (e.g., an output node with a sigmoid activation function is a logistic regression model). With a single hidden layer, a neural network can approximate “any function that has a continuous mapping from one finite space to another” (Heaton, 2008). Two hidden layers can represent any arbitrary boundary (e.g., non-linear functions), approximating any mapping between the input and output (Hornik, 1991; Sontag, 1991). Key to training neural networks is deciding on the number of hidden layers and the number of neurons (or nodes) in each of the hidden layers. More complex mappings require more complex neural networks (i.e., more nodes and layers).
An important concept for neural network learning is backpropogation. Backpropogation refers to the adjustment of weights and biases in the network (starting from the output back to the input; Watt, Borhani, & Katsaggelos, 2016). In training, batches or a certain number of samples of the data are fed through the network’s weights and predictions are made about the output. With each batch, the network updates its weights and biases by trying to minimize the loss of information between the predicted output and the actual output. The end goal is to minimize the loss of information between the predicted and actual output to maximize the accuracy of the neural network’s predictions.
One of the advantages of neural networks is that they can learn mappings between the input and output that are otherwise difficult to abstract (e.g., non-linear relationships). In our case, going beyond simple descriptive heuristics to map loading proportions to the data-generating model. This advantage of neural networks is also a disadvantage. The mapping is often a “black box” that does not offer clear interpretations of the underlying function—that is, what exactly the neural network is using to distinguish a factor model from a network model.
In this section, we briefly describe the training procedure we used to arrive at our final neural networks (a full description of the training process can be found in Appendix A.2). Based on the original LCT algorithm, we expected certain conditions to be more difficult to predict the data-generating model. Specifically, we expected the size of the correlation between factors to have a substantial effect on prediction accuracy. To this end, we started by training two neural network models: one with low correlations between factors (0.00 and 0.30) and another with high correlations between factors (0.50 and 0.70). Such a strategy is often referred to as an ensemble of networks (Zhou, Wu, & Tang, 2002) where each network is fine-tuned to a specific part of the problem to improve the overall prediction of a more complex problem. The rationale for building several neural networks to predict different factor models from network models is that different information is likely to be more relevant for one set of factor models than another (primarily along the lines of the magnitude of correlations between factors).
During the training of neural networks, part of the data is “held out” from the network’s learning. Consistent with the literature, we used an 80/20 split of our data where 80% of the data is used to train the network and 20% of the data is used to validate the training. The purpose of this procedure is to evaluate the neural network on data that was not used in its training. During this procedure, we found that the high correlations between factors neural network was not very accurate. We discovered that there were specific conditions where the neural network was unable to predict the data-generating model. These conditions were where the number of variables per factor was greater than the number of factors. Based on this finding, we used two neural networks for factor models with high correlations between factors (0.50 and 0.70): one with the number of variables per factor greater than the number of factors and another with the number of variables per factor less than the number of factors. The training validation accuracy of both neural networks was sufficient.
Our final neural network ensemble consisted of three neural networks: low correlations between factors, high correlations between factors with the number of variables per factor greater than the number of factors, and high correlations between factors with the number of variables per factor less than the number of factors. Our ensemble worked by having each neural network make a prediction for whether the data were generated from a factor or network model. If any of the neural networks predicted a factor model, then the ensemble suggests a factor model. Conversely, if all neural networks predicted a network model, then the ensemble suggests a network model. To determine whether a neural network approach was necessary, we compared their performance to corresponding logistic regression models that were regularized using the least absolute shrinkage and selection operator (LASSO; Tibshirani, 1996). Logistic regression is commonly used as a comparison method and is useful for determining the expected baseline performance of a neural network (Dreiseitl & Ohno-Machado, 2002).
In our present study, we set out to validate the neural networks against Christensen and Golino’s (2021) original LCT heuristics and the logistic regression models that were trained alongside the neural networks. Although the neural networks were already validated on novel samples held out from their training samples, we sought to further test their generalizability by generating data using different conditions than the ones they were trained on—that is, manipulating the parameters of the factor and network models such that they were novel. Further, we generated data from random network models, which were not used to train the neural network and logistic regression models or the development of the original heuristic-based algorithm. Random network models are generated by a random process, making dependencies between variables unsystematic. Because the random network models are completely novel, they represent an ideal test of generalizability.
The original algorithm relied on a bootstrap approach (e.g., generating 100 samples) to compute the loadings proportion heuristics used to predict the model. In contrast, the neural network and logistic regression approaches can make predictions based on the empirical data. One potential advantage of the neural network and logistic regression approaches is that they can also be applied to each sample of the bootstrap data. Beyond the empirical predictions, the means of the loadings proportions could be computed and used to make a prediction. Another prediction could made based on the proportion of each time a model was predicted from the data (e.g., more than 50% of the samples suggesting a model predicts that model). In our simulation, we tested each type of prediction (hereafter referred to as empirical, bootstrap, and proportion, respectively).
All data were generated as continuous variables and sample sizes for all models were generated with 400 and 750 cases. For each model, a total of 7,200 samples were generated, resulting in 21,600 total samples. Conditions of each model consisted of different parameter settings than what the neural network and logistic regression models were trained on. The random network models were completely novel to all LCT configurations.
We generated data from multivariate normal factor models following the same approach as Golino et al. (2020). First, the reproduced population correlation matrix was computed:
\[\mathbf {R_R} = \mathbf {\Lambda \Phi \Lambda }',\] where \(\mathbf {R_R}\) is the reproduced population correlation matrix, \(\mathbf {\Lambda }\) is the \(k\) (variables) × \(r\) (factors) factor loading matrix, and \(\mathbf {\Phi }\) is the \(r\) × \(r\) correlation matrix. The population correlation matrix, \(\mathbf {R_P}\), was then obtained by putting the unities on the diagonal of \(\mathbf {R_R}\). Next, Cholesky decomposition was performed on the correlation matrix such that:
\[\mathbf {R_P} = \mathbf {U}'\mathbf {U}.\]
If the population correlation matrix was not positive definite (i.e., at least one eigenvalue \(\le \) 0) or any single item’s communality was greater than 0.90, then \(\mathbf {\Lambda }\) was re-generated and the same procedure was followed until these criteria are met. Finally, the sample data matrix of continuous variables was computed:
\[\mathbf {X} = \mathbf {ZU},\] where \(\mathbf {Z}\) is a matrix of random multivariate normal data with rows equal to the sample size and columns equal to the number of variables.
We manipulated number of variables per factor (4, 6, and 8), number of factors (2, 4, and 6), and correlations between factors (.00, .30, .50, and .70). As the magnitude of the correlations between factors increased, so too did the variance of the distribution the cross-loadings were drawn from. Specifically, cross-loadings were drawn from a random normal distribution with a mean of 0 and standard deviation of .050, .075, .100, and .125, respectively. This made it possible to generate cross-loading magnitudes that were quite large (e.g., .40), creating more difficult conditions to decipher factor from network models when the correlations between factors were large (e.g., .70). Cross-loadings were allowed to be both positive and negative. Factor loadings on the dominant factors were randomly drawn from a uniform distribution with a minimum of .40 and maximum of .70. In total, there were 72 conditions (sample size \(\times \) number of factors \(\times \) variables per factor \(\times \) correlations between factors) that were generated 100 times.
We generated data from two different network models: small-world and random. We generated small-world networks by adapting the bdgraph.sim algorithm in the BDgraph package (Mohammadi & Wit, 2015) in R (R Core Team, 2020) to incorporate the sample_smallworld function from the igraph package (Csardi & Nepusz, 2006). The algorithm starts by generating a binary undirected small-world network that follows the Watts-Strogatz model (Watts & Strogatz, 1998). Next, following Williams, Rhemtulla, Wysocki, and Rast (2019), the weights are drawn from a G-Wishart distribution corresponding to 90% of partial correlations within the range \(\pm \).40. As Williams, Rhemtulla, Wysocki, and Rast (2019) note, large networks are more likely to have smaller partial correlations due to more variance being partialled out; however, given that many psychological assessment instruments have redundancies (Christensen, Golino, & Silvia, 2020), partial correlations as large as .40 may not be uncommon even when there are a large number of variables (Wysocki & Rhemtulla, 2019). Therefore, we allowed networks, regardless of the number of variables, to have weights between \(\pm \).40. The distributions of the absolute values of these weights were typically positively skewed.
For the small-world network models, number of variables (12, 24, 36, and 48), rewiring probabilities (.075, .15, and .30), and densities (.30, .50, and .70) were manipulated. The rewiring probabilities were chosen on the basis of typical small-world network models where the standard Watts-Strogatz small-world model is around .10 (\(\pm 5\)) and typical psychological small-world networks are likely somewhere between .01 and .50. Importantly, the number of variables tended to be within the same range as the factor models (between 8–48) to allow for closer comparisons of the two models, which had a similar number of variables. It is worth noting that our density and partial correlation magnitudes were within the general range of many psychological networks (for a review, see Wysocki & Rhemtulla, 2019). In total, there were 72 conditions (sample size \(\times \) number of variables \(\times \) rewiring probabilities \(\times \) densities) that were generated 100 times.
We generated random networks using the bdgraph.sim algorithm in the BDgraph package. The network and data generation approach was identical to the small-world networks. The main difference is that random networks randomly connect edges between all nodes, making them less structured relative to small-world networks (Watts & Strogatz, 1998). Like the small-world networks, we manipulated the number of variables (15, 25, 35, and 45) and density of the random networks (.30, .50, and .70). We also manipulated the probability that a pair of nodes would have edge (.25, .50, .75). In total, there were 72 conditions (sample size \(\times \) number of variables \(\times \) rewiring probabilities \(\times \) densities) that were generated 100 times.
We computed analysis of variances (ANOVAs) across conditions. We used a fully factorial design to allow for all possible interactions between conditions. Partial eta squared (\(\eta _p^2\)) was used for effect size. We followed Cohen’s (1992) effect size guidelines: small (\(\eta _p^2 = 0.01\)), moderate(\(\eta _p^2 = 0.06\)), and large (\(\eta _p^2 = 0.14\)).
We computed confusion matrix metrics for the models using the empirical, bootstrap, and proportion predictions of the algorithm. To provide an example of these metrics, we use the factor model as the model under consideration. A true positive (TP) was when the predicted and true generating model matched the model under consideration (e.g., factor). A true negative (TN) was when the predicted and true generating model (e.g., network) were not the model under consideration (e.g., factor). A false positive (FP) was when the predicted generating model matched the model under consideration (e.g., factor) but not the true generating model (e.g., network). A false negative (FN) was when the predicted generating model (e.g., network) did not match the model true generating model and model under consideration (e.g., factor).
Using this confusion matrix, we computed sensitivity (\(\frac {TP}{TP + FN}\)), specificity (\(\frac {TN}{TN + FP}\)), false discovery rate (FDR; \(\frac {FP}{FP + TP}\)), accuracy (\(\frac {TP + TN}{TP + FP + TN + FN}\)), and Matthews correlation coefficient (MCC; \(\frac {(TP \times TN) - (FP \times FN)}{\sqrt {(TP + FP) \times (TP + FN) \times (TN + FP) \times (TN + FN)}}\)). Sensitivity is the proportion of positives that are correctly identified as TPs, while specificity is the proportion of negatives that are correctly identified as TNs. The FDR is the proportion of FPs that are found relative to the total positives that are predicted by the algorithm. Accuracy is the proportion of correct predictions (TPs and TNs) of the algorithm, representing an overall summary of sensitivity and specificity. Finally, the MCC is considered the best overall metric for classification evaluation because it is an unbiased measure that uses all aspects of the confusion matrix, representing a special case of the phi coefficient between the predicted and true model (Chicco & Jurman, 2020).
Starting with general accuracy, the neural network predictions had the highest percent correct: proportion (96.2%), bootstrap (95.1%), and empirical (86.7%). These were followed by the original algorithm (85.9%) and the logistic regression predictions: bootstrap (70.5%), proportion (68.7%), and empirical (67.4%). Because the logistic regression predictions were poor, we focus on the confusion matrix metrics of the neural network and original algorithm predictions.
Across all metrics, the bootstrap and proportion predictions were superior to the single-shot empirical predictions. It is important to note that accuracy and MCC will be the same between models, specificity and sensitivity will be the opposite between models, and FDR will be different between the two models. For specificity and sensitivity, we focus on factor models (sensitivity and specificity for network models, respectively). Overall, proportion predictions outperformed all others: sensitivity = 0.995 and specificity = 0.946 for factor models. The accuracy and MCC were also very high: 0.962 and 0.919, respectively. The FDR was 0.099 for factor models and 0.003 for network models.
The bootstrap predictions performed similarly well: sensitivity = 0.987 and specificity = 0.933 for factor models. The accuracy and MCC were high: 0.951 and 0.896, respectively. The FDR was 0.120 for factor models and 0.007 for network models. The empirical predictions were slightly better than the original algorithm (in parentheses): sensitivity = 0.984 (0.931) and specificity = 0.809 (0.822) for factor models. The accuracy and MCC were fairly high: 0.867 (0.859) and 0.751 (0.718), respectively. The FDR was 0.279 (0.273) for factor models and 0.010 (0.041) for network models.
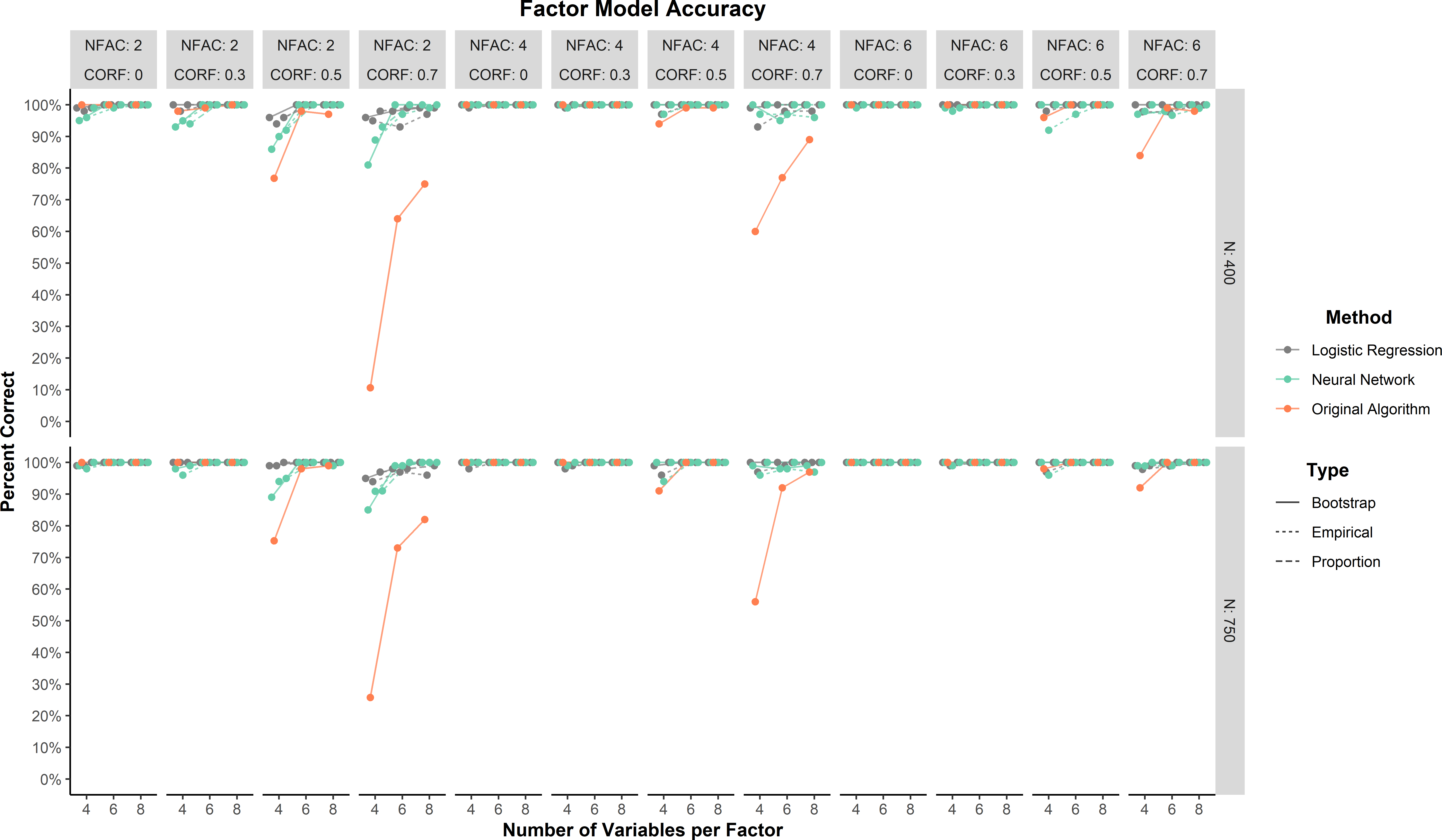
In general, predictions for the factor model were highly accurate (\(\ge \) 75%) across all conditions for the neural network and logistic regression methods (Figure 1). Lower accuracy for all methods tended to occur when correlations between factors were large (.70). The ANOVA found that there was only one effect that reached at least a moderate effect size. This moderate effect was an interaction between method and correlations between factors (\(\eta _p^2 = 0.07\)). This interaction was driven by the original algorithm and large correlations between factors (Figure 1).

Across all conditions, the neural network and logistic regression methods were comparable to or better than the original LCT algorithm. The neural network method was comparable to logistic regression method on all three prediction types: empirical (98.4% and 98.9%, respectively), bootstrap (98.7% and 99.6%, respectively), and proportion (99.5% and 99.8%). The original algorithm was lower but still had high accuracy (93.1%).
As a general trend, all methods tended to improve in percent correct as the small-world network models became denser (Figure 2). The neural network method by far outperformed the logistic regression and original algorithm methods when the networks were sparse (0.30). Across all conditions, the neural networks performed as well as or better than the logistic regression and original algorithm predictions, with the proportion predictions achieving at least 75% correct or greater. There was one large effect for method (\(\eta _p^2 = 0.18\)). The overall percent correct made this effect clear: neural network (90.9%), logistic regression (82.1%), and original algorithm (56.5%).
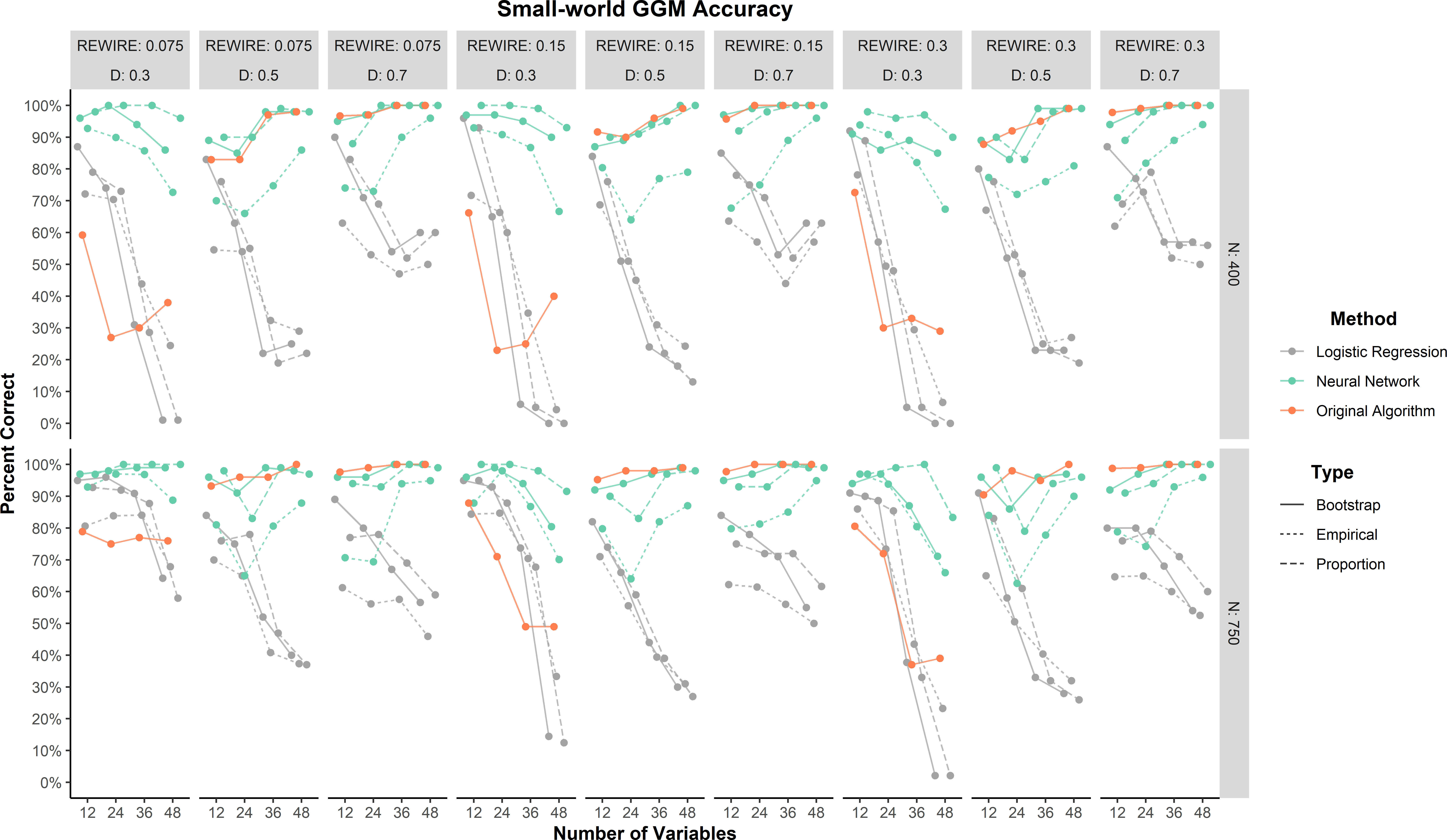
Relative to the neural network method, the logistic regression and original algorithm methods did not perform as well. These results suggest that the logistic regression and original algorithm were strongly biased toward factor models. There were two clear patterns in their results. Logistic regression performed worse as the density decreased and the number of variables increased. The original algorithm was primarily affected by density with accuracy decreasing as density decreased.
The random network models were not used to train or develop the methods and therefore represent the strongest test of generalizability. As a general trend, all methods tended to improve in percent correct as the random network models became denser (Figure 3). Overall, the neural network (88.3%) outperformed the original algorithm (82.3%) and logistic regression (50.8%) methods. When broken down by prediction type, neural network proportion (93.4%) and bootstrap (91.8%) predictions had the highest accuracy followed by the original algorithm (82.3%) and neural network empirical (79.6%) prediction. All logistic regression predictions were less than 60%. There was one large effect for method (\(\eta _p^2 = 0.20\)). This effect was largely driven by logistic regression (Figure 3).
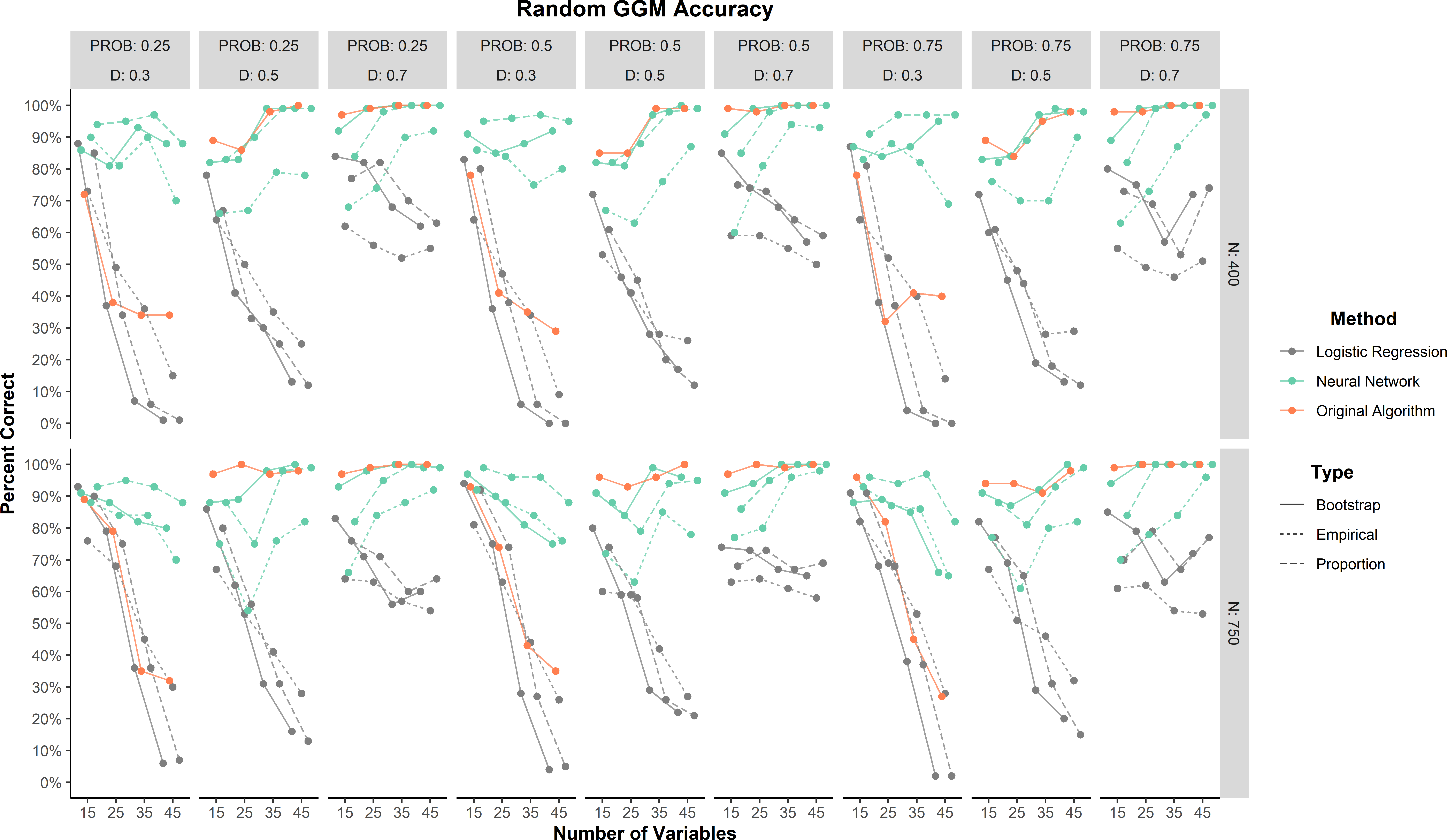
These results add further support to the finding that logistic regression was strongly biased toward factor models. Similar to the small-world network results, all methods tended to decrease in accuracy as the density decreased. Accuracy tended to increase as variables increased for the neural network while accuracy tended to decrease as variables increased for logistic regression.
The simulation provides evidence that the LCT algorithm paired with neural networks can be a powerful predictive tool for identifying whether data are generated from a specific model. It is important, however, to demonstrate that the LCT works in practice. To illustrate this, we examined two different datasets that are assumed to be generated from a factor and network model.
The first example dataset consisted of 2800 observations on items from the International Personality Item Pool’s (Goldberg, 1999) Big Five Inventory (BFI; John, Donahue, & Kentle, 1991), which is available in the psych package (Revelle, 2017) in R. The BFI traditionally has five factors, each with five items, corresponding to the Big Five factor model: openness to experience, conscientiousness, extraversion, agreeableness, and neuroticism. The robustness of this factor structure has been demonstrated across a variety of samples (e.g., Donnellan, Oswald, Baird, & Lucas, 2006). Although there is no way to determine that the BFI is actually generated from a factor model, its robust factor structure suggests that the data structure should follow a factor model.
We applied the LCT to the full dataset as well as sub-samples that were randomly split into 400 cases each (seven sub-samples in total; see Appendix A3 for code to replicate this analysis). For the full dataset, all predictions—empirical, bootstrap, and proportion—were for a factor model. Across the sub-samples, the results varied slightly by prediction: empirical (6 factor and 1 network), bootstrap (7 factor), and proportion (7 factor).
The second example dataset consisted of mean blood oxygen level-dependent (BOLD) activation levels of twenty regions of interest (ROIs) in the brain that corresponded to the default mode network (DMN) during five-minute resting state scans in 144 participants from Beaty et al. (2018). The DMN corresponds to a set of cortical midline, medial temporal, and posterior inferior parietal regions that often co-activate together. Recent research has demonstrated that the DMN can be broken down into several distinct sub-networks (Andrews-Hanna, Smallwood, & Spreng, 2014; Gordon et al., 2020). Brain networks are a well-known real-world example of networks, which make them an appropriate test of whether the LCT performs as expected.
We applied the LCT to the correlation matrices of the 20 ROIs based on the DMN structure identified in the Shen brain atlas (Shen, Tokoglu, Papademetris, & Constable, 2013; see Appendix A.4 for code to replicate this analysis). The correlation matrices were derived from time series with the length of 150, which was used as the sample size input for the LCT. For the bootstrap and proportion predictions, all participants’ DMN networks were suggested to be generated from a network model. The empirical prediction suggested that most 140 (97.2%) were generated from network models.
Taken together, these examples demonstrate the validity of the LCT on real-world datasets that were expected to be generated from factor and network models. Given the robustness of the proportion prediction of the LCT in the simulation and our examples here, we suggest that researchers should place the most weight on this prediction. A consensus across predictions is most likely to be robust but when they conflict researchers should give priority to the proportion prediction followed by the bootstrap and empirical predictions. One benefit of the proportion prediction is that it provides some inference into the certainty of the data-generating model by offering the proportion of samples that were predicted to be from either a factor or network model.
The present study sought to use artificial neural networks to improve the LCT algorithm, which was designed to determine whether data are generated from a factor or network model based on factor and network loading structures. Our results demonstrate how artificial neural networks can be a powerful tool for developing highly predictive models. In the context of our study, we demonstrated that neural networks (specifically with proportion predictions) outperform simple heuristics (i.e., the original LCT algorithm) and logistic regression models for predicting the data-generating model.
The significance of this problem has grown increasingly relevant as recent studies have demonstrated that similar covariance patterns and models parameters (e.g., dimensions, loadings) can be derived from factor and network models (Golino et al., 2020; Hallquist, Wright, & Molenaar, 2019; Marsman et al., 2018; van Bork et al., 2019; Waldorp & Marsman, 2020). These findings have shifted the focus of the differences between these models from statistical to theoretical (Guyon, Falissard, & Kop, 2017; Kruis & Maris, 2016). Indeed, when the data generating mechanism is a factor model, then the model parameters of factor and network models can be shown to be consistent with one another (e.g., dimensions, loadings; Christensen & Golino, 2021; Golino et al., 2020). These parameters, specifically loadings, start to differ when the data generating mechanism is not a factor model. This raises an important question: What is the difference between the structure of factor and network models?
We pinned our rationale on the factor model’s focus on extracting common covariance. When it comes to our neural networks, their interpretations are a black box of linear and non-linear transformations of the input to the output and therefore make our predictions accurate but not necessarily explanatory (but see Buhrmester, Müch, & Arens, 2019; Yarkoni & Westfall, 2017). Although some hints are provided by our feature importance analysis (see Appendix A.2), the exact mapping of between the loading structures and predicted model is likely multifaceted (as demonstrated by the better performance in training and validation of the neural networks over logistic regression). In unidimensional models, there appears to be some statistical differences that can be exploited but this may not generalize to more complex models (van Bork et al., 2019). We show that, at the very, least summaries of the data’s structure (proportions of small, dominant, and cross-loadings) are important for differentiating data generated from these models.
When considering statistical assumptions and the feature importance analysis, our results point to the cross-loadings between dimensions: factor models tend to minimize cross-loadings whereas network models typically have many (Christensen & Golino, 2021). Indeed, cross-loadings of the factor models were either the first or second most important input for the neural networks predicting whether the data were generated from a factor or network model (see Appendix A.2). Another difference is the extent to which there is clustering due to common covariance: factor models attempt to specifically extract common covariance whereas network models partition covariance. This is made evident by the importance of the dominant factor loading across the models. This strongly suggests that the lack of common covariance in dimensions of network models is a substantial contributor for differentiating them from factor models. This finding is consistent with variables in network models being characterized as “causally autonomous” (Cramer et al., 2012).
Although our findings may not be able to provide an exact statistical answer about the differences between these models (e.g., van Bork et al., 2019), they do provide a predictive tool for whether data are structured as a factor or network model. Specifically, the proportion predictions of the neural network following the LCT algorithm had high accuracy for all models. Importantly, we do not suggest that the LCT can inform the researcher about whether their data was actually generated from a specific model. This is a critical distinction: The LCT can accurately predict whether the data are structured as a specific model rather than actually being generated by it. Indeed, our simulated data were generated from specific models but this does not mean that data structured like a factor model could not be generated from a network model (and vice versa; Fried, 2020; van Bork et al., 2019; van der Maas et al., 2006).
This issue of equally plausible data-generating mechanisms has been discussed at length in the literature (Christensen & Golino, 2021; Marsman et al., 2018; van Bork et al., 2019; Waldorp & Marsman, 2020), leading to recent calls for researchers to develop formal (i.e., computational and mathematical) theories about their psychological phenomena of interest (Borsboom, van der Maas, Dalege, Kievit, & Haig, 2020; Fried, 2020; Haslbeck, Ryan, Robinaugh, Waldorp, & Borsboom, 2019). Theories and hypotheses about the relations between components of the phenomena should be developed a priori to test their relations. These should then inform whether a factor or network model is a more appropriate statistical model for the representation of those relations. We view the LCT as a test for whether components are structured like a factor or network model, which can inform the researcher as to whether the relations between components are interacting as expected. Said differently, we do not advise that the LCT supplant theory about the relations between variables but suggest that it can serve as a tool for reasoning about the hypothesized structure of psychological measurements.
In this respect, scale developers can structure their scales to align more with the structure of a factor or network model—that is, the data structure can be manipulated to produce data that appear to be generated from one model or the other (see Appendix A.6 for an example). In fact, contemporary psychometric practice has been doing exactly this for many years: variables that are strongly interrelated are usually retained in scales and variables with substantial cross-loadings are usually removed from scales (DeVellis, 2017). This approach is often justified to ensure that the phenomena of interest are being cleanly measured (i.e., unidimensional) yet most researchers rarely discuss whether the theory about the relations between the variables actually dictate such distinctions. Therefore, it again comes down to theory as to whether the data are actually generated from said model.
For more practical terms, researchers must consider the data-generating model when estimating scores from these psychometric models (network scores can be computed as a weighted composite; e.g., Golino, Christensen, Moulder, Kim, & Boker, 2020). As shown in Appendix A.2 and Christensen and Golino (2021), the loading structures for factor and network loadings are consistent with one another when the data are generated from a factor model, which suggests that there is little consequence in whether a factor or network model is used to estimate scores (Golino, Christensen, Moulder, Kim, & Boker, 2020). When the data are generated (or even structured) as a network model, then there is divergence between the loading structures with variables (e.g., dominant loadings; Appendix A.2). This divergence can have a substantial effect on the computation and interpretation of scores.
Such a consequence has been noted in less drastic circumstances with sum scores and factor scores where differences can be observed when a tau-equivalent latent variable model (i.e., sum scores) is applied to data generated from a congeneric latent variable model (i.e., factor scores; McNeish & Wolf, 2020). These differences in factor structures can potentially have substantial consequences for the reliability and validity of measurement. Moreover, these consequences further underscore the importance for researchers to consider that “scoring scales—by any method—is a statistical procedure that requires evidence and justification” (McNeish & Wolf, 2020, p. 2). Therefore, if data are generated from a network model, then factor scores may not be appropriate and could possibly jeopardize the validity of the research. Our study demonstrates that the LCT can be used as one method to provide such evidence and justification as well as guide researchers toward more valid measurement.
Importantly, we also echo recent calls by researchers who have stated that there is no need to pit these models against each other but rather develop hybrid models that include components that are from common cause and causal systems (Christensen, Golino, & Silvia, 2020; Epskamp, Rhemtulla, & Borsboom, 2017; Fried, 2020; Guyon, Falissard, & Kop, 2017). In this way, researchers should consider the level of organization at which each phenomena is being measured. Factor models, for example, may be more appropriate when measuring a specific phenomenon with highly similar variables like a single characteristic of personality whereas network models may be more appropriate for understanding how these specific characteristics coalesce into more complex systems like a personality trait (Christensen, Golino, & Silvia, 2020; Mõtus & Allerhand, 2017). Even still, individual personality traits may then appear as a factor model when examined together. This suggests that the level of organization may influence the data structure and the relationships between the psychological components. This jibes with the notion that hybrid models may be the most optimal stance (Fried, 2020; Guyon, Falissard, & Kop, 2017). The LCT can help researchers explore and verify these hypothesized structures to better determine how hybridization should occur.
There are several limitations that researchers must consider when using the LCT. First, the LCT was trained on small-world network models and therefore carries the assumption that most psychological networks will be generated from small-world network models. We think this assumption is reasonable because many real-world networks show small-world structure (e.g., brain networks; Muldoon, Bridgeford, & Bassett, 2016) and many psychological phenomena exhibit properties that align with these assumptions such as psychopathological disorders (Borsboom, Cramer, Schmittmann, Epskamp, & Waldorp, 2011): clustering of symptoms within a disorder (high clustering coefficient) yet bridges between symptoms to other disorders (low average shortest path lengths; Cramer, Waldrop, van der Maas, & Borsboom, 2010). Moreover, we demonstrate that the LCT can generalize to random network structures, which may be more appropriate when the network consists of unique variables that represent a specific dimension like a network comprised of individual latent variables that represent causally distinct phenomena (Cramer et al., 2012).
There are few standards for the characteristics and topology of what can be considered a “typical” psychological network. Our data generating assumptions were based on previous evidence that most real-world networks tend to be small-world (including psychological networks; Borsboom, Cramer, Schmittmann, Epskamp, & Waldorp, 2011), but the extent to which psychological networks are represented by small-world networks and whether the parameters used in the study mimic real-world psychological networks requires empirical validation (but see Wysocki & Rhemtulla, 2019). In large part, this is because few psychological network studies have examined the topological features of psychological networks such as their degree distribution, which is a critical characteristic for determining the type of network (e.g., random, small-world, scale-free, exponential random graph; Newman, 2010). Further, small-worldness measures should be used to determine whether data are more like a random, lattice, or small-world network (see Telesford, Joyce, Hayasaka, Burdette, & Laurienti, 2011). In practice, this task is difficult because network estimation methods differ in their preference for sparsity, which affects all network measures (Wysocki & Rhemtulla, 2019). Better data generation follows from more studies examining and reporting the topology of psychological networks (e.g., Battiston et al., 2020; Burger et al., 2020), which can in turn be used to train better neural networks to make more valid predictions.
This leads us to a second, influential limitation: the predictions of the neural networks are only as good as the data they are trained on. Therefore, we must be critical of our own data generating methods and question whether they resemble real-world data. We believe that we have provided reasonably realistic datasets that include factor models with dominant loadings between .40 and .70 and a varying degree of cross-loadings. The range of loadings represent what are considered to be acceptable to very high (Comrey & Lee, 2013), with .40 being considered a rule of thumb for appropriate measurement of a latent variable (DeVellis, 2017). Still, not all datasets will have loadings on the dominant factor that are within this range.
Finally, in light of our discussion on theory, the LCT is focused on cross-sectional datasets when most phenomena are likely to be dynamical systems (e.g., Haslbeck, Ryan, Robinaugh, Waldorp, & Borsboom, 2019). This is a limitation of the current implementation of the LCT but we suspect that the LCT can be generalized to time series data by using dynamic factor analysis and dynamic EGA (Golino, Christensen, Moulder, Kim, & Boker, 2020). Such an approach could lead to determining whether some people represent represent a phenomenon of interest as a common cause or causal system. This in turn could offer inferences into individualized psychopathological intervention (Wright & Woods, 2020), providing more specific answers to whether it would be more effective for a clinician to treat an underlying disorder or specific symptoms.
All data, code, and materials can be found on the Open Science Framework: https://osf.io/4fe9g/.
The authors made the following contributions. Alexander P. Christensen (https://orcid.org/0000-0002-9798-7037): Conceptualization, Software, Methdology, Writing - Original Draft, Writing - Review & Editing; Hudson Golino (https://orcid.org/0000-0002-1601-1447): Conceptualization, Software, Methdology, Writing - Review & Editing.
Correspondence concerning this article should be addressed to Alexander P. Christensen, Department of Neurology, University of Pennsylvania, Philadelphia, PA, 19104. E-mail: alexpaulchristensen@gmail.com
Allaire, J. J., & Chollet, F. (2020). keras: R interface to ‘Keras’. Retrieved from https://keras.rstudio.com
Andrews-Hanna, J. R., Smallwood, J., & Spreng, R. N. (2014). The default network and self-generated thought: Component processes, dynamic control, and clinical relevance. Annals of the New York Academy of Sciences, 1316, 29–52. doi: https://doi.org/10.1111/nyas.12360
Battiston, F., Cencetti, G., Iacopini, I., Latora, V., Lucas, M., Patania, A., … Petri, G. (2020). Networks beyond pairwise interactions: Structure and dynamics. Physics Reports. doi: https://doi.org/10.1016/j.physrep.2020.05.004
Beaty, R. E., Kenett, Y. N., Christensen, A. P., Rosenberg, M. D., Benedek, M., Chen, Q., … Silvia, P. J. (2018). Robust prediction of individual creative ability from brain functional connectivity. Proceedings of the National Academy of Sciences, 115, 1087–1092. doi: https://doi.org/10.1073/pnas.1713532115
Borsboom, D. (2006). The attack of the psychometricians. Psychometrika, 71, 425–440. doi: https://doi.org/10.1007/s11336-006-1447-6
Borsboom, D. (2008). Psychometric perspectives on diagnostic systems. Journal of Clinical Psychology, 64, 1089–1108. doi: https://doi.org/10.1002/jclp.20503
Borsboom, D. (2017). A network theory of mental disorders. World Psychiatry, 16, 5–13. doi: https://doi.org/10.1002/wps.20375
Borsboom, D., Cramer, A. O. J., Schmittmann, V. D., Epskamp, S., & Waldorp, L. J. (2011). The small world of psychopathology. PLoS ONE, 6, e27407. doi: https://doi.org/10.1371/journal.pone.0027407
Borsboom, D., van der Maas, H., Dalege, J., Kievit, R., & Haig, B. (2020). Theory construction methodology: A practical framework for theory formation in psychology. PsyArXiv. doi: https://doi.org/10.31234/osf.io/w5tp8
Buhrmester, V., Müch, D., & Arens, M. (2019). Analysis of explainers of black box deep neural networks for computer vision: A survey. arXiv. Retrieved from https://arxiv.org/abs/1911.12116
Burger, J., Isvoranu, A.-M., Lunansky, G., Haslbeck, J., Epskamp, S., Hoekstra, R., … Blanken, T. (2020). Reporting standards for psychological network analyses in cross-sectional data. PsyArXiv. doi: https://doi.org/10.31234/osf.io/4y9nz
Chen, J., & Chen, Z. (2008). Extended bayesian information criteria for model selection with large model spaces. Biometrika, 95, 759–771. doi: https://doi.org/10.1093/biomet/asn034
Chicco, D., & Jurman, G. (2020). The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genomics, 21, 6. doi: https://doi.org/10.1186/s12864-019-6413-7
Christensen, A. P., Garrido, L. E., & Golino, H. (2021). Comparing community detection algorithms in psychological data: A Monte Carlo simulation. PsyArXiv. doi: https://doi.org/10.31234/osf.io/hz89e
Christensen, A. P., & Golino, H. (2019). Estimating the stability of the number of factors via Bootstrap Exploratory Graph Analysis: A tutorial. PsyArXiv. doi: https://doi.org/10.31234/osf.io/9deay
Christensen, A. P., & Golino, H. (2021). On the equivalency of factor and network loadings. Behavior Research Methods. doi: https://doi.org/10.3758/s13428-020-01500-6
Christensen, A. P., Golino, H., & Silvia, P. J. (2020). A psychometric network perspective on the validity and validation of personality trait questionnaires. European Journal of Personality, 34, 1095–1108. doi: https://doi.org/10.1002/per.2265
Cohen, J. (1992). A power primer. Psychological Bulletin, 112, 155–159. doi: https://doi.org/10.1037/0033-2909.112.1.155
Comrey, A. L., & Lee, H. B. (2013). A first course in factor analysis (2nd ed.). New York, NY: Psychology Press.
Cramer, A. O. J., van der Sluis, S., Noordhof, A., Wichers, M., Geschwind, N., Aggen, S. H., … Borsboom, D. (2012). Dimensions of normal personality as networks in search of equilibrium: You can’t like parties if you don’t like people. European Journal of Personality, 26, 414–431. doi: https://doi.org/10.1002/per.1866
Cramer, A. O. J., Waldrop, L. J., van der Maas, H. L., & Borsboom, D. (2010). Comorbidity: A network perspective. Behavioral and Brain Sciences, 33, 137–150. doi: https://doi.org/10.1017/S0140525X09991567
Csardi, G., & Nepusz, T. (2006). The igraph software package for complex network research. InterJournal, Complex Systems, 1695, 1–9. Retrieved from https://www.semanticscholar.org/paper/The-igraph-software-package-for-complex-network-Cs/\%C3/\%A1rdi-Nepusz/1d2744b83519657f5f2610698a8ddd177ced4f5c?p2df
DeVellis, R. F. (2017). Scale development: Theory and applications (4th ed.). Thousand Oaks, CA: SAGE Publications.
Donnellan, M. B., Oswald, F. L., Baird, B. M., & Lucas, R. E. (2006). The mini-IPIP scales: Tiny-yet-effective measures of the Big Five factors of personality. Psychological Assessment, 18, 192–203. doi: https://doi.org/10.1037/1040-3590.18.2.192
Dozat, T. (2016). Incorporating Nesterov momentum in Adam. In Proceedings of 4th international conference on learning representations, workshop track (pp. 604–612). San Juan, Puerto Rico. Retrieved from https://openreview.net/forum?id=OM0jvwB8jIp57ZJjtNEZ
Dreiseitl, S., & Ohno-Machado, L. (2002). Logistic regression and artificial neural network classification models: A methodology review. Journal of Biomedical Informatics, 35, 352–359. doi: https://doi.org/10.1016/S1532-0464(03)00034-0
Edwards, J. R., & Bagozzi, R. P. (2000). On the nature and direction of relationships between constructs and measures. Psychological Methods, 5, 155–174. doi: https://doi.org/10.1037/1082-989X.5.2.155
Epskamp, S., & Fried, E. I. (2018). A tutorial on regularized partial correlation networks. Psychological Methods, 23, 617–634. doi: https://doi.org/10.1037/met0000167
Epskamp, S., Rhemtulla, M., & Borsboom, D. (2017). Generalized network psychometrics: Combining network and latent variable models. Psychometrika, 82, 904–927. doi: https://doi.org/10.1007/s11336-017-9557-x
Fisher, A., Rudin, C., & Dominici, F. (2019). All models are wrong, but many are useful: Learning a variable’s importance by studying an entire class of prediction models simultaneously. Journal of Machine Learning Research, 20, 1–81. Retrieved from https://jmlr.org/papers/v20/18-760.html
Fortunato, S. (2010). Community detection in graphs. Physics Reports, 486, 75–174. doi: https://doi.org/10.1016/j.physrep.2009.11.002
Fried, E. I. (2020). Lack of theory building and testing impedes progress in the factor and network literature. PsyArXiv. doi: https://doi.org/10.31234/osf.io/zg84s
Friedman, J., Hastie, T., & Tibshirani, R. (2008). Sparse inverse covariance estimation with the graphical lasso. Biostatistics, 9, 432–441. doi: https://doi.org/10.1093/biostatistics/kxm045
Friedman, J., Hastie, T., & Tibshirani, R. (2010). Regularized paths for generalized linear models via coordinate descent. Journal of Statistical Software, 22, 1–34. doi: https://doi.org/10.18637/jss.v033.i01
Friedman, J., Hastie, T., & Tibshirani, R. (2014). glasso: Graphical lasso – estimation of Gaussian graphical models. Retrieved from https://CRAN.R-project.org/package=glasso
Goldberg, L. R. (1999). A broad-bandwidth, public domain, personality inventory measuring the lower-level facets of several five-factor models. In I. Mervielde, I. Deary, F. De Fruyt, & F. Ostendorf (Eds.), Personality psychology in Europe (Vol. 7, pp. 7–28). Tilburg, The Netherlands: Tilburg University Press.
Golino, H., Christensen, A. P., Moulder, R., Kim, S., & Boker, S. M. (2020). Modeling latent topics in social media using Dynamic Exploratory Graph Analysis: The case of the right-wing and left-wing trolls in the 2016 US elections. PsyArXiv. doi: https://doi.org/10.31234/osf.io/tfs7c
Golino, H., & Epskamp, S. (2017). Exploratory Graph Analysis: A new approach for estimating the number of dimensions in psychological research. PLoS ONE, 12, e0174035. doi: https://doi.org/10.1371/journal.pone.0174035
Golino, H., Shi, D., Christensen, A. P., Garrido, L. E., Nieto, M. D., Sadana, R., … Martinez-Molina, A. (2020). Investigating the performance of Exploratory Graph Analysis and traditional techniques to identify the number of latent factors: A simulation and tutorial. Psychological Methods, 25, 292–320. doi: https://doi.org/10.1037/met0000255
Gordon, E. M., Laumann, T. O., Marek, S., Raut, R. V., Gratton, C., Newbold, D. J., … others. (2020). Default-mode network streams for coupling to language and control systems. Proceedings of the National Academy of Sciences, 117, 17308–17319. doi: https://doi.org/10.1073/pnas.2005238117
Guyon, H., Falissard, B., & Kop, J.-L. (2017). Modeling psychological attributes in psychology–an epistemological discussion: Network analysis vs. latent variables. Frontiers in Psychology, 8, 798. doi: https://doi.org/10.3389/fpsyg.2017.00798
Hallquist, M., Wright, A. C. G., & Molenaar, P. C. M. (2019). Problems with centrality measures in psychopathology symptom networks: Why network psychometrics cannot escape psychometric theory. Multivariate Behavioral Research. doi: https://doi.org/10.1080/00273171.2019.1640103
Haslbeck, J., Ryan, O., Robinaugh, D., Waldorp, L., & Borsboom, D. (2019). Modeling psychopathology: From data models to formal theories. PsyArXiv. doi: https://doi.org/10.31234/osf.io/jgm7f
He, K., Zhang, X., Ren, S., & Sun, J. (2015). Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE international conference on computer vision (pp. 1026–1034).
Heaton, J. (2008). Introduction to neural networks with Java (2nd ed.). St. Louis, MO: Heaton Research, Inc.
Hornik, K. (1991). Approximation capabilities of multilayer feedforward networks. Neural Networks, 4, 251–257. doi: https://doi.org/10.1016/0893-6080(91)90009-T
Hurley, R. S., Losh, M., Parlier, M., Reznick, J. S., & Piven, J. (2007). The broad autism phenotype questionnaire. Journal of Autism and Developmental Disorders, 37(9), 1679–1690.
Ingersoll, B., Hopwood, C. J., Wainer, A., & Donnellan, M. B. (2011). A comparison of three self-report measures of the broader autism phenotype in a non-clinical sample. Journal of Autism and Developmental Disorders, 41, 1646–1657. doi: https://doi.org/10.1007/s10803-011-1192-2
James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An introduction to statistical learning. New York, NY: Springer. doi: https://doi.org/10.1007/978-1-4614-7138-7
Jessen, L. E. (2021). nnvizRt: A server for visualizing architectures of neural networks. Retrieved from https://leonjessen.shinyapps.io/nnvizRt/
John, O. P., Donahue, E. M., & Kentle, R. L. (1991). The Big Five Inventory—Versions 4a and 54. Berkeley, CA: University of California, Berkeley, Institute of Personality and Social Research.
Karpathy, A. (2019). A recipe for training neural networks. Retrieved April 25, 2019, from https://karpathy.github.io/2019/04/25/recipe/
Kingma, D. P., & Ba, J. (2014). Adam: A method for stochastic optimization. arXiv. Retrieved from https://arxiv.org/abs/1412.6980
Kruis, J., & Maris, G. (2016). Three representations of the Ising model. Scientific Reports, 6, srep34175. doi: https://doi.org/10.1038/srep34175
Lauritzen, S. L. (1996). Graphical models. Oxford, UK: Clarendon Press.
Marsman, M., Borsboom, D., Kruis, J., Epskamp, S., van Bork, R., Waldorp, L. J., … Maris, G. (2018). An introduction to network psychometrics: Relating Ising network models to item response theory models. Multivariate Behavioral Research, 53, 15–35. doi: https://doi.org/10.1080/00273171.2017.1379379
McNeish, D., & Wolf, M. G. (2020). Thinking twice about sum scores. Behavior Research Methods. doi: https://doi.org/10.3758/s13428-020-01398-0
Mohammadi, R., & Wit, E. C. (2015). BDgraph: An R package for Bayesian structure learning in graphical models. Journal of Statistical Software, 1–30. doi: https://doi.org/10.18637/jss.v089.i03
Mõtus, R., & Allerhand, M. (2017). Why do traits come together? The underlying trait and network approaches. In V. Ziegler-Hill & T. K. Shackelford (Eds.), SAGE handbook of personality and individual differences: The science of personality and individual differences (pp. 1–22). London, UK: SAGE Publications.
Muldoon, S. F., Bridgeford, E. W., & Bassett, D. S. (2016). Small-world propensity and weighted brain networks. Scientific Reports, 6, 22057. doi: https://doi.org/10.1038/srep22057
Nair, V., & Hinton, G. E. (2010). Rectified linear units improve restricted boltzmann machines. In International conference on machine learning (pp. 807–814). Haifa, Israel. Retrieved from https://icml.cc/Conferences/2010/papers/432.pdf
Newman, M. E. J. (2006). Modularity and community structure in networks. Proceedings of the National Academy of Sciences, 103, 8577–8582. doi: https://doi.org/10.1073/pnas.0601602103
Newman, M. E. J. (2010). Networks: An introduction. New York, NY: Oxford University Press. doi: https://doi.org/10.1093/acprof:oso/9780199206650.001.0001
Nwankpa, C., Ijomah, W., Gachagan, A., & Marshall, S. (2018). Activation functions: Comparison of trends in practice and research for deep learning. arXiv. https://arxiv.org/abs/1811.03378
Pons, P., & Latapy, M. (2006). Computing communities in large networks using random walks. Journal of Graph Algorithms and Applications, 10, 191–218. doi: https://doi.org/10.7155/jgaa.00185
Prechelt, L. (2012). Early stopping – but when? In G. Montavon, G. B. Orr, & K.-R. Müller (Eds.), Neural networks: Tricks of the trade (2nd ed., pp. 53–68). Berlin, Germany: Springer-Verlan.
R Core Team. (2020). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. Retrieved from https://www.R-project.org/
Revelle, W. (2017). psych: Procedures for psychological, psychometric, and personality research. Evanston, Illinois: Northwestern University. Retrieved from https://CRAN.R-project.org/package=psych
Ruder, S. (2016). An overview of gradient descent optimization algorithms. arXiv. Retrieved from https://arxiv.org/abs/1609.04747
Shen, X., Tokoglu, F., Papademetris, X., & Constable, R. T. (2013). Groupwise whole-brain parcellation from resting-state fMRI data for network node identification. NeuroImage, 82, 403–415. doi: https://doi.org/10.1016/j.neuroimage.2013.05.081
Sontag, E. D. (1991). Feedback stabilization using two-hidden-layer nets. In 1991 American control conference (pp. 815–820). Boston, MA: IEEE. doi: https://doi.org/10.23919/ACC.1991.4791486
Sutskever, I., Martens, J., Dahl, G., & Hinton, G. (2013). On the importance of initialization and momentum in deep learning. In International conference on machine learning (pp. 1139–1147). Atlanta, GA. Retrieved from https://www.jmlr.org/proceedings/papers/v28/sutskever13.pdf
Telesford, Q. K., Joyce, K. E., Hayasaka, S., Burdette, J. H., & Laurienti, P. J. (2011). The ubiquity of small-world networks. Brain Connectivity, 1(5), 367–375. doi: https://doi.org/10.1089/brain.2011.0038
Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological), 267–288. doi: https://doi.org/10.1111/j.2517-6161.1996.tb02080.x
van Bork, R., Rhemtulla, M., Waldorp, L. J., Kruis, J., Rezvanifar, S., & Borsboom, D. (2019). Latent variable models and networks: Statistical equivalence and testability. Multivariate Behavioral Research, 1–24. doi: https://doi.org/10.1080/00273171.2019.1672515
van der Maas, H. L. J., Dolan, C. V., Grasman, R. P. P. P., Wicherts, J. M., Huizenga, H. M., & Raijmakers, M. E. J. (2006). A dynamical model of general intelligence: The positive manifold of intelligence by mutualism. Psychological Review, 113, 842–861. doi: https://doi.org/10.1037/0033-295X.113.4.842
Waldorp, L., & Marsman, M. (2020). Relations between networks, regression, partial correlation, and latent variable model. arXiv. Retrieved from https://arxiv.org/abs/2007.10656
Ward, J. H. (1963). Hierarchical clustering to optimise an objective function. Journal of the American Statistical Association, 58, 238–244.
Watt, J., Borhani, R., & Katsaggelos, A. (2016). Machine learning refined: Foundations, algorithms, and applications. Cambridge, UK: Cambridge University Press. doi: https://doi.org/10.1017/CBO9781316402276
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature, 393, 440–442. doi: https://doi.org/10.1038/30918
Williams, D. R., Rhemtulla, M., Wysocki, A. C., & Rast, P. (2019). On nonregularized estimation of psychological networks. Multivariate Behavioral Research, 54, 719–750. doi: https://doi.org/10.1080/00273171.2019.1575716
Wright, A. G., & Woods, W. C. (2020). Personalized models of psychopathology. Annual Review of Clinical Psychology, 16. doi: https://doi.org/10.1146/annurev-clinpsy-102419-125032
Wysocki, A. C., & Rhemtulla, M. (2019). On penalty parameter selection for estimating network models. Multivariate Behavioral Research, 1–15. doi: https://doi.org/10.1080/00273171.2019.1672516
Yarkoni, T., & Westfall, J. (2017). Choosing prediction over explanation in psychology: Lessons from machine learning. Perspectives on Psychological Science, 12, 1100–1122. doi: https://doi.org/10.1177/1745691617693393
Zhou, Z.-H., Wu, J., & Tang, W. (2002). Ensembling neural networks: Many could be better than all. Artificial Intelligence, 137, 239–263. doi: https://doi.org/10.1016/S0004-3702(02)00190-X
Exploratory graph analysis (EGA; Golino & Epskamp, 2017; Golino et al., 2020) is a network psychometrics dimension identification method. The approach begins by estimating a network from the empirical data and applying a community detection algorithm to identify communities (or dimensions) in the network. The traditional EGA method estimates a Gaussian graphical model (GGM; Lauritzen, 1996) where nodes are variables and edges are the partial correlations between nodes after being conditioned on all other nodes. In psychological networks, the most common way of estimating a GGM is to use the graphical least absolute shrinkage and selection operator (GLASSO; Friedman, Hastie, & Tibshirani, 2008; Friedman, Hastie, & Tibshirani, 2014) with extended Bayesian information criterion (EBICglasso; Chen & Chen, 2008; Epskamp & Fried, 2018). Once the EBICglasso is applied, the Walktrap (Pons & Latapy, 2006) community detection algorithm is applied. The Walktrap algorithm uses random walks or stochastic steps from one node over an edge to another to determine the distance and similarity between two nodes. These random walks tend to stay within subsets of related nodes because they tend to be closer and more similar to one another. The algorithm merges the results, based on an agglomerative clustering approach (Ward, 1963), of the random walks to separate the communities. Modularity or the extent to which nodes maximize the proportion of connections within their community relative to connections to other communities (Newman, 2006) is then used as criterion for selecting the optimal clustering (or community) organization.
Following the same data generating procedures in the main text, we generated 480,000 datasets in total. For the factor models, we manipulated number of variables per factor (3, 4, 5, 6, and 7), number of factors (3, 4, 5, and 6), and correlations between factors (.00, .30, .50, and .70). In total, there were 240 conditions (sample size \(\times \) number of variables per factor \(\times \) number of factors \(\times \) correlations between factors). For each condition, 1,000 samples were generated.
In contrast to previous simulation studies on psychological networks which have generated data from random network models (e.g., Epskamp, Rhemtulla, & Borsboom, 2017; van Bork et al., 2019; Williams, Rhemtulla, Wysocki, & Rast, 2019), we generated the training network models based on small-world networks. Despite being the most widely studied type of network, random network models are largely incongruous with most real-world networks (e.g., lack of clustering, no correlation between degrees of adjacent nodes, shape of degree distribution; Newman, 2010). Small-world networks, however, at least mirror some properties of real-world networks (e.g., clustering, shortcuts between nodes; Newman, 2010) and are commonly found in real-world networks (e.g., brain networks; Muldoon, Bridgeford, & Bassett, 2016). Therefore, small-world networks are more likely to represent many psychological phenomena (e.g., psychopathology; Borsboom, Cramer, Schmittmann, Epskamp, & Waldorp, 2011). Moreover, the structure of small-world networks (high clustering and low distances between nodes) is closer to structures produced by factor models than random networks. We manipulated number of variables (10, 20, 30, and 40), density (.20, .40, .60, and .80), and rewiring probability (.01, .05, .10, .25, and .50). In total, there were 240 conditions (sample size \(\times \) number of variables \(\times \) neighborhood \(\times \) rewiring probability). For each condition, we generated 1,000 samples.
Formal articles on steps for how to train neural networks appropriately are sparse; however, there are several resources available. Our approach followed Andrej Karpathy’s “recipe” for training neural networks (Karpathy, 2019). This recipe starts by thoroughly inspecting the data distributions and looking for patterns, developing a neural network skeleton by making a simplified model, overfitting a small portion of samples (e.g., 100) from the data, regularizing the model to prevent overfitting (e.g., early stopping), optimizing hyperparameters (e.g., number of nodes and hidden layers, learning rate, batch size), and using neural network ensembles (which we describe in our Introduction section). To prevent overfitting of the training data, we added an early stopping criterion: when the validation loss plateaued (i.e., decreases in the loss function less than .001) for ten epochs (or ten runs through the entire training dataset; Prechelt, 2012), then the best weights (highest training accuracy) were kept and used as our model.
Neural networks require a specific structure for input. We used the proportion of loading effect sizes to summarize the covariance matrix into a specific set of variables for input. This approach makes it so that no matter how many variables are in a dataset they can always be summarized into the same variables that are fed into the neural network. Using proportions that are equal to or larger than a certain effect size allows for more continuous cut-offs that reduce some of arbitrariness that is inherent in rule-of-thumb effect sizes.
Following Christensen and Golino’s (2021) LCT algorithm, we submitted each dataset to EGA and EFA (using the same number of dimensions estimated by EGA). For both the network and factor loadings, we computed the proportion of loadings that were greater than small (.15 and .40, respectively), moderate (.25 and .55, respectively), and large (.35 and .70, respectively) effect sizes as well as the proportion of loadings that were greater than small effect sizes for dominant and cross-loadings (Christensen & Golino, 2021; Comrey & Lee, 2013). For each dataset, this created 10 proportions in total (five proportions for each loading type) that were used as the base input nodes for all neural networks.
Additional input nodes were created by computing the ratio between the exponent of a base network loading (i.e., small, moderate, large, dominant, and cross) and the exponent of the corresponding base factor loading. To normalize these ratios to be between zero and one (the same range as the proportions), we used min-max normalization using the minimum and maximum possible ratio:
\[\frac {x - \frac {\exp (0)}{\exp (1)}}{\frac {\exp (1)}{\exp (0)} - \frac {\exp (0)}{\exp (1)}},\] where \(x\) is the ratio between the exponent of a network loading proportion (e.g., small) and the exponent of the corresponding factor loading proportion. Additional inputs were not included if they did not increase prediction beyond the base model when training the logistic regression. For all models, only the dominant ratio improved the accuracy of the logistic regression predictions. When additional inputs were used, we mention them in their corresponding neural network descriptions. Below is a figure representing the data processing pipeline to be fed data into the neural network (Figure 4).
Figure 4 displays simulated data from a factor model with two factors, six variables per factor, small correlations between factors (0.30), and sample size of 1000. The pipeline from data to neural network starts by computing a correlation matrix. Next, EGA is used to estimate the number of dimensions. These dimensions are then used as the number of factors to estimate in an EFA model with oblimin rotation. Factor and network loadings are then computed. The proportion of loadings that are greater than or equal to small, moderate, and large effect sizes are computed. Similarly, the proportion of dominant and cross-loadings that are greater than or equal to a small effect size are computed. This is done for both factor and network loadings. Finally, these loadings are fed as input into the neural network. The neural network then predicts the model that the data were generated from. The neural network was visualized using the nnvizRt Shiny application (Jessen, 2021) in R.
Activation functions determine the output from a node given the input to the node. All hidden layers for all neural networks used the Parametric Rectified Linear Unit (PReLu; He, Zhang, Ren, & Sun, 2015) activation function. The Rectified Linear Unit (ReLu; Nair & Hinton, 2010) is the contemporary choice for most applications of deep learning (as opposed to the historically and often still used sigmoid function; Nwankpa, Ijomah, Gachagan, & Marshall, 2018). The ReLu activation function is a non-linear function that returns the input of the function as the output unless the input is negative, which is instead set to zero (inspired by the action potential of biological neurons). One limitation of the ReLu function is that it can cause some neurons to never activate (no matter the input), always outputting zero (known as the “dying neuron problem”; He, Zhang, Ren, & Sun, 2015). PReLu overcomes this issue by allowing a trainable parameter \(\alpha \) to be adjusted so that some small non-zero negative weights still activate neurons in the network. When \(\alpha \) is zero for a node, then PReLu is equivalent to ReLu. This flexibility of PReLu allows it to perform at least as well as ReLu. For all output layers, we used the sigmoid function (\(\frac {e^x}{e^x + 1}\)) to estimate the probability of a given sample belonging to the outcome model (i.e., the model designated as 1 in the output). A cut-off probability of .50 was used to determine what model the sample belonged to (e.g., factor vs. network model).
For all models, we used the Nestorov Adaptive Moment Estimation optimizer (NADAM; Dozat, 2016), which tends to be the contemporary choice of neural networks (Ruder, 2016). The details of gradient descent optimizers are beyond the scope of this paper; however, their purpose was to minimize their functions by iteratively moving towards the steepest part of the gradient or slope of the loss function (Watt, Borhani, & Katsaggelos, 2016). At each iteration, the algorithm takes certain sized steps on the gradient, which are called the learning rate. Higher learning rates lead to larger steps toward a loss minimum but can potentially over-step a more optimal minimum; lower learning rates are more likely to reach an optimal minimum but take more time to get there. NADAM is an adaptive algorithm that changes the learning rate over time in order to achieve appropriate descent. The foundation of this algorithm is based on the Adaptive Moment Estimation (ADAM) optimizer (Kingma & Ba, 2014), but uses an alternative momentum parameter called Nesterov’s accelerated gradient momentum (NAG; Sutskever, Martens, Dahl, & Hinton, 2013). In NADAM, NAG moves toward an intermediate direction and then corrects toward the gradient, which allows the momentum to be shifted toward the minimum (even after moving past the minimum; for more details, see Dozat, 2016).
Gradient descent optimizers aim to minimize a loss function or the error between the actual and predicted outcomes. In our neural networks, this was binary cross entropy or logarithmic loss. Binary cross entropy is defined as the distance between two probability distributions (e.g., actual and predicted outcomes) and mathematically represented as:
\[CE = -\big (y \log (p) + (1 - y) \log (1 - p)\big ),\] where \(y\) is the actual model and \(p\) is the predicted probability of the dataset belonging to the model. If \(y = 1\), then \(CE\); otherwise, if \(y = 0\), then \(1 - CE\).
Binary accuracy was our accuracy measure, which is the mean of correct identifications in the total sample. The accuracy typically corresponds to loss but not necessarily. This is because correct model identifications are part of the binary cross entropy equation. Their difference arises in the fact that binary cross entropy considers the probability in which a dataset belongs to the correct model. In the random vs. non-random model, for example, a probability \(\ge .50\) would be considered a random model (1); otherwise, it is considered a non-random model (0). A correct identification would be a 1 but its probability could be as low as .50. In terms of binary cross entropy, the loss for a correct identification could range from 0 (\(p = 1\)) to 0.693 (\(p = .50\)). Therefore, loss is informative about the decisiveness of the predictions and accuracy is informative about the correctness of the predictions.
Models were set up with a certain number of samples, which were then split into the original training (80% of the overall sample) and validation (20% of the overall sample) samples. The original validation samples are then completely held out of the model training phase and were only seen after the model had been trained. The original training samples were used to train the model. During training, the original training samples are further split into a new training dataset (80% of the training samples) and validation dataset (20% of the training samples). This new training dataset is then randomly sampled without replacement with a specific number of batch sizes (number of training samples used in each update of the gradient and weights). After all of the new training dataset samples have been used once, the model is tested using the new validation dataset.
Loss and accuracy metrics are then provided with the training loss and accuracy representing the last model in the epoch and the validation loss and accuracy representing the performance of this last model on the validation dataset. The conclusion of a single run of this process is called an epoch. Each new epoch will randomly draw samples without replacement from the original training samples and form new training and validation datasets (a process known as shuffling). For all neural networks, we set the total number of epochs to 100 to allow training to proceed as necessary to settle into a minimum. Training was terminated when either the epochs reached 100 or our early stopping criterion was reached (i.e., decrease in validation loss less than .001 for ten consecutive epochs). After training was terminated, the final model was then tested on the original validation samples, which are considered to be novel because they had not been seen during the training of the model.
As a baseline comparison model, we trained the lasso regularized logistic regression models on the same original training data using the same input variables used in the neural networks. Regularized logistic regression models were chosen as a comparison for two reasons: (1) logistic regression models tend to perform better than other machine learning classification methods, such as support vector machines and decision trees, when there are overlapping classes, and (2) regularization reduces the flexibility of the model, which makes it less likely to overfit the underlying function in the training data and more likely to generalize to other data conditions (James, Witten, Hastie, & Tibshirani, 2013). The use of logistic regression models provides inference into whether more complex neural networks are necessary. The coefficients of each trained logistic model were extracted and then solved for each case of the original validation dataset. Accuracy and loss were then computed for the original validation dataset.
In order to determine the importance of each input into each neural network, we computed a measure of feature importance on the original validation datasets that were held out of the original training datasets following Fisher, Rudin, and Dominici (2019). The approach works by permutating one-by-one each input variable and computing the loss. The loss is then divided by the original loss to obtain the relative decrease in performance for the permutated input. Because of the stochasticity of the permutations, we computed this analysis ten times and computed the mean of the values. Values greater than one suggest the input was important with larger values suggesting greater importance whereas values near one suggest that the input did not improve the model and less than one suggest that the input made the model worse.
All analyses were performed in R. All neural networks were trained using the keras package (Allaire & Chollet, 2020) and all logistic regression models were fit with the glmnet package (Friedman, Hastie, & Tibshirani, 2010). All data, R code and scripts are available on the Open Science Framework (OSF). Each neural network is available on the OSF and can be further fine-tuned and improved with new data and examples (i.e., the models can be further trained with new models, data conditions, and methods of data generation).
The mean proportions of the base network and factor loadings across each data-generating models are presented in Figure 5.
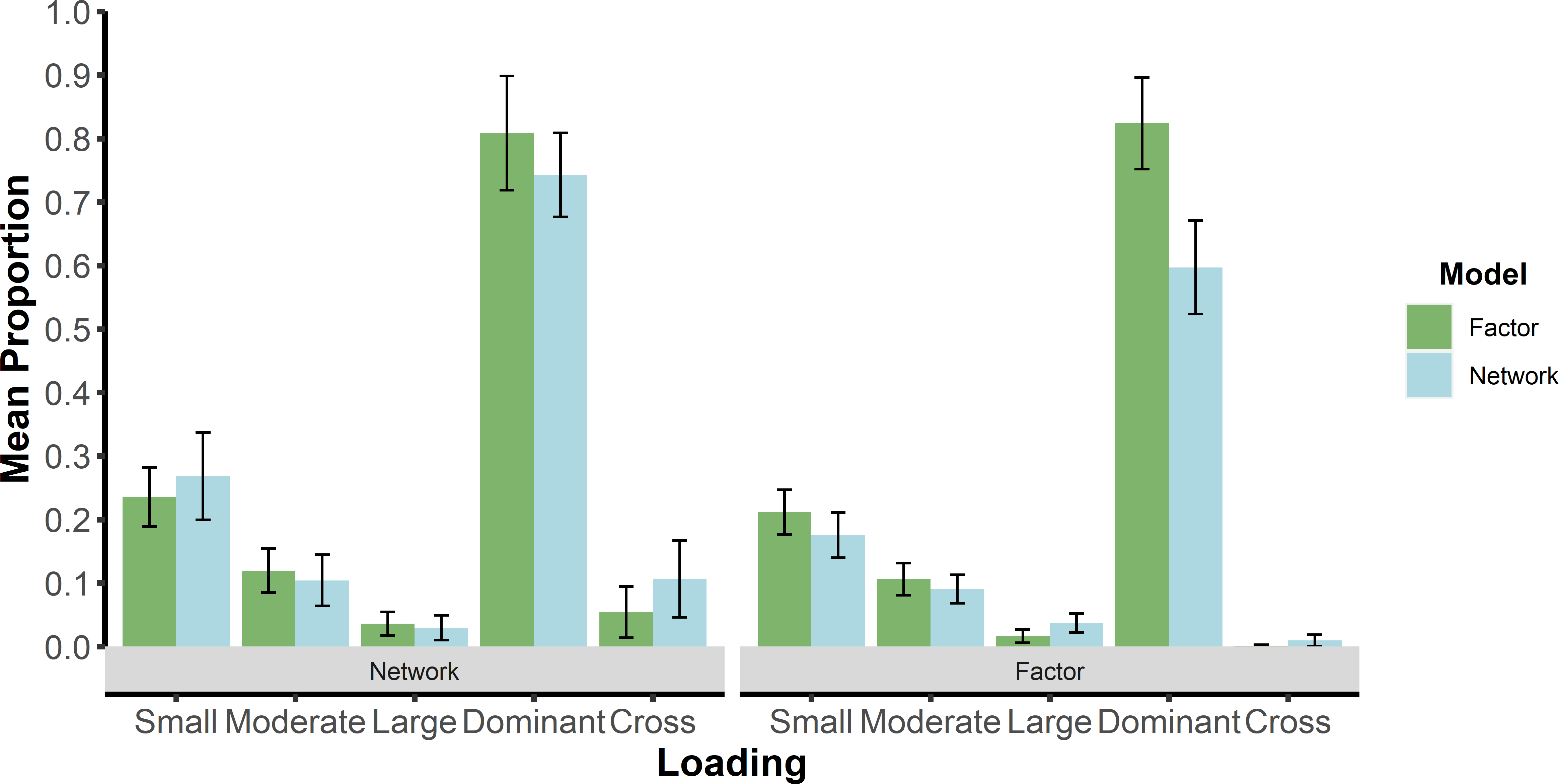
The most glaring differences between models are proportion of dominant loadings that achieve a small effect size or larger for both network and factor loadings. This difference is most apparent when the data are generated from a network model. Table 1 presents a summary of the architecture the neural networks including the parameters and validation estimates.
Across all neural networks, we found comparable or better performance than the logistic regression models, suggesting that the neural networks were reasonable and potentially necessary for optimal performance in the LCT algorithm.
Model 1: Low Correlation Factor vs. Network. For the low correlation factor vs. network model, we removed the datasets corresponding to the data generated from factor models with correlations between factors of .50 and .70 (120,000 samples), leaving us with 120,000 samples of orthogonal and low correlations between factors (.00 and .30, respectively). To obtain an equivalent number of datasets generated from the network models, we randomly sampled 40,000 network datasets from each level of sample size (i.e., 250, 500, and 1000), resulting in 120,000 total network datasets. In total, we used 240,000 datasets.
We created a single binary output variable with 1 corresponding to a factor model and 0 corresponding to not a low correlation factor model. Importantly, it is possible that the learned weights of the low correlation factor model could still correspond to other factor models even though they weren’t observed in the trained model. This potential for overlap was on purpose and allowed multiple checks of factor models to be learned against network models in the LCT algorithm.
The input of this model consisted of our base input nodes along with an additional input: dominant ratio. This made for eleven input nodes in total. There was one hidden layer with nine nodes. Our final model did not reach our early stopping criterion and was terminated after the \(100^{\text {th}}\) epoch. We then evaluated the model on the validation dataset, which achieved a loss of 0.180 and accuracy of 92.8%. The neural network model outperformed the regularized logistic regression model by a full tenth in loss and over three percent in accuracy (Table 1). The inputs that had the greatest importance were the cross factor loading (2.57), dominant factor loading (2.55), and large factor loading (2.12).
Model 2: High Correlation with Variables per Factor Greater than Factors vs. Network. The setup of the high correlation with variables greater than factors vs. network model was identical to Model 1 except the samples retained were the high correlation between factors (i.e., .50 and .70; 120,000 samples) rather than the low correlation between factors. From these samples, we extracted samples that were generated with the number of variables per factor that were greater than the number of factors (e.g., 4 variables per factor and 3 factors). This resulted in 60,000 samples used in training. Just as Model 1, we randomly sampled an equal number of network samples across the same sample size levels, resulting in a total of 120,000 samples.
The exact same input and hidden layers were used as Model 1. Similarly, our final model did not meet our early stopping criterion and was terminated after the \(100^{\text {th}}\) epoch. We then evaluated the model on the validation dataset, which achieved a loss of 0.159 and accuracy of 93.7%. This neural network outperformed the logistic regression model in loss and accuracy (Table 1). The inputs that had the greatest importance were the cross factor loading (3.28), small factor loading (3.07), and large factor loading (2.44).
Model 3: High Correlation with Variables per Factor Less than or Equal to Factors vs. Network. The setup of the high correlation with variables less than or equal to factors vs. network model was the same as Model 2 except models with the samples retained were the moderate and high correlation between factors (i.e., .50 and .70) with variables per factor than were equal to or less than the number of factors (60,000 samples; e.g., 3 variables per factor and 5 factors). Similarly, an equivalent number of network models were randomly drawn from the 240,000 network models (across the same sample size levels), resulting in a total of 120,000 samples. The inputs and hidden layers were the same as Model 1 and 2. Our final model reached our threshold of early stopping on epoch 88. We then evaluated the model on the validation dataset, which achieved a loss of 0.239 and accuracy of 90.2%. Relative to the other models, the neural network substantially outperformed the logistic regression model on both loss and accuracy (differences of .162 and 5.6%, respectively). The inputs that had the greatest importance were the small network loading (6.65), cross factor loading (2.45), and dominant factor loading (2.22).
To demonstrate how the structure of data can be manipulated toward a certain model, we used a dataset that consisted of 2,832 observations on items from the Broad Autism Phenotype Questionnaire (BAPQ; Hurley, Losh, Parlier, Reznick, & Piven, 2007) that was a collected as a part of the Simons Foundation Autism Research Initiative’s Simplex Collection (https://www.sfari.org/). The BAPQ was completed by the mothers and fathers of children on the Autism spectrum. The BAPQ consists of three sub-scales—aloof personality, pragmatic language problems, and rigid personality—that are based on direct assessment interviews with parents of autistic people that correspond to defining behavioral domains of autism: social, communication deficits, and stereotyped-repetitive behaviors (Hurley, Losh, Parlier, Reznick, & Piven, 2007). The BAPQ has demonstrated a robust three-factor structure (Ingersoll, Hopwood, Wainer, & Donnellan, 2011) with each sub-scale containing twelve items that are rated on a 6-point Likert scale. Correlations between the means of the sub-scales tend to be highly correlated in clinical samples (\(r\)’s from .50 to .70; Hurley, Losh, Parlier, Reznick, & Piven, 2007) but smaller when using factor analysis in non-clinical samples (\(r\)’s from .10 to .30; Ingersoll, Hopwood, Wainer, & Donnellan, 2011).
Because we have data for both mothers and fathers, we applied the LCT to each parent’s datasets. We split the datasets into training (n = 1,699) and testing (n = 1,133) sets to validate the LCT’s results. Below we present a table (Table 3) for the predictions of the LCT.
The results demonstrate that the BAPQ in mothers is a factor model based on the empirical prediction and network model based on the bootstrap and proportion prediction. For the fathers, the training data were predicted to be a factor model across all predictions while the testing data were predicted to be a network model across all predictions. In short, the results are mixed but lean towards a network model with three out of for datasets having network predictions for the proportion prediction. Based on this result, we would conclude that the data for mothers and fathers are most likely generated from a network model. Notably, the fathers’ datasets were leaning towards a factor model relative to the mothers datasets (including the training data being a factor model across predictions).
If, for example, we thought that the data generating mechanism was a factor model, then we should try to adjust the data’s structure toward a factor model. To do so, we could analyze the structure of the data to see which items are multidimensional or leading to larger cross-loadings between dimensions. One approach for achieving these results is called bootstrap exploratory graph analysis (bootEGA; Christensen & Golino, 2019).
bootEGA applies a parametric bootstrap approach where N number of replicate samples are generated from a multivariate normal distribution based on the empirical correlation matrix. Each replicate sample is then analyzed using EGA (see Appendix A.1 for a description), forming a distribution of factors and item placement within those factors. Taking advantage of the deterministic allocation of items into factors, we can determine how often items are replicating in their empirical dimension as well as other dimensions. That is, we can determine how stable the factors are with respect to how items are placed into them (Christensen, Golino, & Silvia, 2020). Items that are not replicating well in their empirically derived factor (e.g., EGA identified factor) indicate that these items are likely to be multidimensional, have larger cross-loadings, and are likely leading the data structure to be more like a network model.
When performing such an analysis, we found that there were four factors with identical item placement for the mothers and fathers datasets’ empirically derived structure (using EGA). Using this factor structure and item placement, we applied bootEGA (n = 500) to the training and testing datasets for both mothers and fathers. The item stability analysis found one factor containing items that were relative unstable. These items and their stability (number of times replicating in their empirically derived structure) are presented in Table 4. When removing these items, the data structure for all datasets moved closer to a factor model structure as shown in Table 5.
Indeed, three out of four datasets now suggest a factor model relative to a network model. For those three models suggesting a factor model (mothers training and both fathers), all predictions were for a factor model. The testing mothers dataset was a network across all predictions but notably the proportions prediction suggested that the model moved away from a network model and closer to a factor model (from 0.71 to 0.58 for a network model and 0.29 to 0.42 for a factor model).