Keywords: Bayesian Estimation ● Missing Data ● Latent Growth Curve Models ● Non-ignorable Missingness ● Longitudinal Analysis ● Multilevel Modeling
In social and behavioral sciences, there has been great interest in the analysis of change (e.g., Collins, 1991; Lu, Zhang, & Lubke, 2010; Singer & Willett, 2003). Growth modeling is designed to provide direct information of growth by measuring the variables of interest on the same participants repeatedly through time (e.g., Demidenko, 2004; Fitzmaurice, Davidian, Verbeke, & Molenberghs, 2008; Fitzmaurice, Laird, & Ware, 2004; Hedeker & Gibbons, 2006; Singer & Willett, 2003). Among the most popular growth models, latent growth curve models (LGCMs) are becoming increasingly important because they can effectively capture individuals’ latent growth trajectories and also explain the latent factors that influence such growth by analyzing the repeatedly measured manifest variables (e.g., Baltes & Nesselroade, 1979). Manifest variables are evident in the data, such as observed scores; latent variables cannot be measured directly and are essentially hidden in the data, such as the latent initial levels and latent growth rates (Singer & Willett, 2003). We use the term “latent” because these variables are not directly observable but rather are assumed to be inferred, although they may be closely related to observed scores. For example, the latent intercept (i.e., the latent initial level) may be related to the test score at the first occasion, the prior knowledge of a course (such as mathematical knowledge), or other similar variables. The latent slope (i.e., the latent growth rate) may be related to the participant’s learning ability, the attitude toward the course, the instructor’s teaching methods, or other similar types of variables.
However, with an increase in complexity of LGCMs, comes an increase in difficulties estimating such models. First, missing data are almost inevitable with longitudinal data (e.g., Jelicic, Phelps, & Lerner, 2009; Little & Rubin, 2002). Second, conventional likelihood estimation procedures might fail for complex models with complicated data structures.
As LGCMs involve data collection on the same participants through multiple waves of surveys, tests, or questionnaires, missing data are almost inevitable. Research participants may drop out of a study, or some students may miss a test due to absence or fatigue (e.g., Little & Rubin, 2002; Schafer, 1997). Missing data can be investigated from their mechanisms, or why missing data occur. Little and Rubin (2002) distinguished ignorable missingness mechanism and non-ignorable missingness mechanism. For ignorable missingness mechanism, estimates are usually asymptotically consistent when the missingness is ignored (Little & Rubin, 2002), because the parameters that govern the missing process either are distinct from the parameters that govern the model outcomes or depend on the observed variables in the model. The non-ignorable missingness mechanism is also referred to as missing not at random (MNAR), in which the missing data probability depends either on unobserved outcomes, or on latent variables that cannot be fully measured by the observed data, in other words, latent variables that depend on the missing values.
With the appearance of missing data comes the challenge in estimating growth model parameters. To address the challenge, statisticians have developed different approaches and models. Although there are a large amount of literature to address this problem in applied behavioral sciences (e.g., Acock, 2005; Schafer & Graham, 2002; Schlomer, Bauman, & Card, 2010), especially in longitudinal studies (e.g., Jelicic et al., 2009; Roth, 1994), the majority of the literature is on ignorable missingness. This is mainly because (1) analysis models or techniques for non-ignorable missing data are traditionally difficult to implement and not yet easy to use (e.g., Baraldi & Enders, 2010), and (2) missingness mechanisms are not testable (e.g., Little & Rubin, 2002). At the same time, however, non-ignorable missingness analysis is a crucial and a serious concern in applied research areas, in which participants may be dropping out for reasons directly related to the response being measured (e.g., Baraldi & Enders, 2010; Enders, 2011b; Hedeker & Gibbons, 1997). Not attending to the non-ignorable missingness may result in severely biased statistical estimates, standard errors, and associated confidence intervals, and thus poses substantial risk of leading researchers to incorrect conclusions (e.g., Little & Rubin, 2002; Schafer, 1997; Zhang & Wang, 2012).
In a study of latent growth models, Lu, Zhang, and Lubke (2011) investigated non-ignorable missingness in mixture models. However, the missingness in that study was only allowed to depend on latent class membership. In practice, even within one population, the missingness may depend on many other latent variables, such as latent initial levels and latent growth rates. When observed data are not completely informative about these latent variables, the missingness is non-ignorable. Furthermore, Lu et al. (2011) did not examine how to identify the missingness mechanisms. Accordingly, this study extends previous research to more general non-ignorable missingness and also investigates the influences of different types of non-ignorable missingness on model estimation.
To implement the model estimation, we propose a full Bayesian approach. Traditionally, maximum likelihood methods have been widely used in most studies for estimating parameters of models in the presence of missing data (e.g., Enders, 2011a; Muthén, Asparouhov, Hunter, & Leuchter, 2011), and statistical inferences have been carried out using conventional likelihood procedures (e.g., Yuan & Lu, 2008). Recently, multiple imputation (MI) methods have been proposed as an alternative approach (e.g., Enders, 2011a; Muthén et al., 2011). MI is a Monte Carlo technique that replaces the missing values with multiple simulated values to generate multiple complete datasets. Each of these simulated datasets is then analyzed using methods that do not account for missingness, that is, using standard analytical methods. Results are then combined to produce estimates and confidence intervals that incorporate the uncertainty due to the missing-data (Enders, 2011a; Rubin, 1987; Schafer, 1997). Both ML and MI estimation methods typically assume that missing data mechanisms are MCAR or MAR. Further, using conventional estimation procedures may fail or may provide biased estimates (Yuan & Zhang, 2012) when estimating model parameters in complex models with complicated data structures such as GMMs with missing data and outliers. In addition, MI requires data to be imputed under a particular model (e.g., Allison, 2002; Newman, 2003). And literature also shows that multiple imputation is inappropriate as a general purpose methodology for complex problems or large datasets (e.g., Fay, 1992). When missingness is MNAR, most work augments the basic analysis using with a model that explains the probability of missing data (e.g., Enders, 2011a; Muthén et al., 2011).
In this article, a full Bayesian estimate approach (e.g., Lee, 2007; Muthén & Asparouhov, 2012) is proposed. There are several advantages. First, this approach involves Gibbs sampling methods (Geman & Geman, 1984). Gibbs sampling is especially useful when the joint distribution is complex or unknown but the conditional distribution of each variable is available. The sequence of samples constructs a Markov chain that can be shown to be ergodic (Geman & Geman, 1984). That is, once convergence is obtained, the samples can be assumed to be independent draws from the stationary distribution. Thus, after convergence the generated value is actually from the joint distribution of all parameters. Each variable from the Markov chain has also been shown to converge to the marginal distribution of that variable (Robert & Casella, 2004). Additional advantages of Bayesian methods include their intuitive interpretations of statistical results, their flexibility in incorporating prior information about how data behave in similar contexts and findings from experimental research, their capacity for dealing with small sample sizes (such as occur with special populations), and their flexibility in the analysis of complex statistical models with complicated data structure (e.g., Dunson, 2000; Scheines, Hoijtink, & Boomsma, 1999).
The goals of the paper are to propose latent growth curve models with non-ignorable missingness and to evaluate the performance of Bayesian methods to recover model parameters. The rest of the article consists of four sections. Section 2 presents and formulates three non-ignorable missingness selection models. Section 3 presents a full Bayesian method to estimate the latent growth models through the data augmentation and Gibbs sampling algorithms. Section 4 conducts a simulation study. Estimates from models with different non-ignorable missingness and different sample sizes are summarized, analyzed, and compared. Conclusions based on the simulation study are drawn. Section 5 discusses the implications and future directions of this study. Finally, the appendix presents technical details.
In this section, we model the non-ignorable missingness in growth models. Before we introduce the three selection models, we first review the latent growth curve models (LGCMs).
The latent growth curve models (LGCMs) can be expressed by a regression equation with latent variables being regressors. Specifically, for a longitudinal study with $N$ subjects and $T$ measurement time points, let $\mathbf {y}_{i}=(y_{i1},y_{i2},...,y_{iT})'$ be a $T\times 1$ random vector, where $y_{it}$ stands for the outcome or observation of individual $i$ at occasion $t$ ($i=1,2,...,N$; $t=1,2,...,T$), and let $\boldsymbol {\eta }_{i}$ be a $q\times 1$ random vector containing $q$ continuous latent variables. A latent growth curve model for the outcome $\mathbf {y}_{i}$ related to the latent $\boldsymbol {\eta }_{i}$ can be written as
where $\mathbf {\Lambda }$ is a $T\times q$ matrix consisting of factor loadings, $\mathbf {e}_{i}$ is a $T\times 1$ vector of residuals or measurement errors that are assumed to follow multivariate normal distributions, i.e., $\mathbf {e}_{i} \sim MN_{T}(\textbf {0},\mathbf {\Theta })$ 1, and $\boldsymbol {\xi }_{i}$ is a $q\times 1$ vector that is assumed to follow a multivariate distribution, i.e., $\boldsymbol {\xi }_{i} \sim MN_{q}(\textbf {0},\mathbf {\Psi })$. In LGCMs, $\boldsymbol {\beta }$ is called fixed effects and $\boldsymbol {\xi }_{i}$ is called random effects (e.g., Fitzmaurice et al., 2004; Hedges, 1994; Luke, 2004; Singer & Willett, 2003). The vectors $\boldsymbol {\beta }$, $\boldsymbol {\eta }_{i}$, and the matrix $\mathbf {\Lambda }$ determine the growth trajectory of the model. For instance, when $q=2$, $\boldsymbol {\beta }=(I, S)'$, $\boldsymbol {\eta }_{i}=(I_{i}, S_{i})'$, and $\mathbf {\Lambda }$ is a $T\times 2$ matrix containing the first column of 1s and the second column of $(0, 1, ..., T-1)$. The corresponding model represents a linear growth model in which $I$ is the latent population intercept (or latent random initial level), $S$ is the latent population slope, $I_{i}$ is individual $i$’s latent random intercept and $S_{i}$ is individual $i$’s latent random slope. Furthermore, when $q=3$, $\boldsymbol {\beta }=(I, S, Q)'$, $\boldsymbol {\eta }_{i}=(I_{i}, S_{i}, Q_{i})'$, and $\mathbf {\Lambda }$ is a $T\times 3$ matrix containing the first column of 1s, the second column of $(0, 1, ..., T-1)$, and the third column of $(0, 1, ..., (T-1)^2)$. The corresponding model represents a quadratic growth curve model with $Q$ and $Q_{i}$ being latent quadratic coefficients for population and individual $i$, respectively.
To address the non-ignorable missingness, there are two general approaches, pattern-mixture models (Hedeker & Gibbons, 1997; Little & Rubin, 1987) and selection models (Glynn, Laird, & Rubin, 1986; Little, 1993, 1995). In both cases, the statistical analysis requires joint modelling of dependent variable and missing data processes. In this research, selection models are used, mainly for two reasons. First, substantively, it seems more natural to consider the behavior of the response variable in the full target population of interests, rather than in the sub-populations defined by missing data patterns (e.g., Fitzmaurice et al., 2008). Second, the selection model formulation leads directly to the joint distribution of both dependent variables and the missingness (e.g., Fitzmaurice et al., 2008) as follows,
|
|
where $f(.)$ is a density function, $\mathbf {x}_{i}$ is a vector of covariates for individual $i$, $\mathbf {y}_{i}$ is a vector of individual $i$’s outcome scores, $\mathbf {\Theta }=(\boldsymbol {\nu },\boldsymbol {\phi })$ are all parameters in the model, in which $\boldsymbol {\nu }$ are parameters for the growth model and $\boldsymbol {\phi }$ are parameters for the missingness, and $\mathbf {m}_{i}$ is a vector $\mathbf {m}_{i}=(m_{i1},m_{i2},...,m_{iT})'$ that indicates the missingness status for $\mathbf {y}_{i}$. Specifically, if $y_{i}$ is missing at time point $t$, then $m_{it}=1$; otherwise, $m_{it}=0$. Here, we assume the missingness is conditionally independent (e.g., Dawid, 1979), which means across different occasions the conditional distributions of missingness are independent with each other. Let $\tau _{it}=f(m_{it}=1)$ be the probability that $y_{it}$ is missing, then $m_{it}$ follows a Bernoulli distribution of $\tau _{it}$, and the density function of $m_{it}$ is $f(m_{it})=\tau _{it}^{m_{it}}(1-\tau _{it})^{1-m_{it}}$. For different non-ignorable missingness patterns, the expressions of $\tau _{it}$ are different. Lu et al. (2011) investigated the non-ignorable missingness in mixture models. The $\tau _{it}$ in that article is a function of latent class membership, and thus the missingness is Latent Class Dependent (LCD).
However, LCD was proposed in the framework of mixture models. Within each latent population, there is no class membership indicator. Consequently, the missingness is ignorable. In this article, we consider more complex non-ignorable missingness mechanisms within a population. In general, we assume $\mathbf {L}_{i}$ is a vector of latent variables that depend on the missing values. A general class of selection models for dealing with non-ignorable missing data in latent growth modelling can be formulated as
where $\mathbf {x}_i$ is an $r$-dimensional vector, $\boldsymbol {\omega }_{i}=(1, \mathbf {L}_{i}', \mathbf {x}_{i}')'$ and $\boldsymbol {\gamma }_{t}= (\gamma _{0t},\boldsymbol {\gamma }_{Lt}', \boldsymbol {\gamma }_{xt}')'$. The missingness is non-ignorable because it depends on the latent variables $\mathbf {L}_{i}$ in the model and the observed data are not completely informative about these latent variables. Note that the vector $\boldsymbol {\gamma }_{Lt}$ here should be non-zero. Otherwise, the missingness becomes ignorable.Specific sub-models under different situations can be derived from this general model. For example, missingness may be related to latent intercepts, latent growth rates, or potential outcomes. To show different types of non-ignorable missingness, we draw the path diagrams, as shown in Figures 1, 2, and 3, to illustrate the sub-models. These sub-models are based on three types of latent variables on which the missingness might depend. In these path diagrams, a square/rectangle indicates an observed variable, a circle/oval means a latent variable, a triangle represents a constant, and arrows show the relationship among them. $y_{t}$ is the outcome at time $t$, which is influenced by latent effects such as $I$, $S$, and $\eta _q$. As the value of $y_{t}$ might be missing, we use both circle and square in the path diagram. If $y_{t}$ is missing, then the potential outcome cannot be observed and the corresponding missingness indicator $m_{t}$ becomes 1. The dashed lines between $y_{t}$ and $m_{t}$ show the 1-1 relationship. In these sub-models, the value of $m_{t}$ depends on the observed covariate $x_{r}$ and some latent variables. The details of these three sub-models are described as follows.
It illustrates the situation where the missingness depends on individual’s latent intercept, $I_{i}$. For example, a student’s latent initial ability level of the knowledge of a course influences the likelihood of that participant dropping out of or staying in that course. If the latent initial ability of a course is not high, a student may choose to drop that course or even drop out a school. In the case of LID, the $\mathbf {L}_{i}$ in Equation (3) is simplified to a univariate $I_{i}$. Suppose that the missingness is also related to some observed covariates $\mathbf {x}_i$, such as parents’ education or family income, then $\tau _{Iit}$ is expressed as a probit link function of $I_{i}$ and $\mathbf {x}_i$
where $\boldsymbol {\omega }_{Ii}=(1, I_{i}, \mathbf {x}_{i}')'$ and $\boldsymbol {\gamma }_{It}= (\gamma _{0t},\gamma _{It}, \boldsymbol {\gamma }_{xt}')'$. 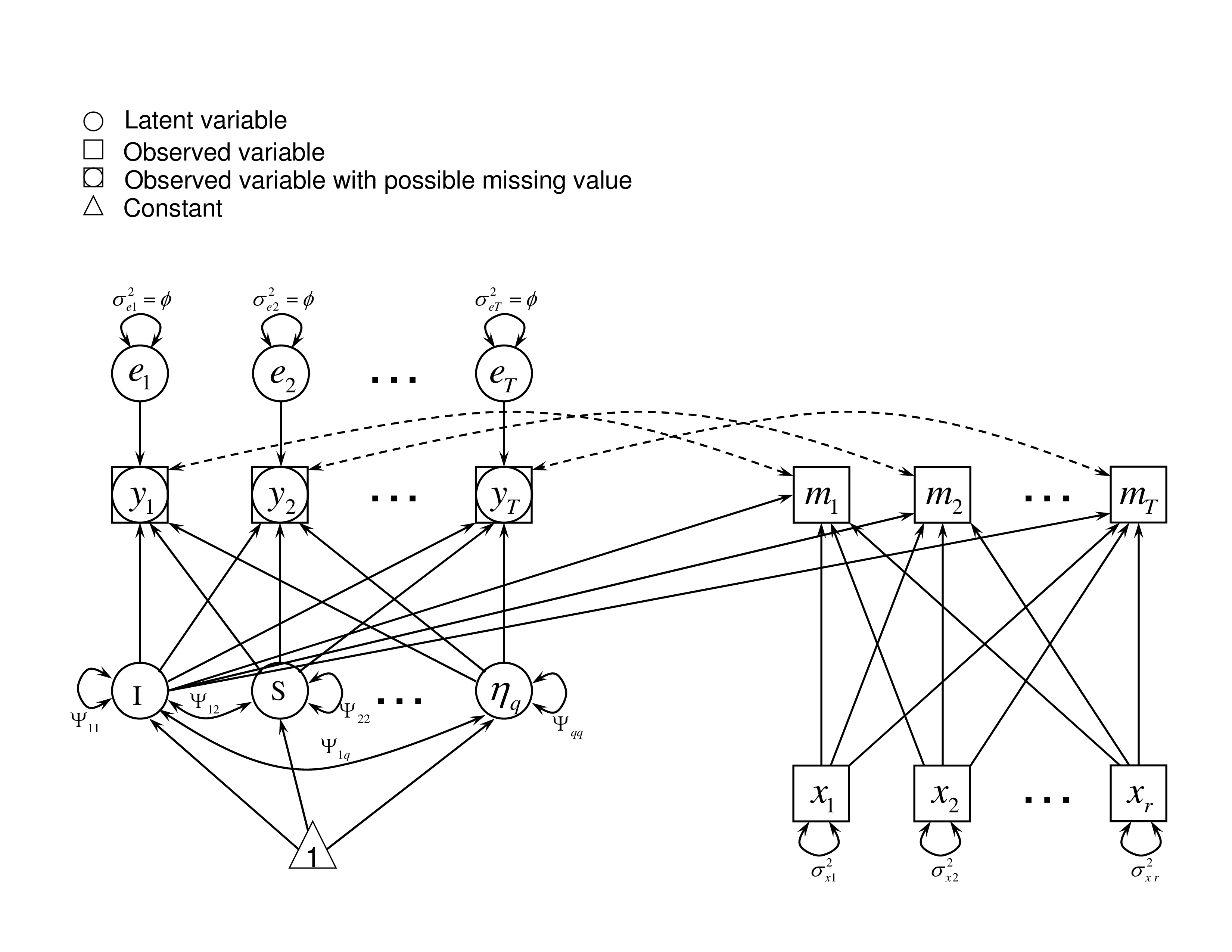
It describes the situation where the missingness depends on the latent slope, $S_{i}$. For example, a student’s latent rate of change in a course influences the likelihood that the participant misses a test in the future. This might be the case, if the student didn’t see any improvement over time, at which point he/she might choose to drop out. In the case of LSD, the $\mathbf {L}_{i}$ in Equation (3) becomes a univariate $S_{i}$. Together with some other observed covariates $\mathbf {x}_i$, for example, parents’ education or family income, the missing data rate $\tau _{it}$ can be expressed as a probit link function of $S_{i}$ and $\mathbf {x}_i$,
with $\boldsymbol {\omega }_{Si}=(1, S_{i}, \mathbf {x}_{i}')'$ and $\boldsymbol {\gamma }_{St}= (\gamma _{0t},\gamma _{St}, \boldsymbol {\gamma }_{xt}')'$. 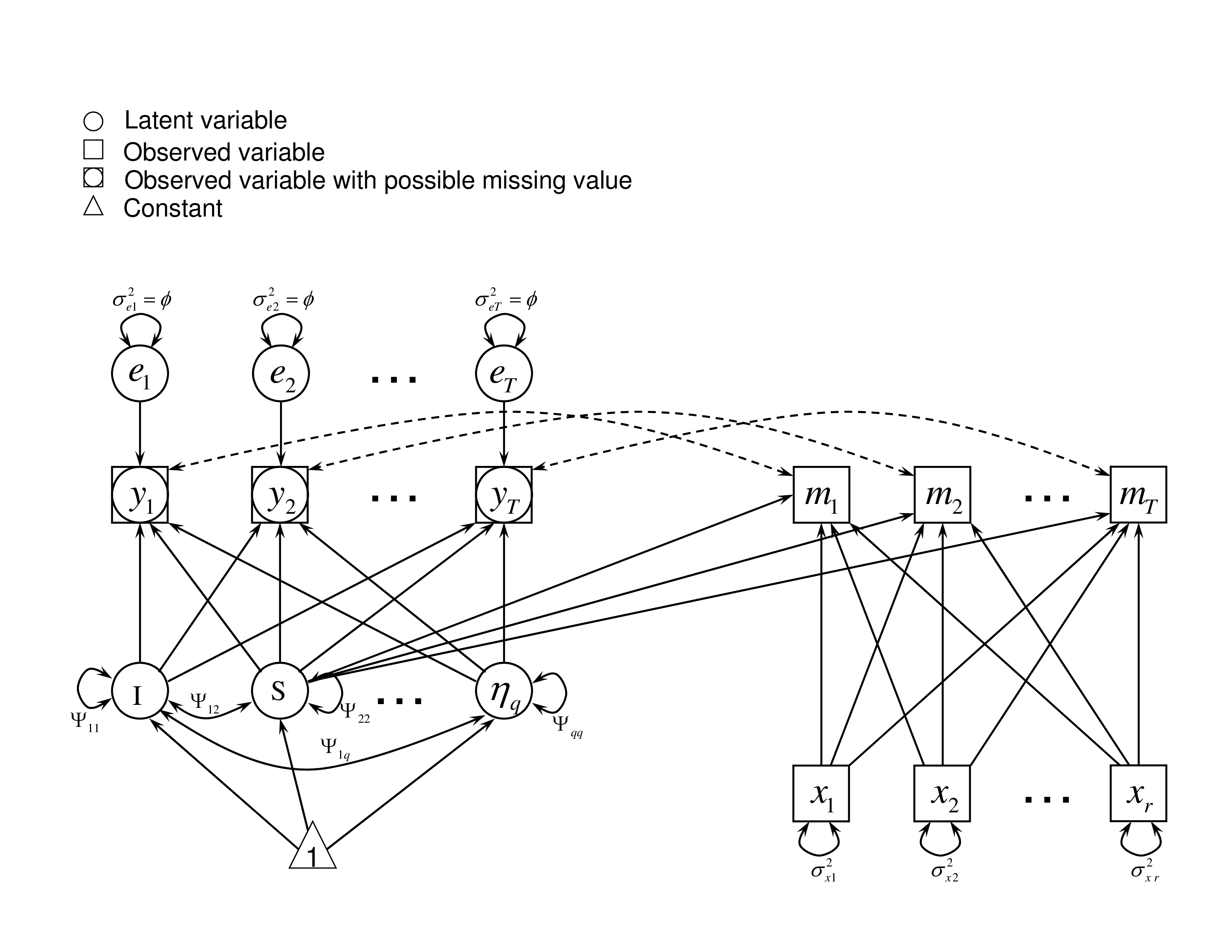
It assumes that the missingness depends on potential outcomes $y_{it}$. For example, a student who feels not doing well on a test may be more likely to quit taking the rest of the test. As a result, the missing score is due to the perceived potential outcome of the test. In this case, the $\mathbf {L}_{i}$ in Equation (3) is the potential outcome $y_{it}$. With some covariates $\mathbf {x}_i$, we express $\tau _{it}$ as a probit link function as follows.
with $\boldsymbol {\omega }_{yit}=(1, y_{it}, \mathbf {x}_{i}')'$ and $\boldsymbol {\gamma }_{yt}= (\gamma _{0t},\gamma _{yt}, \boldsymbol {\gamma }_{xt}')'$. 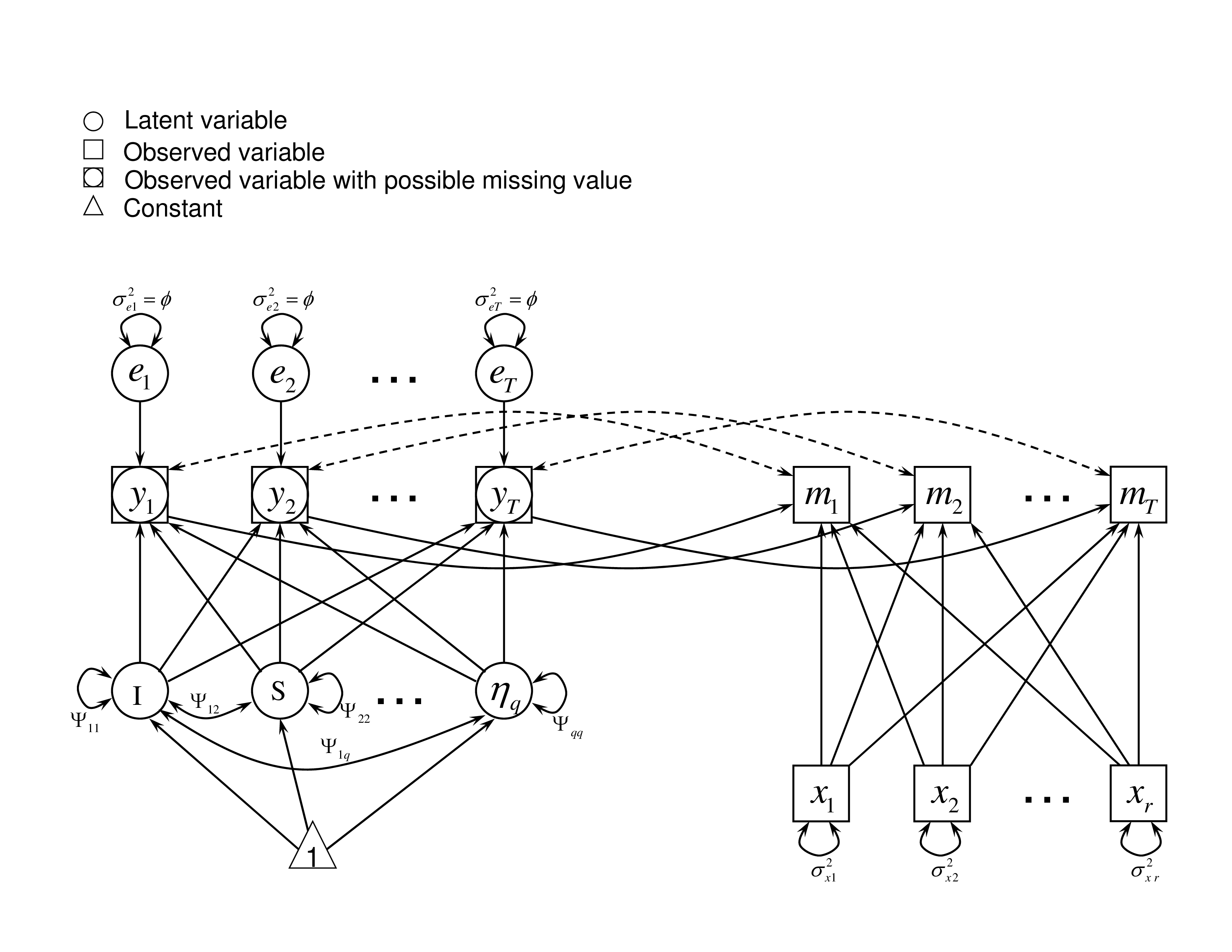
In this article, a full Bayesian estimation approach is used to estimate growth models. The algorithm is described as follows. First, model related latent variables are added via the data augmentation method (Tanner & Wong, 1987). By including auxiliary variables, the likelihood function for each model is obtained. Second, proper priors are adopted. Third, with the likelihood function and the priors, based on the Bayes’ Theorem, the posterior distribution of the unknown parameters is readily available. We obtain conditional posterior distributions instead of the joint posterior because the integrations of marginal posterior distributions of the parameters are usually hard to obtain explicitly for high-dimensional data. Fourth, with conditional posterior distributions, Markov chains are generated for the unknown model parameters by implementing a Gibbs sampling algorithm (Casella & George, 1992; Geman & Geman, 1984). Finally, statistical inference is conducted based on converged Markov chains.
In order to construct the likelihood function explicitly, we use the data augmentation algorithm (Tanner & Wong, 1987). The observed outcomes $\mathbf {y}_{i}^{obs}$ can be augmented with the missing values $\mathbf {y}_{i}^{mis}$ such that $\mathbf {y}_{i} = (\mathbf {y}_{i}^{obs}, \mathbf {y}_{i}^{mis})'$ for individual $i$. Also, the missing data indicator variable $\mathbf {m}_{i}$ is added to models. Then the joint likelihood function of the selection model for the $i^{th}$ individual can be expressed as $L_{i}(\boldsymbol {\eta }_{i},\mathbf {y}_{i},\mathbf {m}_{i})= [f(\boldsymbol {\eta }_{i}) \, f(\mathbf {y}_{i}|\boldsymbol {\eta }_{i})] \; f(\mathbf {m}_{i}|\mathbf {y}_{i},\boldsymbol {\eta }_{i},\mathbf {x}_{i})$. For the whole sample, the likelihood function is specifically expressed as
|
| (7) |
where $\tau _{it}$ is defined by Equation (4) for the LID missingness, (5) for the LSD missingness, and (6) for the LOD missingness.
The commonly used proper priors (e.g., Lee, 2007) are adopted in the study. Specifically, (1) an inverse Gamma distribution prior is used for $\phi \sim IG(v_{0}/2,s_{0}/2)$ where $v_{0}$ and $s_{0}$ are given hyper-parameters. The density function of an inverse Gamma distribution is $f(\phi ) \propto \phi ^{-(v_{0}/2)-1}\exp (-s_{0}/(2\phi ))$. (2) An inverse Wishart distribution prior is used for $\mathbf {\Psi }$. With hyper-parameters $m_{0}$ and $\mathbf {V}_{0}$, $\mathbf {\Psi } \sim IW(m_{0},\mathbf {V}_{0})$, where $m_{0}$ is a scalar and $\mathbf {V}_{0}$ is a $q\times q$ matrix. Its density function is $ f(\mathbf {\Psi })\propto |\mathbf {\Psi }|^{-(m_{0}+q+1)/2} \exp [-tr(\mathbf {V}_{0} \mathbf {\Psi }^{-1})/2]$. (3) For $\boldsymbol {\beta }$ a multivariate normal prior is used, and $\boldsymbol {\beta } \sim MN_{q}(\boldsymbol {\beta }_{0},\mathbf {\Sigma }_{0})$ where the hyper-parameter $\boldsymbol {\beta }_{0}$ is a $q$-dimensional vector and $\mathbf {\Sigma }_{0}$ is a $q \times q$ matrix. (4) The prior for $\boldsymbol {\gamma }_{t}$ ($t=1,2,\ldots ,T$) is chosen to be a multivariate normal distribution $\boldsymbol {\gamma }_{t}\sim MN_{(2+r)}(\boldsymbol {\gamma }_{t0},\mathbf {D}_{t0})$, where $\boldsymbol {\gamma }_{t0}$ is a $(2+r)$-dimensional vector, $\mathbf {D}_{t0}$ is a $(2+r) \times (2+r)$ matrix, and both are pre-determined hyper-parameters.
After constructing the likelihood function and assigning the priors, the joint posterior distribution for unknown parameters is readily available. Considering the high-dimensional integration for marginal distributions of parameters, the conditional distribution for each parameter is obtained instead. The derived conditional posteriors are provided in Equations (8) - (11) in the appendix. In addition, the conditional posteriors for the latent variable $\boldsymbol {\eta }_{i}$ and the augmented missing data $\mathbf {y}_{i}^{mis}$ ($i=1,2,...,N$) are also provided by Equations (12) and (13), respectively, in the appendix.
After obtaining the conditional posteriors, the Markov chain for each model parameter is generated by implementing a Gibbs sampling algorithm (Casella & George, 1992; Geman & Geman, 1984). Specifically, the following algorithm is used in the research.
(a) Generate $\phi ^{(s+1)}$ from the distribution in Equation (8) in the appendix.
(b) Generate $\mathbf {\Psi }^{(s+1)}$ from the inverse Wishart distribution in Equation (9) in the appendix. iv. Generate $\boldsymbol {\beta }^{(s+1)}$ from the multivariate normal distribution in Equation (10) in the appendix.
(c) Generate $\boldsymbol {\gamma }^{(s+1)}$ from the distribution in Equation (11) in the appendix.
(d) Generate $\boldsymbol {\eta }^{(s+1)}$ from the multivariate normal distribution in Equation (12) in the appendix.
(e) Generate $\mathbf {y}^{mis(s+1)}$ from the normal distribution in Equation (13) in the appendix.
After passing convergence tests, the generated Markov chains can be viewed as from the joint and marginal distributions of all parameters. The statistical inference can then be conducted based on the generated Markov chains.
Suppose $\theta $ is an unknown parameter. For different loss functions of $\theta $, the point estimates are different. For example, if a square loss function, $LF=(\theta -\hat {\theta })^2$, is used, then the posterior mean is the estimate of $\theta $; but if an absolute loss function, $LF=|\theta -\hat {\theta }|$, is used, then its estimate is the posterior median. There are other function forms, such as 0-1 loss function, but in this research we use the square loss function.
Let $\mathbf {\Theta }=(\theta _{1},\theta _{2},...,\theta _{p})'$ denote a vector of all the unknown parameters in the model. Then the converged Markov chains can be recorded as $\mathbf {\Theta }^{(s)}, s=1,2,\ldots ,S$, and each parameter estimate $\hat {\theta _{j}}$ $(j=1,2,...,p)$ can be calculated as $\hat {\theta _{j}} = \sum _{s=1}^{S}\theta _{j}^{(s)}/S $ with standard error (SE) $s.e.(\hat {\theta _{j}}) =\sqrt {\sum _{s=1}^S (\theta _{j}^{(s)} - \hat {\theta _{j}})^2 /(S-1)}$. To get the credible intervals, both percentile intervals and the highest posterior density intervals (HPD, Box & Tiao, 1973) of the Markov chains can be used. Percentile intervals are obtained by sorting $\theta _{j}^{(s)}$. HPD intervals may also be referred as minimum length confidence intervals for a Bayesian posterior distribution, and for symmetric distributions HPD intervals obtain equal tail area probabilities.
In this section, simulation studies are conducted to evaluate the performance of the proposed models estimated by the Bayesian method.
In the simulation, we focus on linear LGCMs to simplify the presentation. Higher order LGCMs can be easily expanded by adding quadratic or higher order terms.
First, four waves of complete LGCM data $\mathbf {y}_{i}$ are generated based on Equations (1) and (2). The random effects consist of the intercept $I_i$ and the slope $S_i$, with $Var(I_i)=1$, $Var(S_i)=4$, and $Cov(I_i,S_i)=0$. The fix-effects are $(I, S)=(1,3)$. The measurement errors are assumed to follow a normal distribution with mean 0 and standard deviation 1. In the simulation, we also assume there is one covariate $X$ generated from a normal distribution, $X \sim N(1, sd=0.2)$. Missing data are created based on different pre-designed missingness rates. We assume the true missingness is LSD (also noted as the XS missingness in this study because the missingness depends on the latent individual slope $S$ and covariate $X$). With LSD, the bigger the slope is, the more the missing data. For the sake of simplicity in the simulation, the missingness rate is set the same for every occasion. Specifically, we set the missingness probit coefficients as $\gamma _0=(-1,-1,-1,-1)$, $\gamma _x=(-1.5,-1.5,-1.5,-1.5)$, and $\gamma _S=(0.5,0.5,0.5,0.5)$. With the setting, missingness rates are generated based on Equation (5). If a participant has a latent growth slope 3, with a covariate value 1, his or her missingness rate at each wave is $\tau \approx 16\%$; and if the slope is 5, with the same covariate value, the missing rate increases to $\tau \approx 50\%$; but when the slope is 1, the missingness rate decreases to $\tau \approx 2.3\%$.
Next, we fit data with LGCMs with different missingness. Specifically, the model design with different missingness is shown in Table 1, where the symbol “$\checkmark $” shows the related factors on which the missing data rates depend. For example, when both “X” and “I” are checked, the missingness depends on the individual’s latent intercept “I” and the observed covariate “X”. Four types of missingness are studied: LID (also noted as XI in Table 1), LSD (XS), LOD (XY), and ignorable (X). The shaded model, LSD (XS), is the true model we used for generating the simulation data. Five levels of sample size (N=1000, N=500, N=300, N=200 and N=100) are investigated, and for each sample size. In total, 4$\times $5=20 summary tables are combined and presented in Tables 2, 3, and 5-9 2. Each result table is summarized from 100 converged replications.
Model | X5 | I6 | S7 | Y8 |
Ignorable (X) | $\checkmark $ |
|
|
|
LID2 (XI) | $\checkmark $ | $\checkmark $ |
|
|
$\checkmark $ |
| $\checkmark $ |
|
|
LOD4 (XY) | $\checkmark $ |
|
| $\checkmark $ |
Note. $^1$The shaded model is the true model XS. $^2$LID: Latent Intercept Dependent. $^3$LSD: Latent Slope Dependent. $^4$LOD: Latent Outcome Dependent. $^5$X: Observed covariates. If X is the only item checked, the missingness is ignorable. $^6$I: Individual latent intercept. If checked, the missingness is non-ignorable. $^7$S: Individual latent slope. If checked, the missingness is non-ignorable. $^8$Y: Individual potential outcome $y$. If checked, the missingness is non-ignorable.
The simulation studies are implemented by the following algorithm. (1) Set the counter $R=0$. (2) Generate complete longitudinal growth data according to predefined model parameters. (3) Create missing data according to missing data mechanisms and missing data rates. (4) Generate Markov chains for model parameters through the Gibbs sampling procedure. (5) Test the convergence of generated Markov chains. (6) If the Markov chains pass the convergence test, set $R=R+1$ and calculate and save the parameter estimates. Otherwise, set $R=R$ and discard the current replication of simulation. (7) Repeat the above process till $R=100$ to obtain 100 replications of valid simulation.
In step 4, priors carrying little prior information are adopted (Congdon, 2003; Gill, 2002; Zhang, Hamagami, Wang, Grimm, & Nesselroade, 2007). Specifically, for $\boldsymbol {\varphi }_{1}$, we set $\boldsymbol {\mu }_{\varphi _{1}} = \mathbf {0}_2$ and $\mathbf {\Sigma }_{\varphi _{1}}=10^3 \mathbf {I}_2$. For $\phi $, we set $v_{0k}=s_{0k}=0.002$. For $\boldsymbol {\beta }$, it is assumed that $\boldsymbol {\beta }_{k0}=\mathbf {0}_2$ and $\mathbf {\Sigma }_{k0} = 10^3 \mathbf {I}_2$. For $\mathbf {\Psi }$, we define $m_{k0}=2$ and $\mathbf {V}_{k0}=\mathbf {I}_2$. Finally, for $\boldsymbol {\gamma }_{t}$, we let $\boldsymbol {\gamma }_{t0}=\mathbf {0}_3$ and $\mathbf {D}_{t0}=10^3 \mathbf {I}_3$, where $\mathbf {0}_d$ and $\mathbf {I}_d$ denote a $d$-dimensional zero vector and a $d$-dimensional identity matrix, respectively. In step 5, the iteration number of burn-in period is set. The Geweke convergence criterion indicated that less than 10,000 iterations was adequate for all conditions in the study. Therefore, a conservative burn-in of 20,000 iterations was used for all iterations. And then the Markov chains with a length of $20,000$ iterations are saved for convergence testing and data analysis. After step 7, 12 summary statistics are reported based on $100$ sets of converged simulation replications. For the purpose of presentation, let $\theta _{j}$ represent the $j^{th}$ parameter, also the true value in the simulation. Twelve statistics are defined below. (1) The average estimate (est.$_{j}$) across $100$ converged simulation replications of each parameter is obtained as $\text {est.}_{j}= \bar {\hat {\theta }}_j = \sum _{i=1}^{100}\hat {\theta }_{ij}/100$, where $\hat {\theta }_{ij}$ denotes the estimate of $\theta _j$ in the $i^{th}$ simulation replication. (2) The simple bias (BIAS.smp$_{j}$) of each parameter is calculated as $\textrm {BIAS.smp}_{j} = \bar {\hat {\theta }}_j - \theta _j$. (3) The relative bias (BIAS.rel$_{j}$) of each parameter is calculated using $\textrm {BIAS.rel}_{j}=(\bar {\hat {\theta }}_j-\theta _j)/\theta _j $ when $\theta _j \neq 0$ and $\textrm {BIAS.rel}_{j}=\bar {\hat {\theta }}_j-\theta _j$ when $\theta _j=0$. (4) The empirical standard error (SE.emp$_{j}$) of each parameter is obtained as $\text {SE.emp}_{j} = \sqrt { \sum _{i=1}^{100}(\hat {\theta }_{ij}-\bar {\hat {\theta }}_j)^2 /99}$, and (5) the average standard error (SE.avg$_{j}$) of the same parameter is calculated by $\text {SE.avg}_{j} = \sum _{i=1}^{100}\hat {s}_{ij}/100$, where $\hat {s}_{ij}$ denotes the estimated standard error of $\hat {\theta }_{ij}$. (6) The average mean square error (MSE) of each parameter is obtained by $\text {MSE}_j = \sum _{i=1}^{100}\text {MSE}_{ij}/100$, where MSE$_{ij}$ is the mean square error for the $j^{th}$ parameter in the $i^{th}$ simulation replication, $\text {MSE}_{ij}=(\text {Bias}_{ij})^2 + (\hat {s}_{ij})^2$. The average lower (7) and upper (8) limits of the $95\%$ percentile confidence interval (CI.low$_j$ and CI.upper$_j$) are respectively defined as $ \text {CI.low}_{j}=\sum _{i=1}^{100} \hat {\theta }_{ij}^l/100$ and $\text {CI.upper}_{j}=\sum _{i=1}^{100} \hat {\theta }_{ij}^u/100$ where $\hat {\theta }_{ij}^l$ and $\hat {\theta }_{ij}^u$ denote the $95\%$ lower and upper limits of CI for the $j^{th}$ parameter, respectively. (9) The coverage probability of the 95% percentile confidence interval (CI.cover$_{j}$) of each parameter is obtained using $\text {CI.cover}_{j}=[\#(\hat {\theta }_{ij}^l \leq \theta _{j} \leq \hat {\theta }_{ij}^u)]/100$. The average lower (10), upper (11) limits, and (12) the coverage probability of the $95\%$ highest posterior density credible interval (HPD, Box & Tiao, 1973) of each parameter are similarly defined by HPD.low$_j$, HPD.upper$_j$, and HPD.cover$_j$, respectively.
In this section, we show simulation results for the estimates obtained from the true model and misspecified models.
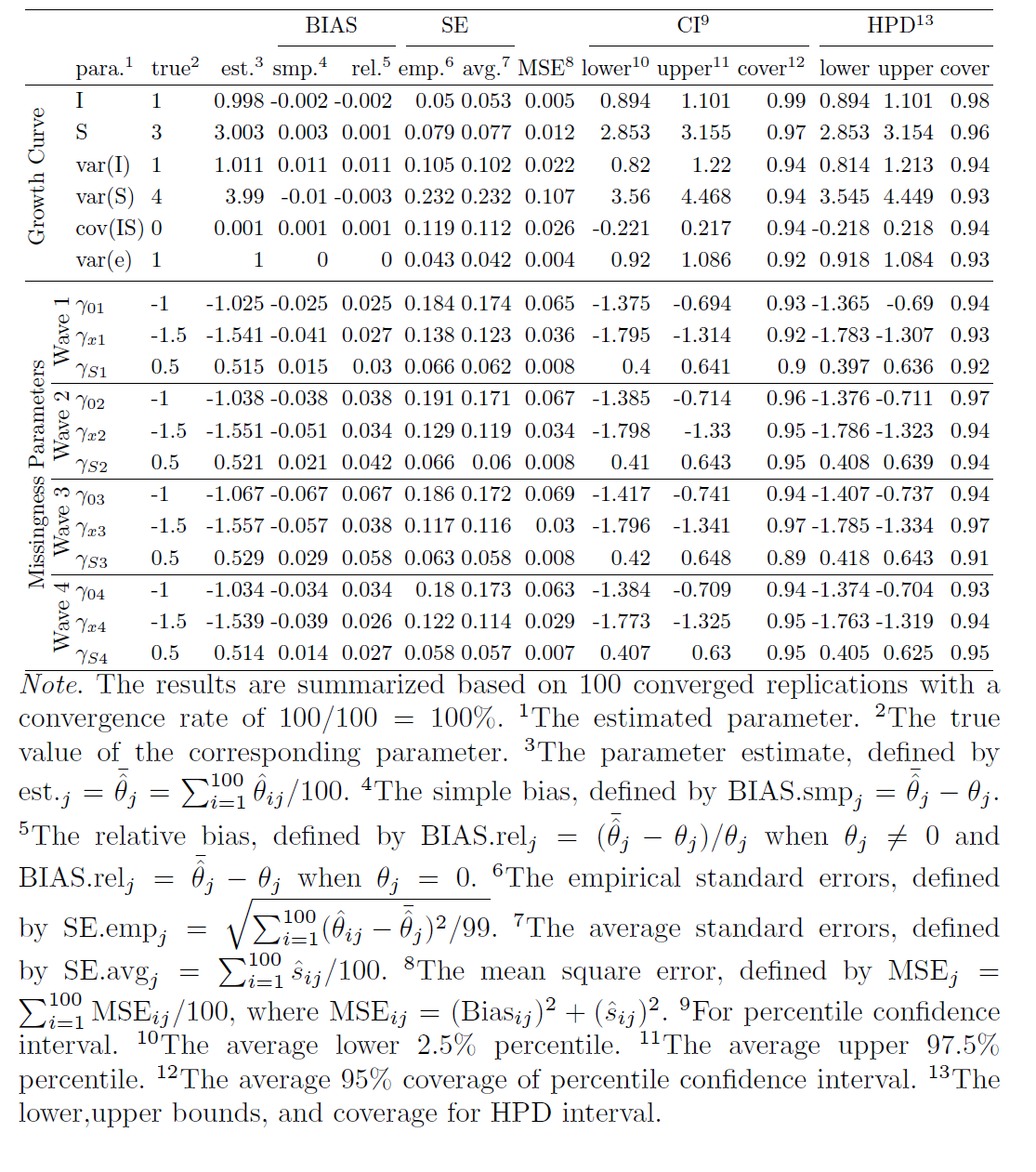
First, we investigate the estimates obtained from the true model. Tables 3, 4 and 5 in the appendix show the summarized estimates from the true model for N=1000, N=500, N=300, and N=100. From Tables 3 with the sample size 1000, first, one can see that all the relative estimate biases are very small, with the largest one being 0.067 for $\gamma _{03}$. Second, the difference between the empirical SEs and the average SEs is very small, which indicates the SEs are estimated accurately. Third, both CI and HPD interval coverage probabilities are very close to the theoretical percentage 95%, which means the type I error for each parameter is close to the specified 5% so that we can use the estimated confidence intervals to conduct statistical inference. Fourth, this true model has 100% convergence rate. When the sample sizes are smaller, the performance becomes worse as expected.
In order to compare estimates with different sample sizes, we further calculate the five summary statistics across all parameters, which are shown in Table 2. The first statistic is the average absolute relative biases ($|$Bias.rel$|$) across all parameters, which is defined as $|\text {Bias.rel}|= \sum _{j=1}^{p}|\text {Bias.rel}_{j}|/p$, where $p$ is the total number parameters in a model. Second, we obtain the average absolute differences between the empirical SEs and the average Bayesian SEs ($|$SE.diff$|$) across all parameters by using $|\text {SE.diff}|= \sum _{j=1}^{p}|\text {SE.emp}_{j}-\text {SE.avg}_{j}|/p$. Third, we calculate the average percentile coverage probabilities (CI.cover) across all parameters by using $\text {CI.cover}= \sum _{j=1}^{p}\text {CI.cover}_{j}/p$. Fourth, we calculate the average HPD coverage probabilities (HPD.cover) across all parameters by using $\text {HPD.cover}= \sum _{j=1}^{p}\text {HPD.cover}_{j}/p$. Fifth, the convergence rate is calculated.
|
| $|$Bias.rel$|$1 | $|$SE.diff$|$2 | MSE3 | CI.cover4 | HPD.cover5 | CVG.rate6 |
N | 1000 | 0.025 | 0.007 | 0.033 | 0.942 | 0.942 | 100% |
| 500 | 0.052 | 0.021 | 0.079 | 0.932 | 0.939 | 100% |
| 300 | 0.089 | 0.031 | 0.150 | 0.922 | 0.930 | 100% |
| 200 | 0.160 | 0.090 | 0.366 | 0.909 | 0.924 | 94.34% |
| 100 | 1.202 | 2.664 | 23.743 | 0.869 | 0.893 | 70.42% |
Note. $^1$The average absolute relative bias across all parameters, defined by $|\text {Bias.rel}|= \sum _{j=1}^{p}|\text {Bias.rel}_{j}|/p$. The smaller, the better. $^2$The average absolute difference between the empirical SEs and the average Bayesian SEs across all parameters, defined by $|\text {SE.diff}|= \sum _{j=1}^{p}|\text {SE.emp}_{j}-\text {SE.avg}_{j}|/p$. The smaller, the better. $^3$The Mean Square Errors (MSE) across all parameters, defined by $MSE= \sum _{j=1}^{p}[(\text {Bias}_{j})^2 + (\hat {s}_{j})^2]/p$. The smaller, the better. $^4$The average percentile coverage probability across all parameters, defined by $\text {CI.cover}= \sum _{j=1}^{p}\text {CI.cover}_{j}/p$, with a theoretical value of 0.95. $^5$The average highest posterior density (HPD) coverage probability across all parameters, defined by $\text {HPD.cover}= \sum _{j=1}^{p}\text {HPD.cover}_{j}/p$, with a theoretical value of 0.95. $^6$The convergence rate.
Table 2 shows that, except for the case for N=100, the true mode can recover model parameters very well, with small average absolute relative biases of estimates, $|$Bias.rel$|$, small average absolute differences between the empirical SEs and the average SEs, $|$SE.diff$|$, and almost 95% average percentile coverage probabilities (CI.cover), and the average HPD coverage probabilities (HPD.cover). With the increase of the sample size, both the point estimates and standard errors get more accurate.
We now compare the estimates obtained from the true model and different misspecified models. In this study, the true model is the LGCM with LSD (XS) missingness, and there are three mis-specified models, the LGCM with LID (XI) missingness, the LGCM with LOD (XY) missingness, and the LGCM with ignorable missingness (see Table 1 for the simulation design). Table 6 in the appendix shows the summarized estimates from the mis-specified model with LID (XI) missingness for N=1000, N=500, N=300, and N=200 (the summarized estimates for N=100 are unavailable due to a low convergence rate). Table 9 in the appendix provides the results for the mis-specified model with LOD (XY) missingness for N=1000, N=500, N=300, N=200, and N=100. Table 10 in the appendix is the summary table for the mis-specified model with ignorable (X) missingness for different sample sizes.
To compare estimates from different models, we further summarize and visualize some statistics. Figure 4 (a) compares the point estimates of intercept and slope for all models when N=1000. The true value of slope is 3 but the estimate is 2.711 when the missingness is ignored. Actually, for the model with ignorable missingness, the slope estimates are all less than 2.711 for all sample sizes in our study. Figure 4 (b) focuses on the coverage of slope. When the missingness is ignored, it is as low as 4% for N=1000, and 21% for N=500 (the coverage for N=1000 is lower because the SE for N=1000 is smaller than the SE for N=500). As a result, conclusions based on the model with ignorable missingness can be very misleading. Figure 4 (b) also shows that the slope estimate from the model with the mis-specified missingness, LID (XI), has low coverage, with 76% for N=1000 and 87% for N=500. So the conclusions based on this model may still be incorrect. Figure 4 (c) compares the true model and the model with another type of mis-specified missingness, LOD (XY) for N=1000. For the wrong model, the coverage is 51% for intercept, and 72% for Cov(I,S). Finally, Figure 4 (d) compares the convergence rates for all models. One can see that the convergence rates of LOD (XY) and LID (XI) models are much lower than those of the true model LSD (XS) and the model with ignorable missingness. When the missingness is ignored, the number of parameters is smaller than that of non-ignorable models, and then convergence rate gets higher.
In summary, the estimates from mis-specified models may result in misleading conclusions, especially when the missingness is ignored. Also, the convergence rate of a mis-specified model is usually lower than that of the true model.
Based on the simulation studies, we draw the following conclusions: (1) the proposed Bayesian method can accurately recover model parameters (both point estimates and standard errors), (2) the small difference between the empirical SE and the average SE indicates that the Bayesian method used in the study can estimate the standard errors accurately, (3) with the increase of the sample size, estimates get closer to their true values and standard errors become more accurate, (4) ignoring the non-ignorable missingness can lead to incorrect conclusions, (5) mis-specified missingness may also result in misleading conclusions, and (6) the non-convergence of models might be a sign of a misspecified model.
The models proposed in this article have several implications for future research. First, the missingness in the simulation study is assumed to be independent across different times. If this assumption is violated, likelihood functions might be much more complicated. For example, if the missingness depends on the previous missingness, then the autocorrelation among missingness might be involved. A similar model is the Diggle and Kenward (1994)’s model, in which the probability of missing data at current wave depends directly on the current outcomes as well as on the preceding assessment. Another example is survival analysis (e.g., Klein & Moeschberger, 2003), in which censoring is the common form of missing data problem. In practice, the missingness can come from different sources and can be modeled as a combination of different types of missingness. Second, various model selection criteria could be considered (e.g., Cain & Zhang, 2019). It is an interesting topic for future work to propose new criteria. For example, observed-data and complete-data likelihood functions for random effects models can be used for $f(\mathbf {y}|\theta )$; information criterion can be proposed using other weighted combination of the growth model and the missing data model. Third, the data considered in the study are assumed to be normally distributed. However, in reality, data are seldom normally distributed, particularly in behavioral and educational sciences (e.g., Cain, Zhang, & Yuan, 2017; Micceri, 1989). When data have heavy tails, or contaminated with outliers, robust models (e.g., Hoaglin, Mosteller, & Tukey, 1983; Huber, 1996; Zhang, 2013; Zhang, Lai, Lu, & Tong, 2013) should be adopted to make models insensitive to small deviations from the assumption of normal distribution. Fourth, latent population heterogeneity (e.g., McLachlan & Peel, 2000) may exist in the collected longitudinal data. Growth mixture models (GMMs) can be considered to provide a flexible set of models for analyzing longitudinal data with latent or mixture distributions (e.g., Bartholomew & Knott, 1999).
Acock, A. C. (2005). Working with missing values. Journal of Marriage and Family, 67, 1012-1028. doi: https://doi.org/10.1111/j.1741-3737.2005.00191.x
Allison, P. D. (2002). Missing data (sage university papers series on quantitative applications in the social sciences, 07-136). Thousands Oaks, CA: sage: Thousand Oaks, CA: SAGE publications, Inc.
Baltes, P. B., & Nesselroade, J. R. (1979). History and rationale of longitudinal research. In J. R. Nesselroade & P. B. Baltes (Eds.), Longitudinal research in the study of behavior and development (p. 1-39). New York, NY: Academic Press.
Baraldi, A. N., & Enders, C. K. (2010). An introduction to modern missing data analyses. Journal of School Psychology, 48, 5-37. doi: https://doi.org/10.1016/j.jsp.2009.10.001
Bartholomew, D. J., & Knott, M. (1999). Latent variable models and factor analysis: Kendall’s library of statistics (2nd ed., Vol. 7). New York, NY: Edward Arnold.
Box, G. E. P., & Tiao, G. C. (1973). Bayesian inference in statistical analysis. Hoboken, NJ: John Wiley & Sons.
Cain, M. K., & Zhang, Z. (2019). Fit for a bayesian: An evaluation of ppp and dic for structural equation modeling. Structural Equation Modeling: A Multidisciplinary Journal, 26(1), 39–50. doi: https://doi.org/10.1080/10705511.2018.1490648
Cain, M. K., Zhang, Z., & Yuan, K.-H. (2017). Univariate and multivariate skewness and kurtosis for measuring nonnormality: Prevalence, influence and estimation. Behavior research methods, 49(5), 1716–1735. doi: https://doi.org/10.3758/s13428-016-0814-1
Casella, G., & George, E. I. (1992). Explaining the Gibbs sampler. The American Statistician, 46(3), 167-174. doi: https://doi.org/10.1080/00031305.1992.10475878
Collins, L. (1991). Measurement in longitudinal research. In J. L. Horn & L. Collins (Eds.), Best methods for the analysis of change: Recent advances, unanswered questions, future directions (pp. 137–148). Washington, DC: American Psychological Association.
Congdon, P. (2003). Applied Bayesian modelling. Chichester, UK: John Wiley & Sons.
Dawid, A. P. (1979). Conditional independence in statistical theory. Journal of the Royal Statistical Society. Series B (Methodological), 41, 1-31. doi: https://doi.org/10.1111/j.2517-6161.1979.tb01052.x
Demidenko, E. (2004). Mixed models: Theory and applications. New York, NY: Wiley-Interscience.
Diggle, P., & Kenward, M. G. (1994). Informative drop-out in longitudinal data analysis. Journal of the Royal Statistical Society. Series C (Applied Statistics), 43, 49-93. doi: https://doi.org/10.2307/2986113
Dunson, D. B. (2000). Bayesian latent variable models for clustered mixed outcomes. Journal of the Royal Statistical Society, B, 62, 355-366. doi: https://doi.org/10.1111/1467-9868.00236
Enders, C. K. (2011a). Analyzing longitudinal data with missing values. Rehabilitation Psychology, 56, 1-22. doi: https://doi.org/10.1037/a0025579
Enders, C. K. (2011b). Missing not at random models for latent growth curve analyses. Psychological Methods, 16, 1-16. doi: https://doi.org/10.1037/a0022640
Fay, R. E. (1992). When are inferences from multiple imputation valid. In (Vol. 81, p. 227-232).
Fitzmaurice, G. M., Davidian, M., Verbeke, G., & Molenberghs, G. (Eds.). (2008). Longitudinal data analysis. Boca Raton, FL: Chapman & Hall/CRC Press.
Fitzmaurice, G. M., Laird, N. M., & Ware, J. H. (2004). Applied longitudinal analysis. Hoboken, New Jersey: John Wiley & sons Inc.
Geman, S., & Geman, D. (1984). Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence, 6, 721-741. doi: https://doi.org/10.1016/b978-0-08-051581-6.50057-x
Gill, J. (2002). Bayesian methods: A social and behavioral sciences approach. Boca Raton, FL: Chapman & Hall/CRC.
Glynn, R. J., Laird, N. M., & Rubin, D. B. (1986). Drawing inferences from self-selected samples. In H. Wainer (Ed.), (p. 115-142). New York: Springer Verlag.
Hedeker, D., & Gibbons, R. D. (1997). Application of random-effects pattern-mixture models for missing data in longitudinal studies. Psychological Methods, 2, 64-78. doi: https://doi.org/10.1037/1082-989x.2.1.64
Hedeker, D., & Gibbons, R. D. (2006). Longitudinal data analysis. Hoboken, New Jersey: John Wiley & Sons, Inc.
Hedges, L. V. (1994). Fixed effects models. In H. Cooper & L. V. Hedges (Eds.), The handbook of research synthesis. (p. 285-299). NY, US: Russell Sage Foundation.
Hoaglin, D. C., Mosteller, F., & Tukey, J. W. (1983). Understanding robust and exploratory data analysis. New York: John Wiley & Sons.
Huber, P. (1996). Robust statistical procedures (2nd ed.). Philadelphia: SIAM.
Jelicic, H., Phelps, E., & Lerner, R. M. (2009). Use of missing data methods in longitudinal studies: The persistence of bad practices in developmental psychology. Developmental Psychology, 45, 1195-1199. doi: https://doi.org/10.1037/a0015665
Klein, J. P., & Moeschberger, M. L. (2003). Survival analysis: Techniques for censored and truncated data (2nd, Ed.). Springer.
Lee, S. Y. (2007). Structural equation modeling: A Bayesian approach. Chichester, UK: John Wiley & Sons.
Little, R. J. A. (1993). Pattern-mixture models for multivariate incomplete data. Journal of the American Statistical Association, 88, 125-134. doi: https://doi.org/10.2307/2290705
Little, R. J. A. (1995). Modelling the drop-out mechanism in repeated-measures studies. Journal of the American Statistical Association, 90, 1112-1121. doi: https://doi.org/10.1080/01621459.1995.10476615
Little, R. J. A., & Rubin, D. B. (1987). Statistical analysis with missing data. New York, N.Y.: Wiley.
Little, R. J. A., & Rubin, D. B. (2002). Statistical analysis with missing data (2nd ed.). New York, N.Y.: Wiley-Interscience.
Lu, Z., Zhang, Z., & Lubke, G. (2010). (Abstract) Bayesian inference for growth mixture models with non-ignorable missing data. Multivariate Behavioral Research, 45, 1028-1029. doi: https://doi.org/10.1080/00273171.2010.534381
Lu, Z., Zhang, Z., & Lubke, G. (2011). Bayesian inference for growth mixture models with latent-class-dependent missing data. Multivariate Behavioral Research, 46, 567-597. doi: https://doi.org/10.1080/00273171.2011.589261
Luke, D. A. (2004). Multilevel modeling (quantitative applications in the social sciences). Thousand Oaks, CA: Sage Publication, Inc.
McLachlan, G. J., & Peel, D. (2000). Finite mixture models. New York, NY: John Wiley & Sons.
Micceri, T. (1989). The unicorn, the normal curve and the other improbable creatures. Psychological Bulletin, 105, 156-166. doi: https://doi.org/10.1037/0033-2909.105.1.156
Muthén, B., & Asparouhov, T. (2012). Bayesian structural equation modeling: a more flexible representation of substantive theory. Psychological methods, 17(3), 313–335. doi: https://doi.org/10.1037/a0026802
Muthén, B., Asparouhov, T., Hunter, A. M., & Leuchter, A. F. (2011). Growth modeling with nonignorable dropout: Alternative analyses of the STAR*D antidepressant trial. Psychological Methods, 16, 17-33. doi: https://doi.org/10.1037/a0022634
Newman, D. A. (2003). Longitudinal modeling with randomly and systematically missing data: A simulation of ad hoc, maximum likelihood, and multiple imputation techniques. Organizational Research Methods, 6, 328-362. doi: https://doi.org/10.1177/1094428103254673
Robert, C. P., & Casella, G. (2004). Monte Carlo statistical methods. New York, NY: Springer Science+Business Media Inc.
Roth, P. L. (1994). Missing data: A conceptual review for applied psychologists. Personnel Psychology, 47, 537-560. doi: https://doi.org/10.1111/j.1744-6570.1994.tb01736.x
Rubin, D. (1987). Multiple imputation for nonresponse in surveys. Wiley & Sons, New York.
Schafer, J. L. (1997). Analysis of incomplete multivariate data. Boca Raton, FL: Chapman & Hall/CRC.
Schafer, J. L., & Graham, J. W. (2002). Missing data: Our view of the state of the art. Psychological Methods, 7(2), 147-177. doi: https://doi.org/10.1037/1082-989x.7.2.147
Scheines, R., Hoijtink, H., & Boomsma, A. (1999). Bayesian estimation and testing of structural equation models. Psychometrika, 64, 37-52. doi: https://doi.org/10.1007/bf02294318
Schlomer, G. L., Bauman, S., & Card, N. A. (2010). Best practices for missing data management in counseling psychology. Journal of Counseling Psychology, 57, 1-10. doi: https://doi.org/10.1037/a0018082
Singer, J. D., & Willett, J. B. (2003). Applied longitudinal data analysis: Modeling change and event occurrence. New York, NY: Oxford University Press, Inc.
Tanner, M. A., & Wong, W. H. (1987). The calculation of posterior distributions by data augmentation. Journal of the American Statistical Association, 82, 528-540. doi: https://doi.org/10.1080/01621459.1987.10478458
Yuan, K.-H., & Lu, Z. (2008). SEM with missing data and unknown population using two-stage ML: theory and its application. Multivariate Behavioral Research, 43, 621-652. doi: https://doi.org/10.1080/00273170802490699
Yuan, K.-H., & Zhang, Z. (2012). Robust structural equation modeling with missing data and auxiliary variables. Psychometrika, 77(4), 803-826. doi: https://doi.org/10.1007/s11336-012-9282-4
Zhang, Z. (2013). Bayesian growth curve models with the generalized error distribution. Journal of Applied Statistics, 40(8), 1779–1795. doi: https://doi.org/10.1080/02664763.2013.796348
Zhang, Z., Hamagami, F., Wang, L., Grimm, K. J., & Nesselroade, J. R. (2007). Bayesian analysis of longitudinal data using growth curve models. International Journal of Behavioral Development, 31(4), 374-383. doi: https://doi.org/10.1177/0165025407077764
Zhang, Z., Lai, K., Lu, Z., & Tong, X. (2013). Bayesian inference and application of robust growth curve models using student’s t distribution. Structural Equation Modeling, 20(1), 47-78. doi: https://doi.org/10.1080/10705511.2013.742382
Zhang, Z., & Wang, L. (2012). A note on the robustness of a full bayesian method for non-ignorable missing data analysis. Brazilian Journal of Probability and Statistics, 26(3), 244-264. doi: https://doi.org/10.1214/10-bjps132
Let $\boldsymbol {\eta }=(\boldsymbol {\eta }_{1}, \boldsymbol {\eta }_{2}, \ldots , \boldsymbol {\eta }_{N})$, and the conditional posterior distribution for $\phi $ can be easily derived as an Inverse Gamma distribution,
where $a_{1}=v_{0}+N\,T$, and $b_{1}=s_{0}+\sum _{i=1}^N (\mathbf {y}_{i}-\mathbf {\Lambda } \boldsymbol {\eta }_{i})'(\mathbf {y}_{i}-\mathbf {\Lambda } \boldsymbol {\eta }_{i})$.Notice that $tr(\mathbf {AB})=tr(\mathbf {BA})$, so the conditional posterior distribution for $\mathbf {\Psi }$ is derived as an Inverse Wishart distribution,
where $m_{1}=m_{0}+N$, and $\mathbf {V}_{1}=\mathbf {V}_{0}+\sum _{i=1}^N(\boldsymbol {\eta }_{i}-\boldsymbol {\beta })(\boldsymbol {\eta }_{i}-\boldsymbol {\beta })'$.By expanding the terms inside the exponential part and combining similar terms, the conditional posterior distribution for $\boldsymbol {\beta }$ is derived as a multivariate normal distribution,
where $\boldsymbol {\beta }_{1}=\left (N\,\mathbf {\Psi }^{-1}+\mathbf {\Sigma }_{0}^{-1}\right )^{-1}\left (\mathbf {\Psi }^{-1} \sum _{i=1}^N\boldsymbol {\eta }_{i}+\mathbf {\Sigma }_{0}^{-1}\boldsymbol {\beta }_{0}\right )$, and $\mathbf {\Sigma }_{1}=\left (N\,\mathbf {\Psi }^{-1}+\mathbf {\Sigma }_{0}^{-1}\right )^{-1}$.The conditional posterior for $\boldsymbol {\gamma }_{t}$, $(t=1,2,\ldots ,T)$, is a distribution of
|
| (11) |
where $\Phi (\boldsymbol {\omega }_{i}'\boldsymbol {\gamma }_{t})$ is defined by Equation (4), (5), or (6).
By expanding the terms inside the exponential part and combining similar terms, the conditional posterior distribution for $\boldsymbol {\eta }_{i}$, $i=1,2,\ldots ,N$, is derived as a Multivariate Normal distribution,
|
| (12) |
where $\boldsymbol {\mu }_{\eta i}=\left (\frac {1}{\phi }\mathbf {\Lambda }'\mathbf {\Lambda } + \mathbf {\Psi }^{-1} \right )^{-1} \left (\frac {1}{\phi } \mathbf {\Lambda }'\mathbf {y}_{i}+ \mathbf {\Psi }^{-1}\boldsymbol {\beta } \right )$, and $\mathbf {\Sigma }_{\eta i}=\left (\frac {1}{\phi }\mathbf {\Lambda }'\mathbf {\Lambda } + \mathbf {\Psi }^{-1} \right )^{-1}$.
The conditional posterior distribution for the missing data $\mathbf {y}_{i}^{mis}$, $i=1,2,\ldots ,N$, is a normal distribution,
where $\mathbf {I}$ is a $T\times T$ identity matrix. The dimension and location of $\mathbf {y}_{i}^{mis}$ depend on the corresponding $\mathbf {m}_{i}$ value.
1 Throughout the article, $MN_n(\cdot )$ denotes a $n$-dimensional multivariate normal distribution, and $Mt_n(\cdot )$ denotes a $n$-dimensional multivariate t distribution.
2 The summary table for the model with the latent intercept dependent (LID) missingness (XI), for N=100 is not included due to its low convergence rate.