Keywords: Growth Mixture Models · Nonlinear Trajectories · Individual Measurement Occasions · Covariates · Simulation Studies · Exploratory Factor Analysis
Earlier studies have examined the impacts of time-invariant covariates (TICs) on nonlinear mathematics achievement trajectories. For example, Liu, Perera, Kang, Kirkpatrick, and Sabo (2019) associated nonlinear change patterns of mathematics IRT scaled scores to baseline covariates, including demographic information, socioeconomics factors, and school information. With the assumption that all covariates explain sample variability directly, this study showed that some baseline characteristics, such as sex, school type, family income, and parents’ highest education, can explain the heterogeneity in the nonlinear trajectories of mathematics scores. However, Kohli, Hughes, Wang, Zopluoglu, and Davison (2015) showed that latent classes of change patterns of mathematics achievement exist. Accordingly, these covariates may also inform latent class formation. In this study, we want to investigate the indirect impacts the baseline characteristics have on sample heterogeneity.
The finite mixture model (FMM) represents heterogeneity in a sample by allowing for a finite number of latent (unobserved) classes. The idea of mixture models is to put multiple probability distributions together using a linear combination. Although researchers may want to consider two different or multiple different families for the different kernels in some circumstances, the assumption that all latent classes’ probability density functions follow normal distributions with class-specific parameters is common in application.
This framework has gained considerable attention in the past twenty years among social and behavioral scientists due to its advantages over other clustering algorithms such as K-means for investigating sample heterogeneity. First, in the SEM framework, the FMM can incorporate any form of within-class models. For instance, Lubke and Muthén (2005) specified factor mixture models, where the within-class model is a factor model to investigate heterogeneity in common factors. In contrast, Muthén and Shedden (1999) defined growth mixture models (GMM), where the within-class model is a latent growth curve model to examine heterogeneity in trajectories. More importantly, the FMM is a model-based clustering method (Bouveyron, Celeux, Murphy, & Raftery, 2019) so that researchers can specify a model in this framework with domain knowledge: which parameters can be fixed to specific values, which need to be estimated, and which can be constrained to be equal (for example, invariance across classes). Additionally, the FMM is a probability-based clustering approach. Unlike other clustering methods, such as the K-means clustering algorithm, which aims to separate all observations into several clusters so that each entry belongs to one cluster without considering uncertainty, the FMM allows each element to belong to multiple classes simultaneously.
This article focuses on the GMM with a nonlinear latent growth curve model as the within-class model. Specifically, trajectories in each class in the proposed GMM is a linear-linear piecewise model (Harring, Cudeck, & du Toit, 2006; Kohli, 2011; Kohli & Harring, 2013; Kohli, Harring, & Hancock, 2013; Kohli et al., 2015; Sterba, 2014), also referred to as a bilinear growth model (Grimm, Ram, & Estabrook, 2016; Liu, 2019; Liu et al., 2019) with an unknown change-point (or knot). We decide to use the bilinear spline functional form for two considerations. First, in addition to examining the growth rate of each stage directly, this piecewise function allows for estimating the transition time from one stage to the other. Additionally, Kohli et al. (2015) and Liu et al. (2019), have shown that a growth model with this functional form can capture the underlying change patterns of mathematics achievement and outperforms several parametric functions: linear, quadratic, and Jenss-Bayley from the statistical perspective.
Similar to Liu et al. (2019), we propose the model in the framework of individual measurement occasions to account for possible heterogeneity in the measurement time in longitudinal studies (Cook & Ware, 1983; Finkel, Reynolds, Mcardle, Gatz, & Pedersen, 2003; Mehta & West, 2000). Earlier studies, for example, (Preacher & Hancock, 2015; Sterba, 2014) have demonstrated one possible solution to individual measurement occasions is to place the exact time to the matrix of factor loadings, termed the definition variable approach (Mehta & Neale, 2005; Mehta & West, 2000). Earlier studies have shown that the definition variable approach outperforms some approximate methods such as the time-bins approach (where the assessment period is divided into several bins, and the factor loadings are set as those time-bins) in terms of bias, efficiency, and Type I error rate (Blozis & Cho, 2008; Coulombe, Selig, & Delaney, 2015).
Many studies in the SEM framework start from an exploratory stage where even empirical researchers only have vague assumptions about sample heterogeneity and possible reasons. It suggests that we usually have two challenges when implementing a FMM, deciding the number of latent classes and selecting which covariates need to be included in the model. To investigate which criterion can be used to decide the number of latent classes, Nylund, Asparouhov, and Muthén (2007) evaluated the performance of likelihood-based tests and the traditionally used information criteria and showed that the bootstrap likelihood ratio test is a consistent indicator while the Bayesian information criterion (BIC) performs the best among all information criteria. Note that in practice, the BIC, which is calculated from the estimated likelihood directly, is usually more favorable due to its computational efficiency.
It is also challenging to decide to include which covariates as predictors of class membership. Previous studies have shown that including subject-level predictors for latent classes can be realized by either one-step models (Bandeen-Roche, Miglioretti, Zeger, & Rathouz, 1997; Clogg, 1981; Dayton & Macready, 1988; Goodman, 1974; Haberman, 1979; Hagenaars, 1993; Kamakura, Wedel, & Agrawal, 1994; Vermunt, 1997; Yamaguchi, 2000), two-step models (Bakk & Kuha, 2017) or three-step models (Asparouhov & Muthén, 2014; Bolck, Croon, & Hagenaars, 2004; Vermunt, 2010). The one-step model is suitable if a study is conducted in a confirmatory way or driven by answering a particular question, where specifying a proper mixture model for the covariates is usually a knowledge-driven process. On the contrary, the stepwise model is more suitable for an exploratory study in which empirical researchers usually have limited a priori knowledge about possible class structure. For such studies, the current recommended approach is to investigate the number and nature of the clusters without adding any covariates so that they do not inform class formation.
In this study, we utilize the two-step model given that a considerable number of studies investigated in the SEM framework start from the exploratory stage and that Bakk and Kuha (2017) has shown that the two-step procedure is consistently better than the three-step approach as it does not ignore the presence of uncertainty in the modal class assignments. Accordingly, by extending the method proposed in Bakk and Kuha (2017) to the FMM with a bilinear spline growth curve as the within-class model, we first group nonlinear trajectories and estimate class-specific parameters with a pre-specified number of clusters by fitting the measurement-model portion of the mixture model; we then investigate the associations between the ‘soft clusters’, where each sample is assigned with different posterior weights, and the individual-level covariates by fitting the measurement and structural model but fixing the measurement parameter estimates as their values from the first step. By utilizing the two-step model, we only need to refit the model in the second step rather than the whole model when adding or removing covariates, saving the computational budget.
However, the covariate space in the psychological and educational domains where the SEM framework is widely utilized is usually large, and some covariates are highly correlated. To address this issue, we propose to leverage a common multivariate data analysis approach in the SEM framework, exploratory factor analysis (EFA), to reduce the covariate space’s dimension and address potential multicollinearity. Note that in this current study, it is not our aim to examine EFA comprehensively. We only want to demonstrate how to use the individual scores, for example, Thompson’s scores (Thomson, 1939), or Bartlett’s weighted least-squares scores (Bartlett, 1937), based on the output of EFA, with a basic understanding of its algorithm.
EFA is a useful multivariate data analysis approach to explain the variance-covariance matrix of the dataset by replacing a large set of manifest variables with a smaller latent variable set. In this approach, manifested variables are assumed to be caused by latent variables. When implementing EFA, we impose no constraints on the relationships between manifested and latent variables. Assuming that all manifested variables are related to all latent variables, this approach aims to determine the appropriate number of factors and factor loadings (i.e., correlations between observed variables and unobserved variables). Next, we calculate a score for each factor of each individual based on the factor loadings and standardized covariate values. We then view these individual-level scores instead of the covariates as baseline characteristics in the second step.
The proposed hybrid method aims to provide an analytical framework for examining heterogeneity in an exploratory study. We extend the two-step method proposed by Bakk and Kuha (2017) to investigate the heterogeneity in nonlinear trajectories in the framework of individually varying time points (ITPs). Specifically, we consider the bilinear spline growth curve with an unknown knot as the within-class model. We specify the model with truly individual measurement occasions, which are ubiquity in longitudinal studies, to avoid unnecessary inadmissible estimation. Additionally, we propose to use EFA to reduce the dimension of the covariate space.
The remainder of this article is organized as follows. We describe the model specification and model estimation of the two-step growth mixture model in the framework of ITPs in the method section. In the subsequent section, we describe the design of the Monte Carlo simulation for model evaluation. We evaluate the model performance through the performance measures, which include the relative bias, the empirical standard error (SE), the relative root-mean-squared-error (RMSE), and the empirical coverage for a nominal $95\%$ confidence interval of each parameter of interest, as well as accuracy. We then introduce the dataset of repeated mathematics achievement scores from the Early Childhood Longitudinal Study, Kindergarten Class of 2010-11 (ECLS-K: 2011), and demonstrate the implementation of the hybrid method in the application section. Finally, discussions are framed concerning methodological considerations and future directions.
In this section, we specify the GMM with a bilinear spline growth curve as the within-class model. Harring et al. (2006) showed there are five parameters in the bilinear spline functional form: an intercept and slope of each linear piece and a change-point, yet the degree of freedom of the bilinear spline is four since two linear pieces join at the knot. In this study, we view the initial status, two slopes, and the knot as the four parameters. We construct the model with consideration of the variability of the initial status and two slopes, but assuming that the class-specific knot is the same across all individuals in a latent class though Liu et al. (2019); Preacher and Hancock (2015) have shown that the knot can also have a random effect by relaxing the assumption. Suppose the pre-specified number of latent classes is $K$, for $i=1$ to $n$ individuals and $k=1$ to $K$ latent classes, we express the model as
Equation (1) defines a FMM that combines mixing proportions, $\pi (z_{i}=k|\boldsymbol {x}_{i})$, and within-class models, $p(\boldsymbol {y}_{i}|z_{i}=k)$, where $\boldsymbol {x}_{i}$, $\boldsymbol {y}_{i}$ and $z_{i}$ are the covariates, $J\times 1$ vector of repeated outcome (where $J$ is the number of measurements) and membership of the $i^{th}$ individual, respectively. For Equation (1), we have two constratints: $0\le \pi (z_{i}=k|\boldsymbol {x}_{i})\le 1$ and $\sum _{k=1}^{K}\pi (z_{i}=k|\boldsymbol {x}_{i})=1$. Equation (2) defines mixing components as logistic functions of covariates $\boldsymbol {x}_{i}$, where $\beta _{0}^{(k)}$ and $\boldsymbol {\beta }^{(k)}$ are the class-specific logistic coefficients. These functions decide the membership for the $i^{th}$ individual, depending on the values of the covariates $\boldsymbol {x}_{i}$.
Equations (3) and (4) together define a within-class model. Similar to all factor models, Equation (3) expresses the outcome $\boldsymbol {y}_{i}$ as a linear combination of growth factors. When the underlying functional form is bilinear spline growth curve with an unknown fixed knot, $\boldsymbol {\eta }_{i}$ is a $3\times 1$ vector of growth factors ($\boldsymbol {\eta }_{i}=\eta _{0i},\eta _{1i},\eta _{2i}$, for an initial status and a slope of each stage of the $i^{th}$ individual). Accordingly, $\boldsymbol {\Lambda }_{i}(\gamma ^{(k)})$, which is a function of the class-specific knot $\gamma ^{(k)}$, is a $J\times 3$ matrix of factor loadings. Note that the subscript $i$ in $\boldsymbol {\Lambda }_{i}(\gamma ^{(k)})$ indicates that it is a function of the individual measurement occasions of the $i^{th}$ individual. The pre- and post-knot $\boldsymbol {y}_{i}$ can be expressed as
|
|
where $y_{ij}$ and $t_{ij}$ are the measurement and measurement occasion of the $i^{th}$ individual at time $j$. Additionally, $\boldsymbol {\epsilon }_{i}$ is a $J\times 1$ vector of residuals of the $i^{th}$ individual. Equation (4) further expresses the growth factors as deviations from their class-specific means. In the equation, $\boldsymbol {\mu _{\eta }}^{(k)}$ is a $3\times 1$ vector of class-specific growth factor means and $\boldsymbol {\zeta }_{i}$ is a $3\times 1$ vector of residual deviations from the mean vector of the $i^{th}$ individual.
To unify pre- and post-knot expressions, we need to reparameterize growth factors. Earlier studies, for example, Grimm et al. (2016); Harring et al. (2006); Liu et al. (2019), presented multiple ways to realize this aim. Note that no matter which approach we follow to reparameterize growth factors, the reparameterized coefficients are not directly related to the underlying change patterns and need to be transformed back to be interpretable. In this article, we follow the reparameterized method in Liu et al. (2019) and define the class-specific reparameterized growth factors as the measurement at the knot, mean of two slopes, and the half difference of two slopes. Note that the expressions of the repeated outcome $\boldsymbol {y}_{i}$ using the growth factors in the original and reparameterized frames are equivalent. We also extend the (inverse-)transformation functions and matrices for the reduced model in Liu et al. (2019), with which we can obtain the original parameters efficiently for interpretation purposes. Detailed class-specific reparameterizing process and the class-specific (inverse-) transformation are provided in Appendix 6.2 and Appendix 6.2, respectively.
To simplify the model, we assume that class-specific growth factors follow a multivariate Gaussian distribution, that is, $\boldsymbol {\zeta }_{i}|k\sim \text {MVN}(\boldsymbol {0}, \boldsymbol {\Psi _{\eta }}^{(k)})$. Note that $\boldsymbol {\Psi _{\eta }}^{(k)}$ is a $3\times 3$ variance-covariance matrix of class-specific growth factors. We also assume that individual residuals follow identical and independent normal distributions over time in each latent class, that is, $\boldsymbol {\epsilon }_{i}|k\sim N(\boldsymbol {0}, \theta _{\epsilon }^{(k)}\boldsymbol {I})$, where $\boldsymbol {I}$ is a $J\times J$ identity matrix. Accordingly, for the $i^{th}$ individual in the $k^{th}$ unobserved group, the within-class model implied mean vector ($\boldsymbol {\mu }_{i}^{(k)}$) and variance-covariance matrix ($\boldsymbol {\Sigma }_{i}^{(k)}$) of repeated measurements are
In the first step, we estimate the class-specific parameters and mixing proportions for the model specified in Equations (1), (2), (3) and (4) without considering the impact that covariates $\boldsymbol {x}_{i}$ have on the class formation. The parameters need to be estimated in this step include
|
|
We employ full information maximum likelihood (FIML) technique, which accounts for the potential heterogeneity of individual contributions to the likelihood, to estimate $\boldsymbol {\Theta }_{s1}$. The log-likelihood function of the model specified in Equations (1), (2), (3) and (4) without the effect of $\boldsymbol {x}_{i}$ is
|
| (7) |
In the second step, we examine the associations between the ‘soft clusters’, where each trajectory is assigned with different posterior probabilities, and the baseline characteristics by fixing the class-specific parameters as their estimates from the first step, that is, the parameters need to be estimated in this step are those logistic coefficients, $\boldsymbol {\Theta }_{\text {s2}}=\{\beta _{0}^{(k)}, \boldsymbol {\beta }^{T(k)}\boldsymbol {}\}\ (k=2,\dots ,K$), in Equation (2). The log-likelihood function in Equation (7) also needs to be modified as
|
| (8) |
We construct the proposed two-step GMM using the R package OpenMx with the optimizer CSOLNP (Boker et al., 2020; Hunter, 2018; Neale et al., 2016; Pritikin, Hunter, & Boker, 2015), with which we can fit the proposed GMM and implement the class-specific inverse-transformation matrices to obtain coefficients that are directly related to underlying change patterns as shown in Appendix 6.2. In the online appendix (https://github.com/Veronica0206/Dissertation\_projects), we provide the OpenMx code for the proposed model as well as a demonstration. For the researchers interested in using Mplus, we also provide Mplus 8 code for the model in the online appendix.
We evaluate the proposed model using a Monte Carlo simulation study with two goals. The first goal is to evaluate the model performance by examining the relative bias, empirical SE, relative RMSE, and empirical coverage for a nominal 95% confidence interval (CI) of each parameter. Table 1 lists the definitions and estimates of these performance metrics.
| Criteria | Definition | Estimate |
| Relative Bias | $E_{\hat {\theta }}(\hat {\theta }-\theta )/\theta $ | $\sum _{s=1}^{S}(\hat {\theta }_{s}-\theta )/S\theta $ |
| Empirical SE | $\sqrt {Var(\hat {\theta })}$ | $\sqrt {\sum _{s=1}^{S}(\hat {\theta }_{s}-\bar {\theta })^{2}/(S-1)}$ |
| Relative RMSE | $\sqrt {E_{\hat {\theta }}(\hat {\theta }-\theta )^{2}}/\theta $ | $\sqrt {\sum _{s=1}^{S}(\hat {\theta }_{s}-\theta )^{2}/S}/\theta $ |
| Coverage Probability | $Pr(\hat {\theta }_{\text {low}}\le \theta \le \hat {\theta }_{\text {upper}})$ | $\sum _{s=1}^{S}I(\hat {\theta }_{\text {low},s}\le \theta \le \hat {\theta }_{\text {upper},s})/S$ |
The second goal is to evaluate how well the clustering algorithm performs to separate the heterogeneous trajectories. To evaluate the clustering effects, we need to calculate the posterior probabilities for each individual belonging to the $k^{th}$ unobserved group. The calculation is based on the class-specific estimates and mixing proportions obtained from the first step and realized by Bayes’ theorem
|
|
We then assign each individual to the latent class with the highest posterior probability to which that observation most likely belongs. If multiple posterior probabilities equal to the maximum value, we break the tie among competing components randomly (McLachlan & Peel, 2000). We evaluate the clustering effects by accuracy and entropy. Since the true membership is available in simulation studies, we are able to calculate accuracy, which is defined as the fraction of all correctly labeled instances (Bishop, 2006). Entropy, which is given
|
| (9) |
is a metric based on the average posterior probabilities (Stegmann & Grimm, 2018). It ranges from $0$ to $1$, where $0$ and $1$ suggesting no cluster separation and complete separation, respectively. It is an indicator of the quality of the mixture model. In the current study, entropy reflects separation only based on the trajectories as shown in Equation (9). Earlier studies, for example, Lubke and Muthén (2007), have demonstrated that entropy is a good indicator of accuracy when we exclude all covariates from the mixture model. It is our interest to test the robustness of this recommendation in the context of the growth mixture model with nonlinear trajectories.
We decided the number of repetitions $S=1,000$ by an empirical approach proposed by Morris, White, and Crowther (2019) in the simulation design. The (relative) bias is the most important performance metric in our simulation, so we want to keep its Monte Carlo standard error3 less than $0.005$. We ran a pilot simulation study and noted that standard errors of all parameters except the intercept variances were less than $0.15$, so we needed at least $900$ replications to ensure the Monte Carlo standard error of bias is as low as we expected. We then decided to proceed with $S=1,000$ to be more conservative.
The simulation study has two parts. As mentioned earlier, we propose the two-step model with a bilinear spline growth curve with an unknown knot as the within-class model, assuming that the change-point is roughly similar for all individuals in each latent class as the knot variance is not the primary interest of this study. In the first part, we restricted the knot to be identical for all trajectories in a latent class to evaluate the model performance when being specified correctly. We are also interested in examining how the proposed model works when relaxing the restriction. Accordingly, in the second part, by allowing for the individual difference in the knot, we investigated the robustness of the proposed model by assessing the model performance in the presence of knots with the standard deviation set as $0.3$.
We list all conditions of simulation studies for Part 1 and Part 2 in Table 2. All conditions except the knot variance for both parts were set to be the same. For both parts, we fixed the conditions that are not of the primary interests of the current study. For example, we considered ten scaled and equally-spaced waves since Liu et al. (2019) has shown that the bilinear growth model had decent performance concerning the performance measures to a longitudinal data set with ten repeated measures and fewer number of measurements only affected model performance slightly. Similar to Liu et al. (2019), we allowed the time-window of individual measurement occasions ranging from $-0.25$ and $+0.25$, which was viewed as a ‘medium’ deviation, as an existing simulation study (Coulombe et al., 2015), around each wave. We also fixed the variance-covariance matrix of the class-specific growth factors that usually change with the time scale and the measurement scale in practice; accordingly, we kept the index of dispersion ($\sigma ^{2}/\mu $) of each growth factor at the one-tenth scale, guided by Bauer and Curran (2003); Kohli (2011); Kohli et al. (2015). Further, the growth factors were set to be positively correlated to a moderate degree ($\rho =0.3$).
| Fixed Conditions | ||
Variables | Conditions
| |
Variance of Intercept | $\psi _{00}^{(k)}=25$
| |
Variance of Slopes | $\psi _{11}^{(k)}=\psi _{22}^{(k)}=1$
| |
Correlations of GFs | $\rho ^{(k)}=0.3$
| |
Time (t) | $10$ scaled and equally spaced $t_{j} (j=0, \cdots , J-1, J=10)$
| |
Individual t | $t_{ij} \sim U(t_{j}-\Delta , t_{j}+\Delta ) (j=0, \cdots , J-1; \Delta =0.25)$ | |
| Manipulated Conditions
| ||
Variables | 2 latent classes | 3 latent classes |
Sample Size | $n=500$ or $1000$ | $n=500$ or $1000$ |
Variance of Knots | $\psi _{\gamma \gamma }^{(k)}=0.00 (k = 1, 2)$ | $\psi _{\gamma \gamma }^{(k)}=0.00 (k = 1, 2, 3)$ |
| $\psi _{\gamma \gamma }^{(k)}=0.09 (k = 1, 2)$ | $\psi _{\gamma \gamma }^{(k)}=0.09 (k = 1, 2, 3)$ |
Ratio of Proportions | $\pi ^{(1)}:\pi ^{(2)}=1:1$ | $\pi ^{(1)}:\pi ^{(2)}:\pi ^{(3)}=1:1:1$ |
| $\pi ^{(1)}:\pi ^{(2)}=1:2$ | $\pi ^{(1)}:\pi ^{(2)}:\pi ^{(3)}=1:1:2$ |
|
| $\pi ^{(1)}:\pi ^{(2)}:\pi ^{(3)}=1:2:2$ |
Residual Variance | $\theta _{\epsilon }^{(k)}=1$ or $2$ | $\theta _{\epsilon }^{(k)}=1$ or $2$ |
Locations of knots | $\mu _{\gamma }=(4.00, 5.00)$ | $\mu _{\gamma }=(3.50, 4.50, 5.50)$ |
| $\mu _{\gamma }=(3.75, 5.25)$ | $\mu _{\gamma }=(3.00, 4.50, 6.00)$ |
| $\mu _{\gamma }=(3.50, 5.50)$ |
|
Mahalanobis distance | $d=0.86$ or $1.72$ | $d=0.86$ |
Scenario 1: Different means of initial status and (means of) knot locations
| ||
Variables | 2 latent classes | 3 latent classes |
Means of Slope 1’s | $\mu _{\eta _{1}}^{(k)}=-5$ $(k=1, 2)$ | $\mu _{\eta _{1}}^{(k)}=-5$ $(k=1, 2, 3)$ |
Means of Slope 2’s | $\mu _{\eta _{2}}^{(k)}=-2.6$ $(k=1, 2)$ | $\mu _{\eta _{2}}^{(k)}=-2.6$ $(k=1, 2, 3)$ |
Means of Intercepts | $\mu _{\eta _{0}}=(98, 102), (d=0.86)$ | $\mu _{\eta _{0}}=(96, 100, 104)$ |
| $\mu _{\eta _{0}}=(96, 104), (d=1.72)$ |
|
Scenario 2: Different means of slope 1 and (means of) knot locations
| ||
Variables | 2 latent classes | 3 latent classes |
Means of Intercepts | $\mu _{\eta _{0}}^{(k)}=100$ $(k=1,2)$ | $\mu _{\eta _{0}}^{(k)}=100$ $(k=1,2,3)$ |
Means of Slope 2’s | $\mu _{\eta _{2}}^{(k)}=-2$ $(k=1, 2)$ | $\mu _{\eta _{2}}^{(k)}=-2$ $(k=1, 2, 3)$ |
Means of Slope 1’s | $\mu _{\eta _{1}}=(-4.4, -3.6), (d=0.86)$ | $\mu _{\eta _{1}}=(-5.2, -4.4, -3.6)$ |
| $\mu _{\eta _{1}}=(-5.2, -3.6), (d=1.72)$ |
|
Scenario 3: Different means of slope 2 and (means of) knot locations
| ||
Variables | 2 latent classes | 3 latent classes |
Means of Intercepts | $\mu _{\eta _{0}}^{(k)}=100$ $(k=1,2)$ | $\mu _{\eta _{0}}^{(k)}=100$ $(k=1,2,3)$ |
Means of Slope 1’s | $\mu _{\eta _{1}}^{(k)}=-5$ $(k=1,2)$ | $\mu _{\eta _{1}}^{(k)}=-5$ $(k=1, 2, 3)$ |
Means of Slope 2’s | $\mu _{\eta _{2}}=(-2.6, -3.4), (d=0.86)$ | $\mu _{\eta _{2}}=(-1.8, -2.6, -3.4)$ |
| $\mu _{\eta _{2}}=(-1.8, -3.4), (d=1.72)$ |
|
For both parts, the primary aim was to investigate how the separation between latent classes, the unbalanced class mixing proportion, and the trajectory shape affected the model performance. Utilizing a model-based clustering algorithm, we are usually interested in examining how well the model can detect heterogeneity in samples and estimate parameters of interest in each latent class. Intuitively, the model should perform better under those conditions with a larger separation between latent classes. We wanted to test this hypothesis. In the simulation design, we had two metrics to gauge the separation between clusters: the difference between the knot locations and the Mahalanobis distance (MD) of the three growth factors of latent classes. We set $1$, $1.5$ and $2$ as a small, medium, and large difference between the knot locations. We chose $1$ as the level of small difference to follow the rationale in Kohli et al. (2015) and considered the other two levels to investigate whether the more widely spaced knots improve the model performance. We considered two levels of MD, $0.86$ (i.e., small distance) and $1.72$ (i.e., large distance), for class separation. Note that both the small and large distance in the current simulation design was smaller than the corresponding level in Kohli et al. (2015) because we wanted to examine the proposed model under more challenging conditions in terms of cluster separation.
We chose two levels of mixing proportion, 1:1 and 1:2, for the conditions with two latent classes and three levels of mixing proportion, 1:1:1, 1:1:2 and 1:2:2, for the scenarios with three clusters. We selected these levels because we wanted to evaluate how the challenging conditions (i.e., the unbalanced allocation) affect performance measures and clustering effects. We also examined several common change patterns shown in Table 2 (Scenario 1, 2 and 3). We changed the knot locations and one growth factor under each scenario but fixed the other two growth factors to satisfy the specified MD. We considered $\theta =1$ or $\theta =2$ as two levels of homogeneous residual variances across latent classes to see the effect of the measurement precision, and we considered two levels of sample size.
All mixture models suffer from the label switching issue: inconsistent assignments of membership for multiple replications in simulation studies. The label switching does not hurt the model estimation in the frequentist framework since the likelihood is invariant to permutation of cluster labels; however, the estimates from the first latent class may be mislabeled as such from other latent classes (Class 2 or Class 3 in our case) (Tueller, Drotar, & Lubke, 2011). In this study, we utilized the column maxima switched label detection algorithm developed by Tueller et al. (2011) to check whether the labels were switched; and if it occurred, the final estimates were relabeled in the correct order before model evaluation.
For each condition listed in Table 2, we used two-step data generation to obtain a component label $z_{i}$ for each individual and then generated data for each component. The general steps of the simulation for the proposed two-step model in the framework of individual measurement occasions were carried out as follows:
In this section, we first examine the convergence4 rate of two steps for each condition. Based on our simulation studies, the convergence rate of the proposed two-step model achieved around $90\%$ for all conditions, and the majority of non-convergence cases occurred in the first step. To elaborate, for the conditions with two latent classes, $96$ out of total $288$ conditions reported $100\%$ convergence rate, while for the conditions with three latent classes, $12$ out of total $144$ conditions reported $100\%$ convergence rate. Among all conditions with two latent classes, the worst scenario regarding the convergence rate was $121/1121$, indicating that we need to replicate the procedure described in Section 3.3 $1,121$ times to have $1,000$ replications with a convergent solution. Across all scenarios with three latent classes, the worst condition was $134/1134$5.
In this section, we evaluate the performance measures of the proposed model across the conditions with fixed knots (i.e., knots without considering variability), under which the proposed model was specified correctly. In the result section, we named the latent classes from left to right as Class 1 (the left cluster) and Class 2 (the right cluster) and called them as Class 1 (the left cluster), Class 2 (the middle cluster) and Class 3 (the right cluster) for the model with two and three pre-specified clusters, respectively. We first calculated each performance metric across $1,000$ replications for each parameter of interest under each condition with two latent classes and fixed knots. We then summarized each metric across all conditions as the corresponding median and range.
Tables 3 and 4 present the median (range) of the relative bias and empirical SE for each parameter of interest of the two-step model, respectively. We observed that the proposed model generated unbiased point estimates with small empirical SEs when being specified correctly in the first step. Specifically, the magnitude of the relative biases of the growth factor means and growth factor variances across all conditions were under $0.016$ and $0.038$, respectively. In the second step, the median of relative bias of the logistic coefficients was around $-0.010$, although they may be underestimated under conditions with the small sample size (i.e., $n=500$), the small difference in knot locations (i.e., the difference is $1$) and less precise measurements (i.e., $\theta _{\epsilon }=2$). From Table 4, the magnitude of empirical SE of all parameters except intercept means and variances were under $0.52$ (i.e., the variances of estimates were under $0.25$), though the median value of empirical SE of $\mu _{\eta _{0}}$ and $\psi _{00}$ were around $0.40$ and $2.50$, respectively.
| Parameters | Latent Class $1$ | Latent Class $2$ | |
Mean | $\mu _{\eta _{0}}$ | $0.000$ ($0.000$, $0.001$) | $0.000$ ($-0.001$, $0.000$) |
| $\mu _{\eta _{1}}$ | $0.000$ ($-0.008$, $0.003$) | $0.001$ ($-0.001$, $0.012$) | |
| $\mu _{\eta _{2}}$ | $0.000$ ($-0.009$, $0.016$) | $-0.002$ ($-0.012$, $0.003$) | |
| $\mu _{\gamma }$ | $0.000$ ($-0.001$, $0.002$) | $0.000$ ($-0.001$, $0.002$) | |
Variance | $\psi _{00}$ | $-0.002$ ($-0.014$, $0.006$) | $-0.005$ ($-0.031$, $0.005$) |
| $\psi _{11}$ | $-0.005$ ($-0.028$, $0.028$) | $-0.007$ ($-0.038$, $0.003$) | |
| $\psi _{22}$ | $-0.005$ ($-0.026$, $0.031$) | $-0.007$ ($-0.037$, $0.005$) | |
Path Coef. | $\beta _{0}$ | — | $-0.009$ (NA, NA) |
| $\beta _{1}$ | — | $-0.012$ ($-0.225$, $0.018$) | |
| $\beta _{2}$ | — | $-0.010$ ($-0.218$, $0.015$) | |
NA: Note that for the conditions with balanced allocation, the population value of $\beta _{0}=0$ and its relative bias goes infinity. The bias median (range) of $\beta _{0}$ is $-0.002$ ($-0.070$, $0.017$).
| Parameters | Latent Class $1$ | Latent Class $2$ | |
Mean | $\mu _{\eta _{0}}$ | $0.422$ ($0.242$, $0.933$) | $0.336$ ($0.198$, $0.709$) |
| $\mu _{\eta _{1}}$ | $0.101$ ($0.051$, $0.276$) | $0.073$ ($0.042$, $0.175$) | |
| $\mu _{\eta _{2}}$ | $0.100$ ($0.054$, $0.276$) | $0.072$ ($0.042$, $0.160$) | |
| $\mu _{\gamma }$ | $0.039$ ($0.017$, $0.110$) | $0.046$ ($0.020$, $0.134$) | |
Variance | $\psi _{00}$ | $2.662$ ($1.692$, $5.073$) | $2.173$ ($1.423$, $3.942$) |
| $\psi _{11}$ | $0.124$ ($0.073$, $0.296$) | $0.093$ ($0.059$, $0.168$) | |
| $\psi _{22}$ | $0.126$ ($0.072$, $0.286$) | $0.095$ ($0.062$, $0.178$) | |
Path Coef. | $\beta _{0}$ | — | $0.168$ ($0.083$, $0.516$) |
| $\beta _{1}$ | — | $0.120$ ($0.080$, $0.200$) | |
| $\beta _{2}$ | — | $0.124$ ($0.082$, $0.198$) | |
Table 5 list the median (range) of relative RMSE of each parameter, which assesses the point estimates holistically. From the table, the model was capable of estimating the parameters accurately in the first step. Under the conditions with two latent classes and fixed knots, the magnitude of the relative RMSEs of the growth factor means and variances were under $0.081$ and $0.296$, respectively. The relative RMSE of the logistic coefficients was relatively larger under some conditions due to their larger relative biases.
| Para. | Latent Class $1$ | Latent Class $2$ | |
Mean | $\mu _{\eta _{0}}$ | $0.004$ ($0.002$, $0.009$) | $0.003$ ($0.002$, $0.007$) |
| $\mu _{\eta _{1}}$ | $-0.021$ ($-0.063$, $-0.010$) | $-0.016$ ($-0.045$, $-0.009$) | |
| $\mu _{\eta _{2}}$ | $-0.045$ ($-0.112$, $-0.020$) | $-0.028$ ($-0.081$, $-0.012$) | |
| $\mu _{\gamma }$ | $0.010$ ($0.005$, $0.028$) | $0.009$ ($0.004$, $0.027$) | |
Variance | $\psi _{00}$ | $0.106$ ($0.068$, $0.203$) | $0.087$ ($0.057$, $0.161$) |
| $\psi _{11}$ | $0.124$ ($0.074$, $0.296$) | $0.093$ ($0.060$, $0.172$) | |
| $\psi _{22}$ | $0.126$ ($0.072$, $0.288$) | $0.095$ ($0.062$, $0.182$) | |
Path Coef. | $\beta _{0}$ | — | NA ($0.121$, NA) |
| $\beta _{1}$ | — | $0.297$ ($0.197$, $0.542$) | |
| $\beta _{2}$ | — | $0.234$ ($0.155$, $0.431$) | |
Table 6 shows the median (range) of the coverage probability for each parameter of interest of the two-step model with two latent classes under conditions with fixed knots. Overall, the proposed model performed well regarding empirical coverage under the conditions with the relatively large separation between two latent classes and the higher measurement precision. Specifically, coverage probability of all parameters except knots and intercept coefficient $\beta _{0}$ can achieve at least $90\%$ across all conditions with a medium or large separation between the knot locations (i.e., $1.5$ or $2$) and small residual variance (i.e., $\theta _{\epsilon }=1$).
| Small Separation between the Knots Locations
| |||||
| Latent Class $1$ | Latent Class $2$ | ||||
| Small Residuals | Large Residuals | Small Residuals | Large Residuals | ||
| $\mu _{\eta _{0}}$ | $.937$ ($.913$, $.961$) | $.915$ ($.866$, $.950$) | $.942$ ($.920$, $.971$) | $.919$ ($.867$, $.952$) | |
| $\mu _{\eta _{1}}$ | $.919$ ($.861$, $.948$) | $.874$ ($.766$, $.942$) | $.936$ ($.901$, $.962$) | $.904$ ($.819$, $.941$) | |
| $\mu _{\eta _{2}}$ | $.926$ ($.849$, $.949$) | $.893$ ($.747$, $.940$) | $.938$ ($.888$, $.956$) | $.913$ ($.855$, $.949$) | |
| $\mu _{\gamma }$ | $.629$ ($.493$, $.724$) | $.476$ ($.290$, $.623$) | $.522$ ($.406$, $.685$) | $.355$ ($.227$, $.541$) | |
| $\psi _{00}$ | $.939$ ($.916$, $.954$) | $.932$ ($.896$, $.950$) | $.939$ ($.927$, $.957$) | $.925$ ($.888$, $.963$) | |
| $\psi _{11}$ | $.933$ ($.878$, $.950$) | $.921$ ($.831$, $.957$) | $.935$ ($.911$, $.966$) | $.927$ ($.877$, $.947$) | |
| $\psi _{22}$ | $.929$ ($.862$, $.950$) | $.904$ ($.809$, $.935$) | $.938$ ($.902$, $.961$) | $.930$ ($.888$, $.957$) | |
| $\beta _{0}$ | — | — | $.789$ ($.665$, $.854$) | $.643$ ($.502$, $.739$) | |
| $\beta _{1}$ | — | — | $.950$ ($.935$, $.960$) | $.936$ ($.891$, $.957$) | |
| $\beta _{2}$ | — | — | $.944$ ($.930$, $.959$) | $.933$ ($.873$, $.958$) | |
| Medium Separation between the Knots Locations
| |||||
| Latent Class $1$ | Latent Class $2$ | ||||
| Small Residuals | Large Residuals | Small Residuals | Large Residuals | ||
| $\mu _{\eta _{0}}$ | $.944$ ($.918$, $.959$) | $.929$ ($.899$, $.951$) | $.943$ ($.923$, $.957$) | $.932$ ($.905$, $.955$) | |
| $\mu _{\eta _{1}}$ | $.938$ ($.897$, $.957$) | $.922$ ($.833$, $.951$) | $.947$ ($.917$, $.959$) | $.932$ ($.884$, $.959$) | |
| $\mu _{\eta _{2}}$ | $.935$ ($.910$, $.948$) | $.913$ ($.835$, $.947$) | $.940$ ($.913$, $.959$) | $.934$ ($.883$, $.954$) | |
| $\mu _{\gamma }$ | $.814$ ($.786$, $.854$) | $.740$ ($.684$, $.800$) | $.767$ ($.721$, $.833$) | $.682$ ($.626$, $.780$) | |
| $\psi _{00}$ | $.940$ ($.925$, $.953$) | $.935$ ($.912$, $.955$) | $.944$ ($.927$, $.953$) | $.939$ ($.901$, $.950$) | |
| $\psi _{11}$ | $.939$ ($.905$, $.952$) | $.929$ ($.853$, $.953$) | $.939$ ($.914$, $.961$) | $.937$ ($.909$, $.952$) | |
| $\psi _{22}$ | $.930$ ($.906$, $.958$) | $.920$ ($.878$, $.951$) | $.939$ ($.917$, $.962$) | $.934$ ($.889$, $.951$) | |
| $\beta _{0}$ | — | — | $.858$ ($.782$, $.905$) | $.770$ ($.658$, $.839$) | |
| $\beta _{1}$ | — | — | $.954$ ($.937$, $.961$) | $.944$ ($.921$, $.965$) | |
| $\beta _{2}$ | — | — | $.949$ ($.934$, $.964$) | $.942$ ($.923$, $.961$) | |
| Large Separation between the Knots Locations
| |||||
| Latent Class $1$ | Latent Class $2$
| ||||
| Small Residuals | Large Residuals | Small Residuals | Large Residuals | ||
| $\mu _{\eta _{0}}$ | $.946$ ($.931$, $.955$) | $.938$ ($.921$, $.965$) | $.946$ ($.932$, $.959$) | $.940$ ($.921$, $.967$) | |
| $\mu _{\eta _{1}}$ | $.938$ ($.921$, $.959$) | $.936$ ($.875$, $.953$) | $.947$ ($.926$, $.958$) | $.937$ ($.893$, $.961$) | |
| $\mu _{\eta _{2}}$ | $.939$ ($.907$, $.956$) | $.928$ ($.876$, $.951$) | $.949$ ($.937$, $.964$) | $.940$ ($.916$, $.955$) | |
| $\mu _{\gamma }$ | $.952$ ($.935$, $.970$) | $.946$ ($.935$, $.961$) | $.950$ ($.933$, $.965$) | $.946$ ($.932$, $.960$) | |
| $\psi _{00}$ | $.946$ ($.929$, $.957$) | $.944$ ($.916$, $.963$) | $.943$ ($.916$, $.958$) | $.942$ ($.921$, $.959$) | |
| $\psi _{11}$ | $.938$ ($.917$, $.952$) | $.934$ ($.859$, $.951$) | $.942$ ($.918$, $.955$) | $.938$ ($.902$, $.956$) | |
| $\psi _{22}$ | $.935$ ($.910$, $.950$) | $.928$ ($.857$, $.951$) | $.946$ ($.925$, $.959$) | $.938$ ($.919$, $.953$) | |
| $\beta _{0}$ | — | — | $.892$ ($.825$, $.924$) | $.805$ ($.703$, $.865$) | |
| $\beta _{1}$ | — | — | $.950$ ($.927$, $.958$) | $.949$ ($.937$, $.960$) | |
| $\beta _{2}$ | — | — | $.950$ ($.934$, $.964$) | $.946$ ($.924$, $.958$) | |
Additionally, when being specified correctly, the model with three latent classes, similar to that with two clusters, performed well in terms of performance measures, though we noticed that the empirical SE of parameters in the middle cluster were slightly larger than those in the other two groups.
In this section, we assess the robustness of the proposed model by examining the performance measures in the presence of random knots (i.e., the knots with the standard deviation set as $0.3$), under which the model was underspecified. We noted that the relative biases increased slightly and that the empirical SE did not change meaningfully when the proposed model was misspecified, which decreased the performance of relative RMSE and coverage probability. For those conditions under which the model was underspecified, the summary of the relative bias and empirical SE were provided in 6.2.
In this section, we evaluate the clustering effects across all conditions that we considered in the simulation design. We first calculated mean values of accuracy and entropy across $1,000$ Monte Carlo replications for each condition. Of all the conditions we investigated, the mean entropy ranges from $0.3$ to $0.8$, while the mean accuracy ranges from $0.55$ to $0.95$. Factors such as the separation between two latent classes and the precision of measurements were the primary determinants of entropy and accuracy.
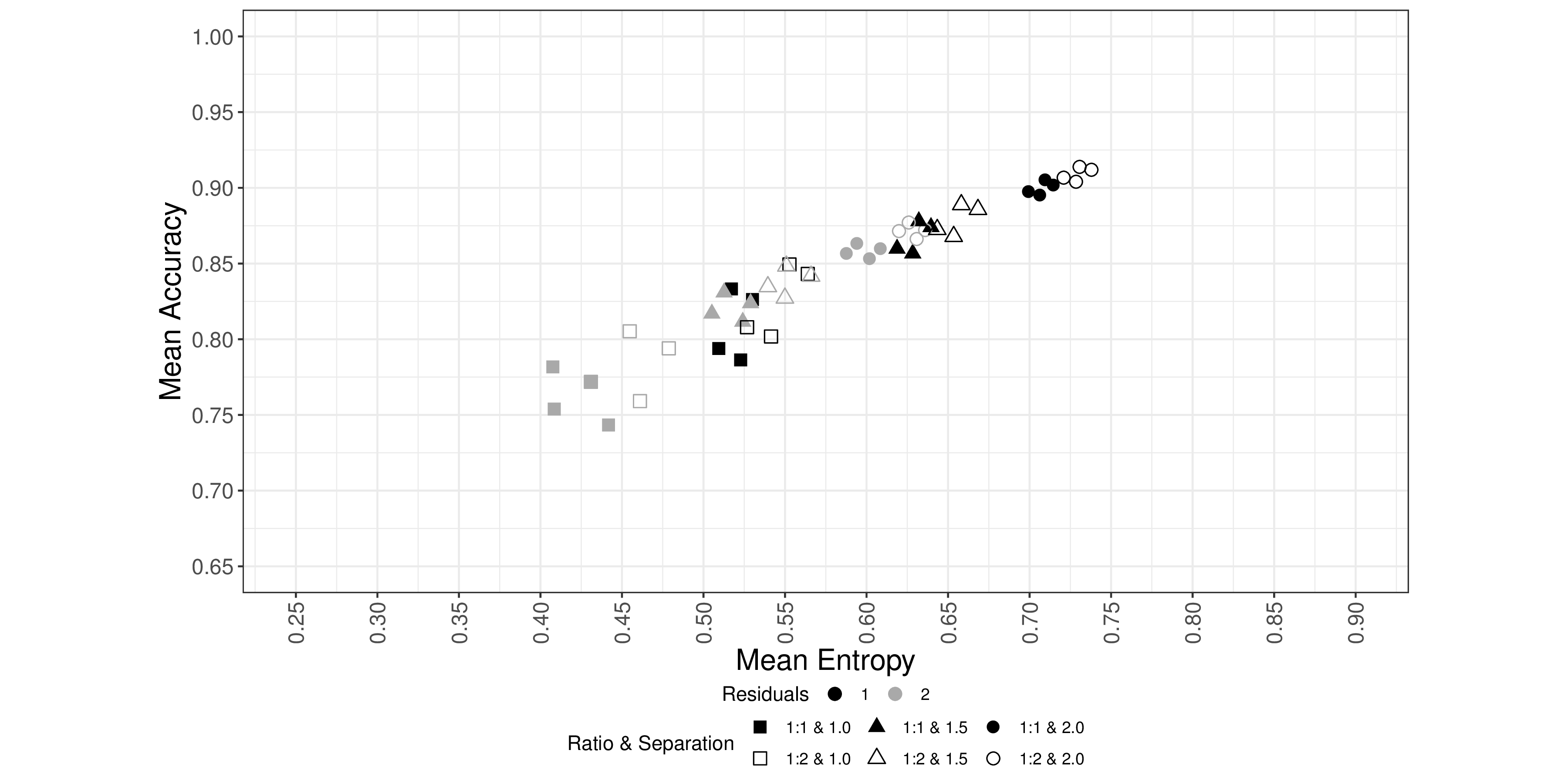
Figure 1 depicts the mean accuracy against the mean entropy for each condition with two latent classes, the small Mahalanobis distance, and change patterns of Scenario $1$ listed in Table 2. In the plot, we colored the conditions with the smaller and the larger residual variances black and grey, respectively. Squares, triangles, and circles are for the small, medium, and large differences between the locations of the knots. Additionally, we set solid and hollow shapes for the proportions 1:1 and 1:2, respectively. From the figure, we observed that both entropy and accuracy increased when the separation between two latent classes increased and as the residual variances were small. Additionally, unbalanced allocation tended to yield relatively larger accuracy and entropy. We also noticed that the scenario of change patterns only affected entropy and accuracy slightly, while other factors such as the knot standard deviation and the sample size did not have meaningful impacts on entropy and accuracy. We observed the same patterns between the mean accuracy and the mean entropy of conditions with three latent classes.
In this section, we demonstrate how to fit the proposed model to separate nonlinear trajectories and associate the ‘soft clusters’ to the baseline characteristics using the motivating data. We extracted a random subsample ($n=500$) from the Early Childhood Longitudinal Study Kindergarten Cohort: 2010-11 (ECLS-K: 2011) with complete records of repeated mathematics IRT scaled scores, demographic information (sex, race, and age in months at each wave), baseline school information (school location and baseline school type), baseline social-economic status (family income and the highest education level between parents), baseline teacher-reported social skills (including interpersonal skills, self-control ability, internalizing problem, externalizing problem), baseline teacher-reported approach to learning, and baseline teacher-reported children behavior question (including inhibitory control and attentional focus)6.
ECLS-K: 2011 is a nationally representative longitudinal sample of US children enrolled in about $900$ kindergarten programs beginning with $2010-2011$ school year, where children’s mathematics ability was evaluated in nine waves: fall and spring of kindergarten ($2010-2011$), first ($2011-2012$) and second ($2012-2013$) grade, respectively as well as spring of $3^{rd}$ ($2014$), $4^{th}$ ($2015$) and $5^{th}$ ($2016$), respectively. Only about $30\%$ students were assessed in the fall of $2011$ and $2012$ (Lê, Norman, Tourangeau, Brick, & Mulligan, 2011). In the analysis, we used children’s age (in months) rather than their grade-in-school to obtain the time structure with individual measurement occasions. In the subset data, $52\%$ of students were boys, and $48\%$ of students were girls. Additionally, $50\%$ of students were White, $4.8\%$ were Black, $30.4\%$ were Hispanic, $0.2\%$ were Asian, and $14.6\%$ were others. We dichotomized the variable race to be White ($50\%$) and others ($50\%$) for this analysis. At the beginning of the study, $87\%$ and $13\%$ students were from public and private schools, respectively. The covariates including school location (ranged between $1$ and $4$), family income (ranged between $1$ and $18$) and the highest parents’ education (ranged between $0$ and $8$) were treated as a continuous variables, and the corresponding mean (SD) was $2.11$ ($1.12$), $11.99$ ($5.34$) and $5.32$ ($1.97$), respectively.
In the first step, we first fit a latent growth curve model with a linear-linear piecewise functional form and three GMMs with two-, three- and four-class and provided the obtained estimated likelihood, information criteria (AIC and BIC), residual of each latent class in Table 7. All four models converged. As introduced earlier, the BIC is a compelling information criterion for the enumeration process as it penalizes model complexity and adjusts for sample size (Nylund et al., 2007). The four fits led to BIC values of $31728.23$, $31531.60$, $31448.99$, and $31478.35$, respectively, which led to the selection of the GMM with three latent classes.
| $1$-Class | $2$-Class | $3$-Class | $4$-Class | |
| -2LL | 31659.87 | 31388.67 | 31231.48 | 31186.26 |
| AIC | 31681.87 | 31434.67 | 31301.48 | 31280.26 |
| BIC | 31728.23 | 31531.6 | 31448.99 | 31478.35 |
| Residual 1 | 35.6 | 28.57 | 28.47 | 26.78 |
| Residual 2 | - | 35.02 | 33.89 | 32.51 |
| Residual 3 | - | - | 32.03 | 33.36 |
| Residual 4 | - | - | - | 26.63 |
Table 8 presents the estimates of growth factors from which we obtained the model implied trajectory of each latent group, as shown in Figure 2. The estimated proportions in Class $1$, $2$ and $3$ were $29.6\%$, $47.8\%$ and $22.6\%$, respectively. On average, students in Class $1$ had the lowest levels of mathematics achievement throughout the entire duration (the fixed effects of the baseline and two slopes were $24.133$, $1.718$ per month, and $0.841$ per month, respectively). On average, students in Class $2$ had a similar initial score and slope for the first stage but relatively lower slope in the second stage (the fixed effects of the baseline and two slopes were $24.498$, $1.730$ per month, and $0.588$ per month, respectively) compared to the students in the Class $1$. Students in Class $3$ had the best mathematics performance on average (the fixed effects of the baseline and two slopes were $36.053$, $2.123$ per month, and $0.605$ per month, respectively). For all three classes, post-knot development in mathematics skills slowed substantially, yet the change to the slower growth rate occurred earlier for Class $1$ and $3$ (around $8$-year old: $91$ and $97$ months, respectively) than Class $2$ (around $9$-year old, $110$ months). Additionally, for each latent class, the estimates of the intercept variance and first slope variance were statistically significant, indicating that each student had a ‘personal’ intercept and pre-knot slope, and then a ‘personal’ trajectory of the development in mathematics achievement.
| Estimate (SE) | P value | |||
Class 1 |
Mean | Intercept$^{1}$ | $24.133$ ($1.250$) | $<0.0001^{\ast }$ |
| Slope $1$ | $1.718$ ($0.052$) | $<0.0001^{\ast }$ | ||
| Slope $2$ | $0.841$ ($0.031$) | $<0.0001^{\ast }$ | ||
| Knot | $90.788$ ($0.733$) | $<0.0001^{\ast }$ | ||
Variance | Intercept | $79.696$ ($17.419$) | $<0.0001^{\ast }$ | |
| Slope $1$ | $0.104$ ($0.023$) | $<0.0001^{\ast }$ | ||
| Slope $2$ | $0.049$ ($0.011$) | $<0.0001^{\ast }$ | ||
Class 2 |
Mean | Intercept$^{1}$ | $24.498$ ($0.813$) | $<0.0001^{\ast }$ |
| Slope $1$ | $1.730$ ($0.024$) | $<0.0001^{\ast }$ | ||
| Slope $2$ | $0.588$ ($0.032$) | $<0.0001^{\ast }$ | ||
| Knot | $109.653$ ($0.634$) | $<0.0001^{\ast }$ | ||
Variance | Intercept | $77.302$ ($11.973$) | $<0.0001^{\ast }$ | |
| Slope $1$ | $0.026$ ($0.007$) | $0.0002^{\ast }$ | ||
| Slope $2$ | $0.012$ ($0.011$) | $0.2753$ | ||
Class 3 |
Mean | Intercept$^{1}$ | $36.053$ ($1.729$) | $<0.0001^{\ast }$ |
| Slope $1$ | $2.123$ ($0.035$) | $<0.0001^{\ast }$ | ||
| Slope $2$ | $0.605$ ($0.027$) | $<0.0001^{\ast }$ | ||
| Knot | $97.610$ ($0.068$) | $<0.0001^{\ast }$ | ||
| Variance | Intercept | $211.198$ ($36.057$) | $<0.0001^{\ast }$ | |
| Slope $1$ | $0.065$ ($0.017$) | $0.0001^{\ast }$ | ||
| Slope $2$ | $-0.002$ ($0.006$) | $0.7389$ | ||

Table 9 summarizes the estimates of the second step of the GMM to associate ‘soft clusters’ of mathematics achievement trajectories to individual-level covariates. From the table, we noticed that the impacts of some covariates, such as baseline socioeconomic status and teacher-reported skills, may differ with or without other covariates. For example, higher family income, higher parents’ education, higher-rated attentional focus, and inhibitory control increased the likelihood of being in Class $2$ or Class $3$ in univariable analyses, while these four baseline characteristics only associated with Class $3$ in multivariable analyses. It is reasonable that the effect sizes of the Class $3$ were larger than those of the Class $2$, given its more evident difference from the reference group, as shown in Table 8 and Figure 2. However, it is still too rush to neglect that students from families with higher socioeconomic status and/or higher-rated behavior questions were more likely to be in Class $2$ at the significant level of $0.05$ in an exploratory study. Another possible explanation for this phenomenon is multicollinearity.
| Class $2$ | |||
Predictor | Uni-variable | Multi-variable
| ||
| OR | $95\%$ CI | OR | $95\%$ CI |
Sex($0-$Boy; $1-$Girl) | $0.435$ | ($0.254$, $0.745$)$^{\ast }$ | $0.332$ | ($0.174$, $0.633$)$^{\ast }$ |
Race($0-$White; $1-$Other) | $0.764$ | ($0.455$, $1.281$) | $1.249$ | ($0.624$, $2.498$) |
School Location | $1.407$ | ($1.093$, $1.811$)$^{\ast }$ | $1.357$ | ($0.981$, $1.877$) |
Parents’ Highest Education | $1.208$ | ($1.051$, $1.388$)$^{\ast }$ | $1.155$ | ($0.933$, $1.431$) |
Income | $1.074$ | ($1.023$, $1.128$)$^{\ast }$ | $1.067$ | ($0.987$, $1.154$) |
School Type ($0-$Public; $1-$Private) | $0.573$ | ($0.250$, $1.317$) | $0.442$ | ($0.149$, $1.313$) |
Approach to Learning | $1.305$ | ($0.883$, $1.929$) | $0.957$ | ($0.384$, $2.389$) |
Self-control | $1.146$ | ($0.764$, $1.718$) | $0.663$ | ($0.272$, $1.616$) |
Interpersonal Skills | $1.479$ | ($0.959$, $2.282$) | $1.276$ | ($0.513$, $3.175$) |
External Prob Behavior | $0.858$ | ($0.559$, $1.319$) | $1.391$ | ($0.571$, $3.386$) |
Internal Prob Behavior | $1.139$ | ($0.658$, $1.972$) | $1.190$ | ($0.589$, $2.406$) |
Attentional Focus | $1.251$ | ($1.035$, $1.511$)$^{\ast }$ | $1.139$ | ($0.764$, $1.698$) |
Inhibitory Control | $1.238$ | ($1.007$, $1.520$)$^{\ast }$ | $1.557$ | ($0.915$, $2.649$) |
| Class $3$
| |||
Predictor | Uni-variable | Multi-variable
| ||
| OR | $95\%$ CI | OR | $95\%$ CI |
Sex($0-$Boy; $1-$Girl) | $0.379$ | ($0.205$, $0.700$)$^{\ast }$ | $0.212$ | ($0.098$, $0.459$)$^{\ast }$ |
Race($0-$White; $1-$Other) | $0.397$ | ($0.219$, $0.721$)$^{\ast }$ | $0.943$ | ($0.429$, $2.073$) |
School Location | $1.266$ | ($0.957$, $1.676$) | $1.211$ | ($0.835$, $1.755$) |
Parents’ Highest Education | $1.713$ | ($1.418$, $2.068$)$^{\ast }$ | $1.345$ | ($1.043$, $1.734$)$^{\ast }$ |
Income | $1.241$ | ($1.155$, $1.334$)$^{\ast }$ | $1.195$ | ($1.083$, $1.318$)$^{\ast }$ |
School Type ($0-$Public; $1-$Private) | $1.437$ | ($0.661$, $3.124$) | $0.665$ | ($0.234$, $1.892$) |
Approach to Learning | $2.624$ | ($1.590$, $4.332$)$^{\ast }$ | $5.363$ | ($1.731$, $16.612$)$^{\ast }$ |
Self-control | $1.436$ | ($0.903$, $2.284$) | $0.414$ | ($0.136$, $1.265$) |
Interpersonal Skills | $1.740$ | ($1.057$, $2.862$)$^{\ast }$ | $0.771$ | ($0.269$, $2.209$) |
External Prob Behavior | $0.761$ | ($0.451$, $1.283$) | $1.565$ | ($0.561$, $4.367$) |
Internal Prob Behavior | $0.787$ | ($0.405$, $1.532$) | $1.170$ | ($0.488$, $2.808$) |
Attentional Focus | $1.601$ | ($1.253$, $2.045$)$^{\ast }$ | $1.095$ | ($0.671$, $1.787$)$^{\ast }$ |
Inhibitory Control | $1.439$ | ($1.116$, $1.855$)$^{\ast }$ | $1.324$ | ($0.720$, $2.434$)$^{\ast }$ |
Figure 3 visualizes the correlation matrix of all baseline characteristics, from which we can see that two socioeconomic variables, family income and parents’ highest education, were highly correlated ($\rho =0.66$). Additionally, teacher-rated baseline abilities were highly correlated; for example, the correlation of approach to learning with self-control, interpersonal ability, attentional focus, and inhibitory control was $0.68$, $0.72$, $0.79$ and $0.79$, respectively. We then conducted the exploratory factor analysis to address this collinearity issue for socioeconomic variables and teacher-reported abilities.
The exploratory factor analysis was conducted using the R function factanal in the stats package (R Core Team, 2020) with $2$ specified factors as suggested by the eigenvalues greater than $1$ (EVG$1$) component retention criterion, scree test (Cattell, 1966; Cattell & Jaspers, 1967), and parallel analysis (Horn, 1965; Humphreys & Ilgen, 1969; Humphreys & Montanelli, 1975). We employed the ‘varimax’ option to get a type of orthogonal rotation (Kaiser, 1958). By using Bartlett’s weighted least-squares methods, we obtained the factor scores. Table 10 summarizes the results from the EFA. The first factor differentiates between teacher-rated abilities and teacher-reported problems; the second factor can be interpreted as general socioeconomic status. We then re-ran the second step with the two factors as well as demographic information and school information.
| Factor Loadings
| ||
| Baseline Characteristics | Factor 1 | Factor 2 |
| Parents’ Highest Education | $0.10$ | $0.76$ |
| Family Income | $0.03$ | $0.86$ |
| Approach to Learning | $0.90$ | $0.04$ |
| Self-control | $0.77$ | $0.08$ |
| Interpersonal Skills | $0.76$ | $0.05$ |
| External Prob Behavior | $-0.72$ | $0.00$ |
| Internal Prob Behavior | $-0.24$ | $-0.07$ |
| Attentional Focus | $0.83$ | $0.07$ |
| Inhibitory Control | $0.89$ | $0.01$ |
| Explained Variance
| ||
| Factor 1 | Factor 2 | |
| SS Loadings | $4.04$ | $1.34$ |
| Proportion Variance | $0.45$ | $0.15$ |
| Cumulative Variance | $0.45$ | $0.60$ |
Table 11 summarizes the estimates obtained from the second step with factor scores, demographic information, and school information. From the table, we observed that boys with higher values of the first factor scores, and higher values of the second factor scores were more likely to be in Class $2$7 or Class $3$8. It suggests that both socioeconomic variables and teacher-rated abilities were positively associated with mathematics performance, while externalizing/internalizing problems were negative associated with mathematics achievement.
Predictor | Class $2$ | Class $3$ | ||
| OR | $95\%$ CI | OR | $95\%$ CI |
Sex($0-$Boy; $1-$Girl) | $0.345$ | ($0.183$, $0.651$)$^{\ast }$ | $0.234$ | ($0.111$, $0.494$)$^{\ast }$ |
Race($0-$White; $1-$Other) | $1.221$ | ($0.638$, $2.339$) | $1.021$ | ($0.486$, $2.145$) |
School Type ($0-$Public; $1-$Private) | $0.439$ | ($0.149$, $1.291$) | $0.709$ | ($0.244$, $2.056$) |
School Location | $1.333$ | ($0.995$, $1.786$) | $1.133$ | ($0.806$, $1.593$) |
Factor $1$ | $1.454$ | ($1.090$, $1.939$)$^{\ast }$ | $2.006$ | ($1.408$, $2.858$)$^{\ast }$ |
Factor $2$ | $1.656$ | ($1.226$, $2.235$)$^{\ast }$ | $3.410$ | ($2.258$, $5.148$)$^{\ast }$ |
This article extends Bakk and Kuha (2017) study to conduct a stepwise analysis to investigate the heterogeneity in nonlinear trajectories. We fit a growth mixture model with a bilinear spline functional form to describe the underlying change pattern of nonlinear trajectories in the first step. In the second step, we investigated the associations between the ‘soft’ clusters and baseline characteristics. Although this stepwise method follows the recommended approach to fit a FMM model (i.e., separate the estimation of the class-specific parameters and that of the logistic coefficients), it is not our aim to show that this stepwise approach is universally preferred. Based on our understanding, this approach is more suitable for an exploratory study where empirical researchers only have vague assumptions in terms of sample heterogeneity and its possible causes.
On the one hand, the two-step model can save computational budget as we only need to refit the second-step model rather than the whole model when adding or removing covariates. On the other hand, our simulation study showed that the proposed model works well in terms of performance measures and accuracy, especially under preferable conditions, such as well-separated latent classes and precise measurements. This stepwise approach can also be utilized to analyze any other types of FMMs in the SEM framework to explore sample heterogeneity.
Although this stepwise model can expedite the exploratory process, it is still challenging to decide which covariates should be added in the mixture model to inform the class formation. An additional challenge lies in that, in the psychological and behavioral research where the SEM framework is widely used, the candidate pool of covariates is huge, or some variables are highly correlated (i.e., collinearity issue), as shown in the application.
In the statistical and machine learning (ML) literature, multiple approaches have been proposed to reduce the number of covariates. These methods include greedy search, regularization to select covariates based on their corresponding coefficients, principal component analysis (PCA) to transform all features to space with fewer dimensions, and tree-based models (such as regression and classification trees, boosting, and bagging). In the SEM framework, the majority of counterparts of the above models have been proposed. For example, Marcoulides and Drezner (2003); Marcoulides, Drezner, and Schumacker (1998) proposed to conduct a heuristic specification search algorithm to identify an optimal set of models; Jacobucci, Grimm, and McArdle (2016); Scharf and Nestler (2019); Sun, Chen, Liu, Ying, and Xin (2016), demonstrated how to regularize parameters in the SEM framework to reduce the complexity of the model by selecting or removing paths (i.e., variables). Additionally, by applying a tree-based model Brandmaier, von Oertzen, McArdle, and Lindenberger (2013), Jacobucci, Grimm, and McArdle (2017) captured the heterogeneity in trajectories with respect to baseline covariates, where the FMM was compared with the tree-based model in terms of membership components and result interpretation.
This article proposes to employ the EFA to reduce the dimensions of covariates and address the multicollinearity issue. In this application, we applied the EFA in a process termed as ‘feature engineering’ in the ML literature, where researchers employ the PCA technique to reduce the covariate space and address the multicollinearity issue conventionally, as the interpretation of covariate coefficients is out of the primary interest in the ML literature. In this article, we decided to use the EFA rather than the PCA for two reasons. First, empirical researchers using the SEM framework are more familiar with the EFA as the idea behind it is very similar to another model in the SEM framework, the confirmatory factor analysis (CFA). More importantly, the factors (i.e., latent variables) obtained from the EFA are interpretable so that the estimated coefficients from the second step are interpretable, and we then gain valuable insights from an exploratory study. For example, in the application, we concluded that a student with a higher value of the difference between teacher-rated abilities and teacher-reported problems and/or from a family with higher socioeconomic status was more likely to achieve higher mathematics scores (i.e., in Class $2$ and Class $3$).
Although it is not our aim to comprehensively investigate the EFA, we still want to add two notes about factor retention criteria and factor rotation to empirical researchers. Following Fabrigar, Wegener, MacCallum, and Strahan (1999), we used multiple criteria in the application, including the EVG$1$ rule, scree test, and parallel analysis to decide the number of factors; fortunately, all these criteria gave the same decision. Patil, Singh, Mishra, and Todd Donavan (2008) also suggested conducting a subsequent CFA to evaluate the measurement properties of the factors identified by the EFA (if the number of factors is different from multiple criteria).
Additionally, several analytic rotation techniques have been developed for the EFA, with the most fundamental distinction lying in orthogonal and oblique rotation. Orthogonal rotations constrain factors to be uncorrelated, and the procedure, varimax, which we used in the application, is generally regarded as the best one and the most widely used orthogonal rotation in psychological research. One reason for this choice was its simplicity and conceptual clarity. More importantly, we assumed that the constructs (i.e., the factor of the socioeconomic variables and that of teacher-rated scores) identified from the covariates set are independent. However, many theoretical and empirical researchers provided the basis for expecting psychological constructs, such as personality traits, ability, and attitudes, to be associated with each other. Consequently, oblique rotations provide a more realistic and accurate picture of these factors.
One limitation of the proposed two-step model lies in that it only allows (generalized) linear models in the second step. If the linear assumption is invalid, we need to resort to other methods, such as structural equation model trees (SEM trees, Brandmaier et al. (2013)) or structural equation model forests (Brandmaier, Prindle, McArdle, & Lindenberger, 2016) to identify the most important covariates by investigating the variables on which the tree splits first (Brandmaier et al., 2013; Jacobucci et al., 2017) or the output named ‘variable importance’ (Brandmaier et al., 2016), respectively. Note that Jacobucci et al. (2017) pointed out that the interpretations of the FMM and SEM trees are different, and the classes obtained from the SEM tree can be viewed as the clusters of associations between the covariates and trajectories.
One possible future direction of the current study is to build its confirmatory counterpart. Conceptually, the confirmatory model consists of two measurement models, and there exists a unidirectional relationship between the factors of the EFA and the latent categorical variable. Additionally, driven by domain knowledge, the EFA can be replaced with the CFA in the confirmatory model. Additionally, the two-step model is proposed under the assumption that these covariates only indirectly impact the sample heterogeneity. It is also possible to develop a model that allows these baseline covariates to simultaneously explain between-group differences and within-group differences by relaxing the assumption.
Asparouhov, T., & Muthén, B. (2014). Auxiliary variables in mixture modeling: Three-step approaches using mplus. Structural Equation Modeling: A Multidisciplinary Journal, 21(3), 329-341. Retrieved from https://doi.org/10.1080/10705511.2014.915181
Bakk, Z., & Kuha, J. (2017, 11 17). Two-step estimation of models between latent classes and external variables. Psychometrika, 1-22. Retrieved from https://doi.org/10.1007/s11336-017-9592-7
Bandeen-Roche, K., Miglioretti, D. L., Zeger, S. L., & Rathouz, P. J. (1997). Latent variable regression for multiple discrete outcomes. Journal of the American Statistical Association, 440(92), 1375-1386. Retrieved from https://doi.org/10.1080/01621459.1997.10473658
Bartlett, M. S. (1937). The statistical conception of mental factors. British Journal of Educational Psychology, General Section, 28, 97-104.
Bauer, D. J., & Curran, P. J. (2003). Distributional assumptions of growth mixture models: Implications for overextraction of latent trajectory classes. Psychological Methods, 8(3), 338-363. Retrieved from https://doi.org/10.1037/1082-989X.8.3.338
Bishop, C. (2006). Pattern recognition and machine learning. Springer-Verlag.
Blozis, S. A., & Cho, Y. (2008). Coding and centering of time in latent curve models in the presence of interindividual time heterogeneity. Structural Equation Modeling: A Multidisciplinary Journal, 15(3), 413-433. Retrieved from https://doi.org/10.1080/10705510802154299
Boker, S. M., Neale, M. C., Maes, H. H., Wilde, M. J., Spiegel, M., Brick, T. R., … Kirkpatrick, R. M. (2020). Openmx 2.17.2 user guide [Computer software manual].
Bolck, A., Croon, M., & Hagenaars, J. (2004). Estimating latent structure models with categorical variables: One-step versus three-step estimators. Political Analysis, 12(1), 3-27. Retrieved from https://www.jstor.org/stable/25791751
Bouveyron, C., Celeux, G., Murphy, T., & Raftery, A. (2019). Model-based clustering and classification for data science: With applications in r (cambridge series in statistical and probabilistic mathematics). Cambridge: Cambridge University Press. Retrieved from https://doi.org/10.1017/9781108644181
Brandmaier, A. M., Prindle, J. J., McArdle, J. J., & Lindenberger, U. (2016). Theory-guided exploration with structural equation model forests. Psychological Methods, 4(21), 566-582. Retrieved from https://doi.org/10.1037/met0000090
Brandmaier, A. M., von Oertzen, T., McArdle, J. J., & Lindenberger, U. (2013). Structural equation model trees. Psychological Methods, 18(1), 71-86. Retrieved from https://doi.org/10.1037/a0030001
Cattell, R. B. (1966). The scree test for the number of factors. Multivariate Behavioral Research, 1(2), 245-276.
Cattell, R. B., & Jaspers, J. (1967). A general plasmode (no. 30-10-5-2) for factor analytic exercises and research. Multivariate Behavioral Research Monographs, 67(3), 211.
Clogg, C. C. (1981). New developments in latent structure analysis. In D. J. Jackson & E. F. Borgotta (Eds.), Factor analysis and measurement in sociological research: A multi-dimensional perspective (p. 215-246). Beverly Hills, CA: SAGE Publications.
Cook, N. R., & Ware, J. H. (1983). Design and analysis methods for longitudinal research. Annual Review of Public Health, 4(1), 1-23.
Coulombe, P., Selig, J. P., & Delaney, H. D. (2015). Ignoring individual differences in times of assessment in growth curve modeling. International Journal of Behavioral Development, 40(1), 76-86. Retrieved from https://doi.org/10.1177/0165025415577684
Dayton, C. M., & Macready, G. B. (1988). Concomitant-variable latent-class models. Journal of the American Statistical Association, 83(401), 173-178. Retrieved from https://doi.org/10.2307/2288938
Fabrigar, L. R., Wegener, D. T., MacCallum, R. C., & Strahan, E. J. (1999). Evaluating the use of exploratory factor analysis in psychological research. Psychological Methods, 4(3), 272–299. Retrieved from https://doi.org/10.1037/1082-989X.4.3.272
Finkel, D., Reynolds, C. A., Mcardle, J. J., Gatz, M., & Pedersen, N. L. (2003, 06). Latent growth curve analyses of accelerating decline in cognitive abilities in late adulthood. Developmental psychology, 39, 535-550. Retrieved from https://doi.org/10.1037/0012-1649.39.3.535
Goodman, L. A. (1974). The analysis of systems of qualitative variables when some of the variables are unobservable. part i-a modified latent structure approach. American Journal of Sociology, 79(5), 1179-1259. Retrieved from http://www.jstor.org/stable/2776792
Grimm, K. J., Ram, N., & Estabrook, R. (2016). Growth modeling. Guilford Press.
Haberman, S. (1979). Analysis of qualitative data. vol. 2: New developments. New York: Academic Press.
Hagenaars, J. A. (1993). Loglinear models with latent variables. Newbury Park, CA: Sage.
Harring, J. R., Cudeck, R., & du Toit, S. H. C. (2006). Fitting partially nonlinear random coefficient models as sems. Multivariate Behavioral Research, 41(4), 579-596. Retrieved from https://doi.org/10.1207/s15327906mbr4104\_7
Horn, J. L. (1965). A rationale and technique for estimating the number of factors in factor analysis. Psychometrika, 30, 179-185.
Humphreys, L. G., & Ilgen, D. R. (1969). Note on a criterion for the number of common factors. Educational and Psychological Measurement, 29(3), 571–578.
Humphreys, L. G., & Montanelli, R. G. (1975). An investigation of the parallel analysis criterion for determining the number of common factors. Multivariate Behavioral Research, 10(2), 193–205.
Hunter, M. D. (2018). State space modeling in an open source, modular, structural equation modeling environment. Structural Equation Modeling: A Multidisciplinary Journal, 25(2), 307-324. Retrieved from https://doi.org/10.1080/10705511.2017.1369354
Jacobucci, R., Grimm, K. J., & McArdle, J. J. (2016). Regularized structural equation modeling. Structural Equation Modeling: A Multidisciplinary Journal, 23(4), 555-566. Retrieved from https://doi.org/10.1080/10705511.2016.1154793
Jacobucci, R., Grimm, K. J., & McArdle, J. J. (2017). A comparison of methods for uncovering sample heterogeneity: Structural equation model trees and finite mixture models. Structural Equation Modeling: A Multidisciplinary Journal, 24(2), 270-282. Retrieved from https://doi.org/10.1080/10705511.2016.1250637
Kaiser, H. F. (1958). The varimax criterion for analytic rotation in factor analysis. Psychometrika, 23, 187–200. Retrieved from https://doi.org/10.1007/BF02289233
Kamakura, W. A., Wedel, M., & Agrawal, J. (1994). Concomitant variable latent class models for conjoint analysis. International Journal of Research in Marketing, 11(5), 451-464. Retrieved from https://doi.org/10.1016/0167-8116(94)00004-2
Kohli, N. (2011). Estimating unknown knots in piecewise linear-linear latent growth mixture models (Doctoral dissertation, University of Maryland). Retrieved from http://hdl.handle.net/1903/11973
Kohli, N., & Harring, J. R. (2013). Modeling growth in latent variables using a piecewise function. Multivariate Behavioral Research, 48(3), 370-397. Retrieved from https://doi.org/10.1080/00273171.2013.778191
Kohli, N., Harring, J. R., & Hancock, G. R. (2013). Piecewise linear-linear latent growth mixture models with unknown knots. Educational and Psychological Measurement, 73(6), 935-955. Retrieved from https://doi.org/10.1177/0013164413496812
Kohli, N., Hughes, J., Wang, C., Zopluoglu, C., & Davison, M. L. (2015). Fitting a linear-linear piecewise growth mixture model with unknown knots: A comparison of two common approaches to inference. Psychological Methods, 20(2), 259-275. Retrieved from https://doi.org/10.1037/met0000034
Lê, T., Norman, G., Tourangeau, K., Brick, J. M., & Mulligan, G. (2011). Early childhood longitudinal study: Kindergarten class of 2010-2011 - sample design issues. JSM Proceedings, 1629-1639. Retrieved from http://www.asasrms.org/Proceedings/y2011/Files/301090\_66141.pdf
Lehmann, E. L., & Casella, G. (1998). Theory of point estimation, 2nd edition. Springer-Verlag New York, Inc.
Liu, J. (2019). Estimating knots in bilinear spline growth models with time-invariant covariates in the framework of individual measurement occasions (Doctoral dissertation, Virginia Commonwealth University). Retrieved from https://doi.org/10.25772/9WDR-9R85
Liu, J., Perera, R. A., Kang, L., Kirkpatrick, R. M., & Sabo, R. T. (2019). Obtaining interpretable parameters from reparameterizing longitudinal models: transformation matrices between growth factors in two parameter-spaces.
Lubke, G. H., & Muthén, B. O. (2005). Investigating population heterogeneity with factor mixture models. Psychological Methods, 10(1), 21–39. Retrieved from https://doi.org/10.1037/1082-989X.10.1.21
Lubke, G. H., & Muthén, B. O. (2007). Performance of factor mixture models as a function of model size, covariate effects, and class-specific parameters. Structural Equation Modeling: A Multidisciplinary Journal, 14(1), 26-47. Retrieved from https://doi.org/10.1080/10705510709336735
Marcoulides, G. A., & Drezner, Z. (2003). Model specification searches using ant colony optimization algorithms. Structural Equation Modeling: A Multidisciplinary Journal, 10(1), 154-164. Retrieved from https://doi.org/10.1207/S15328007SEM1001\_8
Marcoulides, G. A., Drezner, Z., & Schumacker, R. E. (1998). Model specification searches in structural equation modeling using tabu search. Structural Equation Modeling: A Multidisciplinary Journal, 5(4), 365-376. Retrieved from https://doi.org/10.1080/10705519809540112
McLachlan, G., & Peel, D. (2000). Finite mixture models. John Wiley & Sons, Inc.
Mehta, P. D., & Neale, M. C. (2005). People are variables too: Multilevel structural equations modeling. Psychological Methods, 10(3), 259-284. Retrieved from https://doi.org/10.1037/1082-989x.5.1.23
Mehta, P. D., & West, S. G. (2000). Putting the individual back into individual growth curves. Psychological Methods, 5(1), 23-43.
Morris, T. P., White, I. R., & Crowther, M. J. (2019). Using simulation studies to evaluate statistical methods. Statistics in Medicine, 38(11), 2074-2102. Retrieved from https://doi.org/10.1002/sim.8086
Muthén, B. O., & Shedden, K. (1999). Finite mixture modeling with mixture outcomes using the EM algorithm. Biometrics, 55(2), 463-469. Retrieved from https://doi.org/10.1111/j.0006-341x.1999.00463.x
Neale, M. C., Hunter, M. D., Pritikin, J. N., Zahery, M., Brick, T. R., Kirkpatrick, R. M., … Boker, S. M. (2016). OpenMx 2.0: Extended structural equation and statistical modeling. Psychometrika, 81(2), 535-549. Retrieved from https://doi.org/10.1007/s11336-014-9435-8
Nylund, K. L., Asparouhov, T., & Muthén, B. O. (2007). Deciding on the number of classes in latent class analysis and growth mixture modeling: A monte carlo simulation study. Structural Equation Modeling: A Multidisciplinary Journal, 14(4), 535-569. Retrieved from https://doi.org/10.1080/10705510701575396
Patil, V. H., Singh, S. N., Mishra, S., & Todd Donavan, D. (2008). Efficient theory development and factor retention criteria: Abandon the ‘eigenvalue greater than one’ criterion. Journal of Business Research, 61(2), 162-170. Retrieved from https://doi.org/10.1016/j.jbusres.2007.05.008
Preacher, K. J., & Hancock, G. R. (2015). Meaningful aspects of change as novel random coefficients: A general method for reparameterizing longitudinal models. Psychological Methods, 20(1), 84-101. Retrieved from https://doi.org/10.1037/met0000028
Pritikin, J. N., Hunter, M. D., & Boker, S. M. (2015). Modular open-source software for Item Factor Analysis. Educational and Psychological Measurement, 75(3), 458-474. Retrieved from https://doi.org/10.1177/0013164414554615
R Core Team. (2020). R: A language and environment for statistical computing [Computer software manual]. Vienna, Austria.
Scharf, F., & Nestler, S. (2019). Should regularization replace simple structure rotation in exploratory factor analysis? Structural Equation Modeling: A Multidisciplinary Journal, 26(4), 576-590. Retrieved from https://doi.org/10.1080/10705511.2018.1558060
Seber, G. A. F., & Wild, C. J. (2003). Nonlinear regression. John Wiley & Sons, Inc.
Stegmann, G., & Grimm, K. J. (2018). A new perspective on the effects of covariates in mixture models. Structural Equation Modeling: A Multidisciplinary Journal, 25(2), 167-178. Retrieved from https://doi.org/10.1080/10705511.2017.1318070
Sterba, S. K. (2014). Fitting nonlinear latent growth curve models with individually varying time points. Structural Equation Modeling: A Multidisciplinary Journal, 21(4), 630-647. Retrieved from https://doi.org/10.1080/10705511.2014.919828
Sun, J., Chen, Y., Liu, J., Ying, Z., & Xin, T. (2016). Latent variable selection for multidimensional item response theory models via l1 regularization. Psychometrika, 81, 921-939. Retrieved from https://doi.org/10.1007/s11336-016-9529-6
Thomson, G. (1939). The factorial analysis of human ability. British Journal of Educational Psychology, 9, 188-195.
Tishler, A., & Zang, I. (1981). A new maximum likelihood algorithm for piecewise regression. Journal of the American Statistical Association, 76(376), 980-987. Retrieved from https://doi.org/10.2307/2287599
Tueller, S. J., Drotar, S., & Lubke, G. H. (2011). Addressing the problem of switched class labels in latent variable mixture model simulation studies. Structural Equation Modeling: A Multidisciplinary Journal, 18(1), 110–131. Retrieved from https://doi.org/10.1080/10705511.2011.534695
Venables, W. N., & Ripley, B. D. (2002). Modern applied statistics with s (Fourth ed.). New York: Springer.
Vermunt, J. K. (1997). Advanced quantitative techniques in the social sciences series, vol. 8. log-linear models for event histories. Thousand Oaks, CA, US: Sage Publications, Inc.
Vermunt, J. K. (2010). Latent class modeling with covariates: Two improved three-step approaches. Political Analysis, 18(4), 450-469. Retrieved from https://www.jstor.org/stable/25792024
Yamaguchi, K. (2000). Multinomial logit latent-class regression models: An analysis of the predictors of gender-role attitudes among japanese women. American Journal of Sociology, 105(6), 1702-1740. Retrieved from https://doi.org/10.1086/210470
In the original setting of the bilinear spline model, we have three growth factors: an intercept at $t_{0}$ ($\eta _{0}$) and one slope of each stage ($\eta _{1}$ and $\eta _{2}$, respectively). To estimate knots, we may reparameterize the growth factors. For the $i^{th}$ individual, according to Seber and Wild (Seber & Wild, 2003), we may re-expressed them as the measurement at the knot (i.e., $\eta _{0i}+\eta _{1i}\gamma ^{(k)}$), the mean of two slopes (i.e., $\frac {\eta _{1i}+\eta _{2i}}{2}$), and the half difference between two slopes (i.e., $\frac {\eta _{2i}-\eta _{1i}}{2}$).
Tishler and Zang (1981) and Seber and Wild (2003) showed that the regression model with two linear stages can be written as either the minimum or maximum response value of two trajectories. Liu et al. (2019) extended such expressions to the latent growth curve modeling framework and showed two forms of bilinear spline for the $i^{th}$ individual in Figure A.1. In the left panel ($\eta _{1i}>\eta _{2i}$), the measurement $y_{ij}$ is always the minimum value of two lines; that is, $y_{ij}=\min {(\eta _{0i}+\eta _{1i}t_{ij}, \eta _{02i}+\eta _{2i}t_{ij})}$. To unify the formula of measurements pre- and post-knot, we express $y_{ij}$ as
|
| (A.1) |
where $\eta _{0i}^{'}$, $\eta _{1i}^{'}$ and $\eta _{2i}^{'}$ are the measurement at the knot, the mean of two slopes, and the half difference between two slopes. Similarly, the measurement $y_{ij}$ of the bilinear spline in the right panel, in which the measurement $y_{ij}$ is always the maximum value of two lines, has the identical final form in Equation A.1.
Suppose $\boldsymbol {f}: \mathcal {R}^{3}\rightarrow \mathcal {R}^{3}$ is a function, which takes a point $\boldsymbol {\eta }_{i}\in \mathcal {R}^{3}$ as input and produces the vector $\boldsymbol {f}(\boldsymbol {\eta }_{i})\in \mathcal {R}^{3}$ (i.e., $\boldsymbol {\eta }_{i}^{'}\in \mathcal {R}^{3}$) as output. By the multivariate delta method (Lehmann & Casella, 1998, Chapter 1), for an individual in the $k^{th}$ class
|
| (A.2) |
where $\boldsymbol {\mu _{\eta }}^{[k]}$ and $\boldsymbol {\Psi _{\eta }}^{[k]}$ are the mean vector and variance-covariance matrix of original class-specific growth factors, respectively, and $\boldsymbol {f}$ is defined as
|
|
Similarly, suppose $\boldsymbol {h}: \mathcal {R}^{3}\rightarrow \mathcal {R}^{3}$ is a function, which takes a point $\boldsymbol {\eta }_{i}^{'}\in \mathcal {R}^{3}$ as input and produces the vector $\boldsymbol {h}(\boldsymbol {\eta }_{i}^{'})\in \mathcal {R}^{3}$ (i.e., $\boldsymbol {\eta }_{i}\in \mathcal {R}^{3}$) as output. By the multivariate delta method,
|
| (A.3) |
where $\boldsymbol {\mu }^{'[k]}_{\boldsymbol {\eta }}$ and $\boldsymbol {\Psi }^{'[k]}_{\boldsymbol {\eta }}$ are the mean vector and variance-covariance matrix of class-specific reparameterized growth factors, respectively, and $\boldsymbol {h}$ is defined as
|
|
Based on Equations (A.2) and (A.3), we can make the transformation between the growth factor means of two parameter-spaces by $\boldsymbol {\mu }^{'[k]}_{\boldsymbol {\eta }} =\boldsymbol {f}(\boldsymbol {\mu }^{[k]}_{\boldsymbol {\eta }})$ and $\boldsymbol {\mu }^{[k]}_{\boldsymbol {\eta }} =\boldsymbol {h}(\boldsymbol {\mu }^{'[k]}_{\boldsymbol {\eta }})$, respectively. We can also define the transformation matrix $\boldsymbol {\nabla _{f}}(\boldsymbol {\mu }^{[k]}_{\boldsymbol {\eta }})$ and $\boldsymbol {\nabla _{h}}(\boldsymbol {\mu _{\eta }^{'[k]}})$ between the variance-covariance matrix of two parameter-spaces as
|
|
and
|
|
respectively.
| Para. | Latent Class $1$ | Latent Class $2$ | |
Mean | $\mu _{\eta _{0}}$ | $-0.003$ ($-0.009$, $0.003$) | $0.002$ ($0.000$, $0.007$) |
| $\mu _{\eta _{1}}$ | $0.008$ ($-0.009$, $0.029$) | $-0.009$ ($-0.024$, $0.007$) | |
| $\mu _{\eta _{2}}$ | $0.033$ ($0.007$, $0.098$) | $-0.019$ ($-0.060$, $0.001$) | |
| $\mu _{\gamma }$ | $-0.005$ ($-0.016$, $0.004$) | $0.003$ ($-0.005$, $0.013$) | |
Variance | $\psi _{00}$ | $-0.001$ ($-0.069$, $0.037$) | $-0.016$ ($-0.055$, $0.006$) |
| $\psi _{11}$ | $-0.076$ ($-0.126$, $-0.040$) | $-0.030$ ($-0.083$, $-0.008$) | |
| $\psi _{22}$ | $-0.015$ ($-0.061$, $0.137$) | $-0.057$ ($-0.089$, $0.179$) | |
Path Coef. | $\beta _{0}$ | — | $-0.055$ (NA, NA) |
| $\beta _{1}$ | — | $-0.042$ ($-0.332$, $0.013$) | |
| $\beta _{2}$ | — | $-0.038$ ($-0.332$, $0.019$) | |
| Para. | Latent Class $1$ | Latent Class $2$ | |
Mean | $\mu _{\eta _{0}}$ | $0.432$ ($0.243$, $0.892$) | $0.350$ ($0.200$, $0.707$) |
| $\mu _{\eta _{1}}$ | $0.106$ ($0.053$, $0.294$) | $0.074$ ($0.042$, $0.174$) | |
| $\mu _{\eta _{2}}$ | $0.103$ ($0.052$, $0.280$) | $0.079$ ($0.042$, $0.164$) | |
| $\mu _{\gamma }$ | $0.055$ ($0.024$, $0.167$) | $0.062$ ($0.024$, $0.198$) | |
Variance | $\psi _{00}$ | $2.652$ ($1.731$, $4.817$) | $2.201$ ($1.400$, $3.789$) |
| $\psi _{11}$ | $0.123$ ($0.069$, $0.272$) | $0.092$ ($0.057$, $0.170$) | |
| $\psi _{22}$ | $0.128$ ($0.071$, $0.333$) | $0.101$ ($0.062$, $0.219$) | |
Path
Coef. | $\beta _{0}$ | — | $0.182$ ($0.084$, $0.592$) |
| $\beta _{1}$ | — | $0.120$ ($0.079$, $0.186$) | |
| $\beta _{2}$ | — | $0.124$ ($0.083$, $0.199$) | |
3 $\text {Monte Carlo SE(Bias)}=\sqrt {Var(\hat {\theta })/S}$ (Morris et al., 2019).
4 In our project, convergence is defined as to reach OpenMx status code $0$, which indicates a successful optimization, until up to $10$ attempts with different collections of starting values (Neale et al., 2016).
5 Conditions of these worst cases were the small sample size ($n=500$), unbalanced allocation rate, small residual variance, small distance between the latent classes, and small or medium difference in the knot locations.
6 The total sample size of ECLS-K: 2011 $n=18174$. The number of entries after removing records with missing values (i.e., rows with any of NaN/-9/-8/-7/-1) is $n=1853$.
7 OR ($95\%$ CI) for sex, factor score $1$ and factor score $2$ was $0.345$ ($0.183$, $0.651$), $1.454$ ($1.090$, $1.939$) and $1.656$ ($1.226$, $2.235$), respectively.
8 OR ($95\%$ CI) for sex, factor score $1$ and factor score $2$ was $0.234$ ($0.111$, $0.494$), $2.006$ ($1.408$, $2.858$) and $3.410$ ($2.258$, $5.148$), respectively.