Keywords: Contact networks · Network analysis · Epidemiology · Virus spread · Interventions
The COVID-19 outbreak has underscored the importance of human behavior in controlling virus transmission. As long as vaccines are not operational, the only way to influence transmission rates is through behavioral interventions that either prohibit specific kinds of behavior (e.g., attending school, visiting relatives, leaving the house) or promote others (e.g., physical distancing, wearing masks, complying with regulations). As such, behavior is fundamental to important parameters in epidemiological models, such as the reproduction number (the number of people a randomly chosen disease carrier is expected to infect): even though virus transmission depends on biological characteristics of the virus and the human system, its speed reflects an interaction between biology and behavior (Delamater, Street, Leslie, Yang, & Jacobsen, 2019; Heesterbeek et al., 2015). Indeed, one way of understanding the reasoning behind lockdowns is that they try to drive down the reproduction number by changing behavioral patterns (de Vlas & Coffeng, 2021; Jeffrey et al., 2020). The goal of this paper is to contribute to our understanding of these behavioral patterns, by developing methodological tools that can be used to study them.
To successfully monitor and control our responses to a virus outbreak like COVID-19, we need to obtain insight into the relative effectiveness of different behavioral interventions. Relevant behavioral interventions can either be implemented at a microlevel (e.g., setting up nudges in a store to promote physical distancing, changing the floor plan of a restaurant), or a macrolevel (e.g., implementing public policy measures that promote working from home, closing public buildings). Currently, however, methodology for estimating effects of such interventions at the behavioral level is limited to highly indirect assessments based on measures of virus spread. For example, comprehensive assessments of interventions at the macrolevel (Chu et al., 2020) have been estimated based on the relation between country-level interventions (e.g., school closings, lockdowns) and corresponding population statistics (e.g., hospital admissions, IC uptakes, death rates; see for example Flaxman et al., 2020); or they have been treated as model parameters to assess the time-course of the epidemic under different scenarios – the well-known study by Ferguson et al. (2020), which has played an important role in COVID-19-related policy, is a case in point.
There are at least three methodological reasons why indicators such as hospital admissions are of limited use in assessing effects of behavioral interventions designed to counter virus spread. The first problem is that they are lagged indicators. Evaluating the effect of interventions with hospital admissions as a dependent variable suffers from the time course of virus transmission, incubation, and disease progression, before one can assess where the intervention has been effective (this delay was two to three weeks for COVID-19). The second problem concerns experimental inaccessibility. If one studies an intervention that is strongly suspected to be effective, it is unethical to install a control group for comparison and to wait for participants to become ill. The next best alternative — a quasi-experimental research setup — suffers from considerable levels of confounding, and because interventions are almost always implemented in packages it is hard to disentangle their effects. Third, current indicators require an active virus. Thus, in a period in which there is no virus active, it is impossible to study the effects of behavioral interventions. This is strategically impractical as it would be ideal to study behavioral interventions while the virus is inactive in order to prepare for a possible future outbreak. Moreover, the COVID-19 pandemic is unlikely to be the last global pandemic and research in effective interventions will remain important, even after the current crisis has ended.
The scientific study of behavioral interventions thus requires indicators that are fast, that can be assessed through experiments, and that can be investigated without actual transmission of the virus. In the present paper, we develop a methodological approach designed to deliver such indicators. In a nutshell, we make use of the fact that behavioral data, obtainable through wearable devices, camera data, or tracing apps can be used to assess contact networks (Cencetti et al., 2020). This can either be done at the microlevel (e.g., assessing contact patterns at a public gathering) or at the macrolevel (e.g., reconstructing contact networks at the level of a city on the basis of tracing apps). We coin indicators based on such networks Behavioral Contact Network (BECON) indicators. Because BECON indicators are available in real time, they respond to induced changes in contact networks virtually instantaneously; and because they do not require actual transmission of the virus, they can be used to assess effectiveness in healthy subjects, which in turn means they can be studied in experiments. As such, BECON indicators are suited to make the connection between epidemiology and behavior, and thereby allow behavioral scientists to leverage their knowledge and skills in developing optimal interventions to control the pandemic.
The structure of this paper is as follows. First, we will outline the theoretical basis of our approach. Second, we discuss the methodological strategy behind BECON indicators in more detail. Third, we present a simulation study that serves as a proof of concept. Finally, we discuss future extensions of our work.
To understand the relation between behavior and epidemiology, it is important to introduce an essential mediator in this relation: the contact network. A contact network encodes which people have been sufficiently close to each other to transmit the virus (Newman, 2018; Pastor-Satorras, Castellano, Van Mieghem, & Vespignani, 2015). In contact networks, individuals (or groups of individuals) are represented as nodes, similar to the representation used in well-known social networks. Two nodes are connected by a link if the corresponding individuals have been in sufficiently close prolonged contact for virus transmission to occur, and disconnected otherwise. Exactly what “sufficiently close” means depends on the virus in question. For Ebola, which is only transmissible through bodily fluids (Drazen et al., 2014), a link in the contact network would mean that the corresponding individuals were in direct physical contact. For SARS-CoV-2, a link could be present when two individuals have been within a distance of 1 or 2 meters of each other for some time, given its airborne transmission (CDC, 2020).
Virus spread on a contact network can be conceptualized as a process in which nodes infect each other via the links in the contact network (Pastor-Satorras et al., 2015). Usually, a closed population is divided into epidemiological “compartments”: each individual of the population can be only in one compartment at a time and the compartments describe stages of the disease. Typical examples of compartments include S (susceptible), E (exposed), I (infectious), R (removed, i.e., either cured or deceased) (Keeling & Rohani, 2011). Mathematically, virus spread is a probabilistic process that operates on the contact network topology (Grimmett, 2018; Van Mieghem, 2014) and that specifies infection and curing events, i.e., how long a person is infectious and when the person is cured or deceased. The time distribution of these events, and the local rules at the host (i.e., what happens if a person is in state S, E, I, or R), depend on specifics of the virus in question; for instance, for COVID-19, the consensus during the SARS-Cov-2 variants operative in 2020 held that people were infectious for an average of about 6-7 days (Backer, Klinkenberg, & Wallinga, 2020).
Once the structure of the contact network and the compartment model is specified, the probability or average fraction of individuals in each compartment can be computed per unit time (Sahneh, Scoglio, & Van Mieghem, 2013). If the contact graph does not change too much over time, other global properties of the virus spread can be determined. An important property is the epidemic threshold, which is related to the basic reproduction number $R$ (Pastor-Satorras et al., 2015), and describes the conditions under which outbreaks can occur. If the contact network changes over time, then we enter a complicated situation in which computer simulations are necessary to study virus spread. Another approach is to map the contact graph into a certain class, similar as the classes of Erdős–Rényi or Barabasi-Albert random graphs, and properties of such a contact graph class can be deduced, in principle, analogously (Newman, 2018). Thus, we assume that the time-dependent network has similar properties as the properties of the class and thus abstract the temporal changes in time. Finally, novel approaches based on the analysis of time series data can be used to include the dynamic changes of the network in the analysis (Dekker et al., 2021). In the current paper, we focus on the simplest case, namely one in which the contact network is stable over time so that it can be characterized by a single network structure.

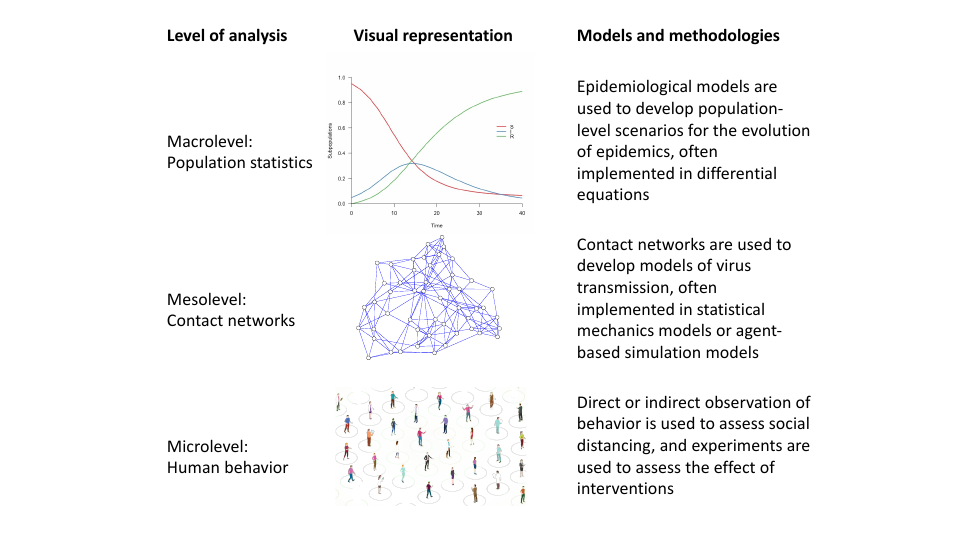
Behavior, contact networks, and compartmental epidemiological models are strongly related: behavior controls the structure of the contact network, the contact network directs the spread of the virus, and the spread of the virus determines population statistics of the epidemiological compartments. Figure 1 represents this hierarchy of levels visually. This has ramifications for how we should think about behavioral interventions: interventions (e.g., instructing people to practice physical distancing) lead to behavior change (e.g., people will keep more distance), which causes contact networks to change (e.g., the number of links in the network may decrease). These changes cascade into population level statistics (e.g., the value of $R$ will go down) that eventually determine policy success (e.g., number of hospital intakes will stay within limits defined in policy considerations). In accordance, a central idea underlying our framework is that, in order to connect interventions to epidemiological models, they should be represented as operations that transform the contact network (Pastor-Satorras et al., 2015); the present paper applies this idea to behavioral interventions.
This analysis opens up an important methodological possibility: if behavioral interventions operate through changes in the contact network, then measures of that contact network could in principle be used to assess the effect of such interventions. Such an approach would address each of the problems highlighted in the introduction. First, assessment of the contact network can be executed instantaneously, addressing the lagging indicator problem. Second, because the contact network depends only on whether individuals are sufficiently close to each other, and not on whether they actually infect each other, we can potentially pick up changes in the contact network in the absence of actual virus transmission (of course, applications of insights gained would still require knowledge of how active transmission works). Third, as a consequence of these two properties, assessments of the contact network can be implemented in experimental designs without raising ethical concerns of exposing individuals to virus spread. As a result, the study of interventions would no longer be limited to assessments of policy effects at the societal level (Chu et al., 2020; Flaxman et al., 2020) but could also be used to study manipulations at a much smaller microlevels (e.g., in specific locations like public buildings, restaurants, or concerts). Implementation at the microlevel in turn facilitates the type of controlled experimental research that characterizes psychology (e.g., the implementation of interventions in factorial designs). In the next paragraph, we show how contact networks may be assessed to construct indicators that allow for such approaches.
The idea behind BECON indicators is to assess (functions of) the contact network on the basis of behavioral observations. In the current paper, we will focus on assessments of the contact network using wearables or contact tracing apps that are designed to register whether a person has been within a certain distance (e.g., 1.5 meters) of another person. This methodology has the advantage that it measures a proxy to actual behavior (rather than, e.g., relying on self-reports) and that it does not require a controlled environment, so that it can in principle be used in daily life, enhancing ecological validity.
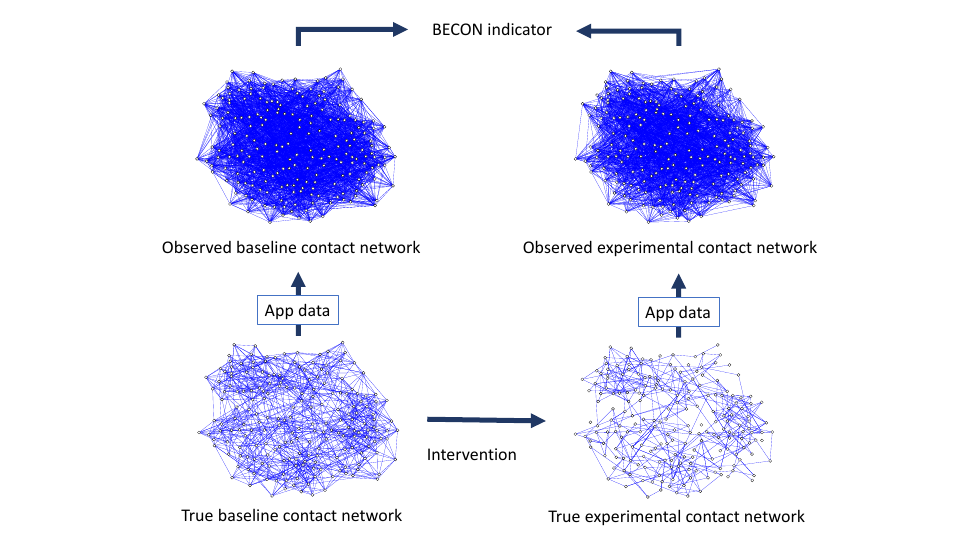
A schematic of the proposed methodology is represented visually in Figure 2. The interactions between people in the baseline situation (i.e., the situation without the behavioral intervention of interest being implemented) give rise to the true baseline contact network (left bottom).
The true contact network is most likely not directly observable. First, as noted, the presence of a link depends on a theory of virus transmission, which is approximate. For example, in the case of COVID-19, the presence of aerosol transmission or infection via surfaces can create links between people who are at a greater distance than 1.5 meters, or between people who were present at the same place at distinct time points (e.g., because the aerosols remain present in bathrooms after the infectious person has left). Second, if the network integrates contacts over time (e.g., by taking the union of all contact networks at each time point, which registers during a certain time interval who has ever been in contact with who, but not when), the representation will contain false positive connections; for instance, when $A$ and $B$ were in contact, and subsequently $B$ and $C$ were in contact, then the patterns of links suggests that both $A \rightarrow B \rightarrow C$ and $C \rightarrow B \rightarrow A$ are possible infection routes, while only the former route is possible (see also Dekker et al. (2021)). Third, various kinds of measurement errors can yield false positives and false negatives. In a situation in which tracking devices are used, examples of mechanisms that can lead to measurement errors may include hardware failures, signal failures, and failures in data processing.
Thus, the true baseline contact network is generally not observable and difficult to assess adequately. In the present paper we therefore represent this network as a latent structure. To assess this latent structure, we can use observations, as for instance obtained through smartphone apps, video footage analysis, or wearable sensors. For instance, a simple starting point may be to have a group of people use wearable devices that track their location. Measured location data may then be used to decide whether two people have been in contact. Thus, the structure of the data required to construct a contact network is of the form $[AB, BC, \ldots , YZ]$ which encodes that persons $A$ and $B$, $B$ and $C$, $\ldots $, and $Y$ and $Z$ have been within 1.5 meters of each other for the amount of time specified in the definition of a contact. This is called an edge list in network science, which can be transformed into an adjacency matrix. From this matrix, many important metrics in network analysis can be computed (Newman, 2018). We denote the network encoded in the empirically derived adjacency matrix the observed baseline contact network (top left in Figure 2).
Next, we implement a behavioral intervention. For example, we might instruct people to keep their distance, put up signposts, install an alarm on their phones that sounds when they get too close, or use a variety of nudges that promote physical distancing. If effective, the intervention changes people’s behavior, and as such induces changes in the contact network. We denote the resulting network as the true experimental contact network. Like the baseline contact network, the true experimental contact network is not directly observable, but can be assessed indirectly through location measurements. Such data may again be obtained by letting people use wearables in the experimental situation, after which the results can be used to arrive at an observed experimental contact network.
Recall that a behavioral intervention effect is, in essence, a transformation of the contact network. Hence, if we could directly assess the baseline and experimental contact networks, we could precisely determine the effect of the intervention and, given a dynamical regime, we could also assess the degree to which the intervention should be expected to mitigate virus spread. Unfortunately, however, we cannot directly compare the baseline and experimental networks, as these are only indirectly observable. However, we can directly compare the observed networks created through measurements. For example, one could compute the number of links in the observed experimental contact network, and compare that quantity to the number of links in the observed baseline network. This way, one could assess whether, on average, people keep more distance in the experimental condition. From a bird’s eye perspective, observational studies have shown a substantial decline in average mobility after lockdowns have been enforced (e.g., Jeffrey et al., 2020). However, one could also utilize a variety of more advanced network metrics which can provide a detailed picture of the changes that the intervention has produced. For example, one could compare the networks for their density, diameter, average shortest path lengths, etc. to assess the effect of specifically targeted interventions (e.g., interventions that target specific individuals central in the contact network, like doctors and teachers).
The function that is chosen to assess the difference between networks defines a Behavioral Contact Network indicator; a BECON. In this paper, we develop three BECONS: The Density BECON, the Spectral BECON, and the ASPL BECON. To facilitate interpretation, each of the BECON indicators is constructed in such a way that a higher value on the indicator implies that the experimental network has changed the network in a direction that would in typical circumstances be expected to limit the potential for a virus to spread. The indicators studied here are are defined as follows.
The Density BECON uses the relative change in network density. Network density is defined as the ratio of the number of links to the total number of possible links in the network. This measure is epidemiologically relevant, because denser networks indicate that more people have been in close proximity to each other. The Density BECON is constructed by dividing the density of the observed baseline contact network by that of the observed experimental contact network, where higher values indicate larger experimental effects. In essence, this measure simply tracks the extent to which the number of contacts reduces in the experimental condition. This measure would be most relevant in microlevel applications, where people for instance use wearables during a public event, because in this case only the direct contacts are relevant. This is because for COVID-19, a person will take several days from infection to being infectious; hence, indirect connections that would lead to transfer from one person to another via a third person ($A \rightarrow B \rightarrow C$) are not possible on such short time-scales. This metric is particularly suitable in microlevel applications when the period from infection to being infectious takes multiple days, as was the case with COVID-19. In this situation, indirect connections that would leads to transfer from one person to another via a third person ($A \rightarrow B \rightarrow C$) are not possible and, hence, the (dynamical) contacts can be concatenated into a single contact network.
The Spectral BECON is based on the spectral radius. The spectral radius is the largest eigenvalue of the adjacency matrix. The spectral radius is epidemiologically important, because the inverse of the spectral radius is equal to the so-called mean-field epidemic threshold, which is in turn a lower bound to the real epidemic threshold (Van Mieghem & Van de Bovenkamp, 2013; Van Mieghem & van de Bovenkamp, 2015). The epidemic threshold plays a central role in networks and copes with structural heterogeneity, because a viral strength above the epidemic threshold will endemically infect a non-zero fraction of the nodes in the network. In the limiting case of a complete graph on $N$ nodes, where all nodes are connected to each other, the epidemic threshold is approximately equal to $1/N$ and the strength of the virus divided by the epidemic threshold is approximately equal to the reproduction number, whose critical value is equal to one (for a reproduction number larger than one, the model predicts the virus to be endemic, while for values below one it predicts that the virus will eventually disappear). Moreover, one may control and tune the contact network so that its spectral radius is minimized and the vulnerability for infections (virus spread) is maximized (Van Mieghem et al., 2011). The Spectral BECON is constructed by dividing the largest eigenvalue of the adjacency matrix of the observed baseline contact network by that of the observed experimental contact network, such that a larger value indicates a larger intervention effect. The Spectral BECON would not be relevant in microlevel research (e.g., tracking people in a location over several hours), but rather would apply to measures taken over days, as could be gained using contact tracing apps. A specific example would be contact tracing within the workspace, where the same group of people met each other over longer periods of time. Different set-ups and interventions could be tried out (e.g., different ‘bubbles’ of employees, different organisation of common spaces, walking routes), and their effectiveness could be assessed using the Spectral BECON. The Spectral BECON is thus useful to assess intervention effects that involve changes in the network structure that not only affect the number of links per node, but work on the architecture of the network as a whole.
The ASPL BECON uses the average shortest path length (ASPL) between pairs of nodes in the network. The shortest path length (SPL) between two nodes equals the minimum number of edges that one has to traverse to travel from one node to the other; the ASPL is the average value of all SPLs between all pairs of network nodes. The ASPL is relevant to virus transmission, because the shorter the paths that connect nodes in a contact network are, the easier the virus can spread from one person to randomly chosen other person. The ASPL BECON is constructed by dividing the ASPL of the observed experimental contact network by that of the observed baseline contact network. Like the Spectral BECON, the ASPL BECON could be applied in research where contacts are traced over a period of days, in which indirect connections ($A \rightarrow B \rightarrow C$) are relevant. For calculation of the ASPL BECON we ignore any infinite shortest path lengths that arise from disconnected graphs (i.e., in the case when some nodes or groups of nodes are unconnected). Thus if there was more than one single connected component (which happened in less than 3% of the cases), paths between nodes in different connected components did not exist. We hence ignored these when computing the ASPL BECON.
The fact that each is expressed as a ratio allows one to interpret the BECON values directly: for instance, if the Density BECON equals 2, this means that the density of the observed baseline contact network is twice as large as that of the observed experimental contact network. Other things being equal, a higher BECON value would indicate that the intervention would likely be more successful in mitigating virus spread (naturally, this should be considered in the light of a theory about the virus transmission process). In research at the microlevel, where people are traced over periods of hours, the Density BECON would be most relevant.
An important methodological question is whether we can use BECON indicators to assess the effect of interventions in realistic circumstances, where our assessments of the contact network will be distorted in various ways. Thus, the question that arises is whether the setup sketched in Figure 2 can be used to assess the effect sizes of experimental manipulations in realistic conditions. For example, can one order the effects of a set of behavioral interventions in terms of effect size? How does the methodology fare in the presence of realistic amounts of measurement error? To assess whether this is indeed possible, we now turn to a simulation study.
The simulation study is designed to evaluate whether the BECON methodology is indeed able to pick up effects of interventions if these are present. To show this, we vary the size of intervention effects on the true contact network, and subsequently assess the corresponding BECON values in the observed contact network which is subjected to various levels of noise. If the method is reliable, we expect the BECON values to be higher if the effects are stronger. We evaluate this by computing the correlation between the size of the simulated intervention effect and the observed BECON values: the higher the correlation is, the more reliable the BECON is as an indicator of intervention effects.
In the simulation, we vary the number of nodes in the network $n \in $ [100, 200, 500, 1000], specifying the architecture of the contact network as a small world structure (Watts & Strogatz, 1998) and generate it using the R package igraph (Csardi & Nepusz, 2006), with a neighborhood size of $K = 5$ and a rewiring probability of $p = 0.10$. We use this specification because it leads to a network structure with a high degree of clustering yet small average shortest path lengths, which is qualitatively similar to the structure of some social networks found in empirical research, where links may e.g., encode whether individuals work at the same place or visit the same sports club. This network serves as our baseline contact network (Figure 2, left bottom).
Next, we simulate a measurement process (Figure 2, left arrow). The process generates imperfect measures of the baseline contact network. We simulated a measurement function with a false negative rate of $fn = [0.10, 0.20, 0.30]$ (e.g., $fn = 0.30$ implies that only $70\%$ of the network links were successfully picked up) and false positive rate $fp = [0.10, 0.20, 0.30]$ (e.g., $fp = 0.10$ implies that $10\%$ of the links that are absent in the true contact network will be present in the observed network). We emphasize that, in the present paper, our interest is not to retrieve the actual network structure by correcting for these distortions or to recover the dynamical processes that it supports. Instead, our primary interest here lies in the pragmatic goal of assessing the effect of interventions, so as to develop an indicator that can serve to bridge the gap between epidemiology and behavioral science.
Subsequently, we assess the observed baseline contact network using the obtained data (Figure 2, top left). This network can be quite severely distorted as a result of the probabilistic nature of the measurement function. For instance, as is visible in the figure, the observed network is much denser than the true contact network, even though the false positive rate is much lower than the false negative rate. This is because the true contact network is relatively sparse, which means it contains more absent than present links: the small world networks we generated for $n = 100$ individuals have $n \times (n - 1) / 2 = 4,950$ possible links, of which on average only $K \times n = 500$ are actually present. Hence, a false positive rate of $10\%$ generates about $0.10 \times (4,950 - 500) = 445$ false positive links, while the false negative rate of $30\%$ means that on average only $350$ of the $500$ actual links are successfully identified. In other words, the observed baseline contact network contains about $445 + 350 = 795$ links, of which only $350$ are true positives. Because links feature such a low base rate, the probability that two nodes that are connected in the observed network are actually connected in the true contact network is only $350/795$, i.e., about $0.44$. This effect is stronger in larger networks, because in larger networks there are more opportunities for false positives; for example, in a network of $1000$ individuals, the probability that an observed link is actually present in the true network is only $0.07$. Thus, the actual assessment of the network in itself may be largely unsuccessful, especially in larger networks. We think that similar results would be expected in actual empirical work if the studied contact networks are sparse. However, as we will see, the lack of success in assessing the contact network itself does not preclude the possibility of assessing intervention effects by comparing the observed networks.
We now implement an intervention on the network (Figure 2, bottom arrow). A typical intervention would be intended to, e.g., improve physical distancing, and hence should lead to a lower connectivity in the experimental contact network (Figure 2, bottom right). We model such an intervention by deleting links uniformly at random (a process known as bond percolation in the network literature; Newman, 2018). The proportion of links deleted from the baseline contact network then defines the effect size of the intervention. We vary this effect size in steps of $10\%$, from an ineffective intervention, which deletes no links, to the strongest intervention, which deletes $90\%$ of the links. We implement this intervention in two ways: the deterministic intervention removes the specified proportion of links exactly, by randomly deleting links until this proportion is reached, while the probabilistic intervention removes each link with a probability equal to the specified proportion. Thus, in an intervention setting with effect size of, say, $0.40$, the deterministic intervention results in a network where exactly $40\%$ of the links are deleted, while the probabilistic intervention removes each link with a probability of $0.40$, so that the expected percentage of removed links equals $40\%$ while each realization may be different. The probabilistic intervention thus implements a situation in which the interventions are represented as a random effect that differs across experimental settings, leading to more uncertainty. Importantly, these interventions are but two of the many alternative and possibly directed interventions that one may study (Trajanovski, Martín-Hernández, Winterbach, & Van Mieghem, 2013).
Finally, we implement the same measurement function as before on the experimental contact network. This way, we arrive at the observed experimental network (Figure 2, top right). As was the case for the baseline contact network, this assessment is dominated by false positives, which leads to a significant overestimation of the network density. In addition, the fact that the experimental contact network is sparser than the baseline contact network implies that the probability of a link being present in the experimental network, given that it is present in the observed experimental network, has diminished even more.
| $n$ | FP | Deterministic | Probabilistic
| |||||||||||
Density | Spectral | ASPL | Density | Spectral | ASPL
| |||||||||
$r$ | $SD$ | $r$ | $SD$ | $r$ | $SD$ | $r$ | $SD$ | $r$ | $SD$ | $r$ | $SD$
| |||
| 100 | 0.1 | 1 | 0 | 1 | 0 | 1 | 0 | 0.97 | 0.03 | 0.96 | 0.04 | 0.97 | 0.03 | |
| 100 | 0.2 | 1 | 0 | 1 | 0 | 1 | 0 | 0.92 | 0.05 | 0.92 | 0.06 | 0.92 | 0.05 | |
| 100 | 0.3 | 1 | 0 | 1 | 0 | 1 | 0 | 0.86 | 0.10 | 0.86 | 0.10 | 0.85 | 0.11 | |
| 200 | 0.1 | 1 | 0 | 1 | 0 | 1 | 0 | 0.97 | 0.03 | 0.96 | 0.03 | 0.97 | 0.02 | |
| 200 | 0.2 | 1 | 0 | 1 | 0 | 1 | 0 | 0.92 | 0.06 | 0.91 | 0.06 | 0.91 | 0.06 | |
| 200 | 0.3 | 1 | 0 | 1 | 0 | 1 | 0 | 0.86 | 0.10 | 0.85 | 0.10 | 0.85 | 0.11 | |
| 500 | 0.1 | 1 | 0 | 1 | 0 | 1 | 0 | 0.96 | 0.03 | 0.96 | 0.03 | 0.97 | 0.02 | |
| 500 | 0.2 | 1 | 0 | 1 | 0 | 1 | 0 | 0.92 | 0.07 | 0.92 | 0.06 | 0.91 | 0.07 | |
| 500 | 0.3 | 1 | 0 | 1 | 0 | 1 | 0 | 0.85 | 0.11 | 0.84 | 0.11 | 0.84 | 0.11 | |
| 1000 | 0.1 | 1 | 0 | 1 | 0 | 1 | 0 | 0.96 | 0.03 | 0.96 | 0.03 | 0.96 | 0.03 | |
| 1000 | 0.2 | 1 | 0 | 1 | 0 | 1 | 0 | 0.91 | 0.06 | 0.91 | 0.06 | 0.91 | 0.06 | |
| 1000 | 0.3 | 1 | 0 | 1 | 0 | 1 | 0 | 0.85 | 0.10 | 0.85 | 0.10 | 0.85 | 0.10 | |
As a measure of the accuracy of the BECONs in ordering the intervention effect sizes, we compute the average correlation between the estimated BECONs and the actual intervention effect across simulation runs. A correlation of unity then means that the BECONs order the interventions perfectly, while a correlation of $0$ means that the BECONs do no better than chance.
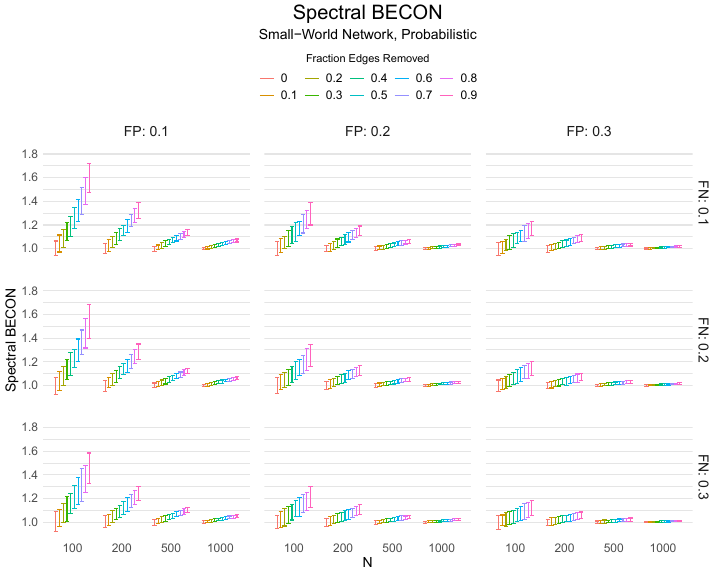
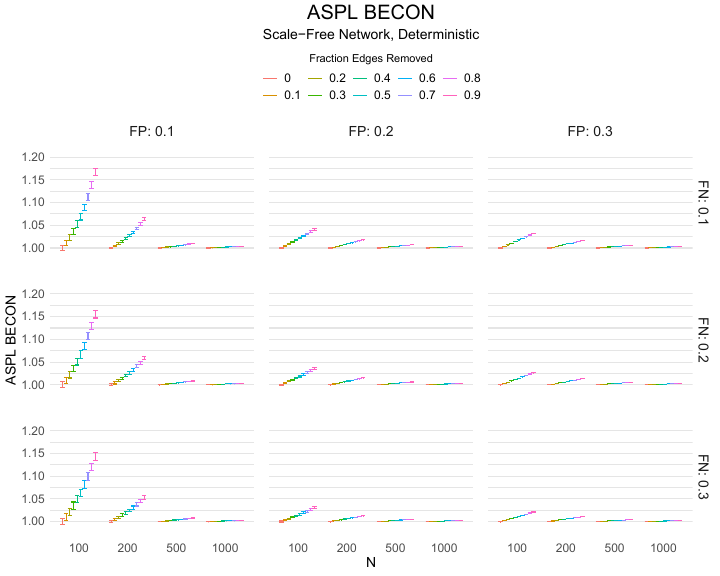
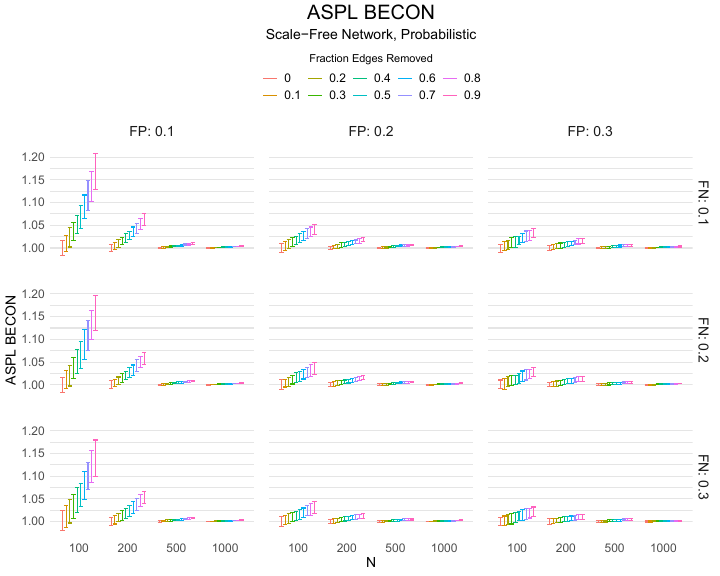
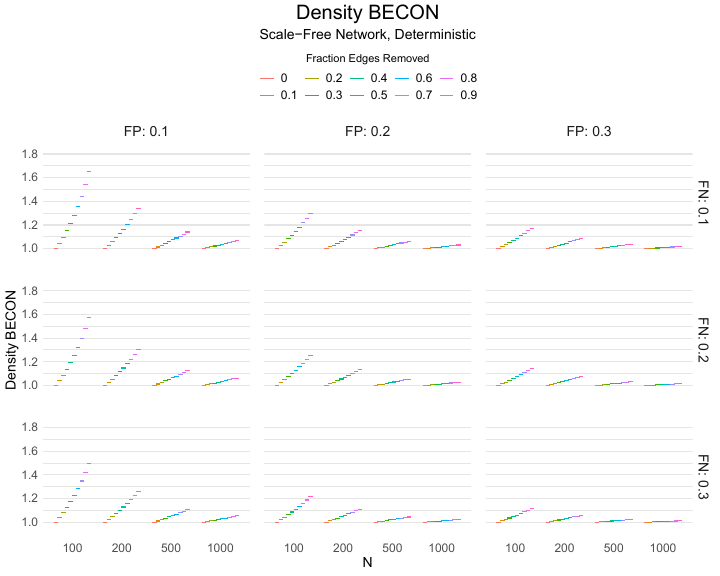
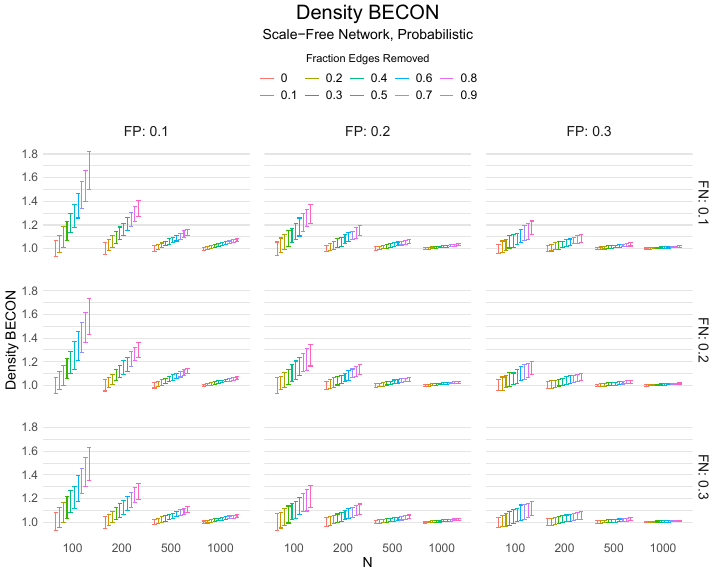
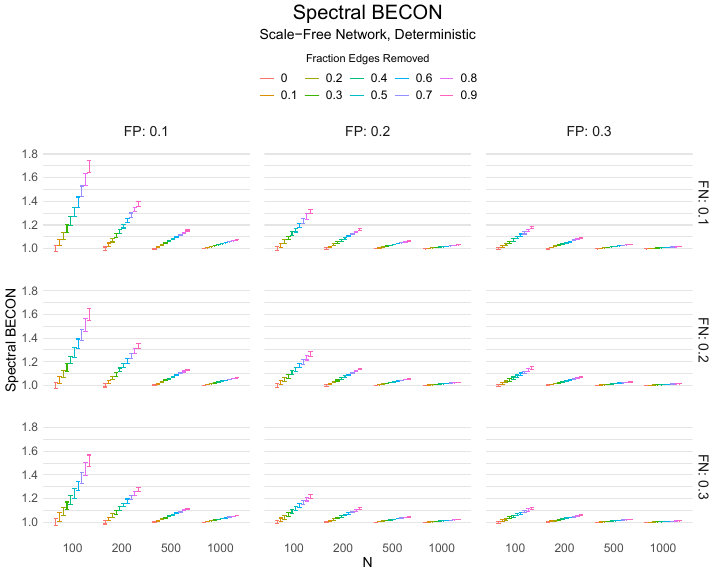
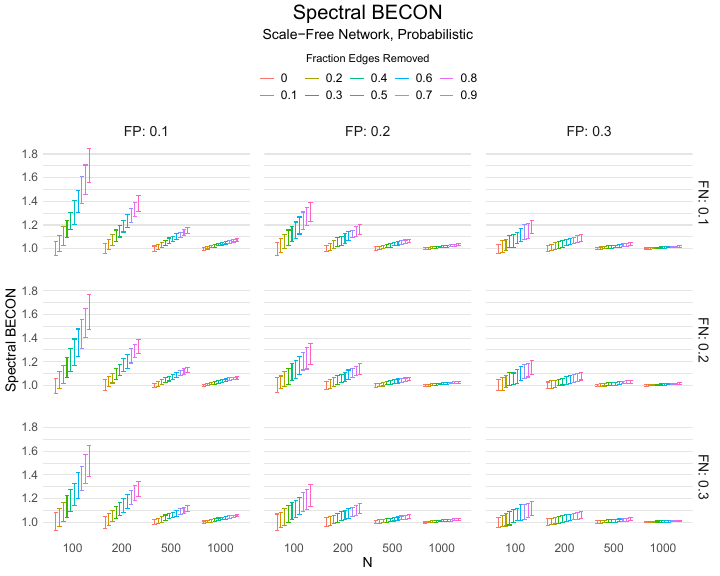
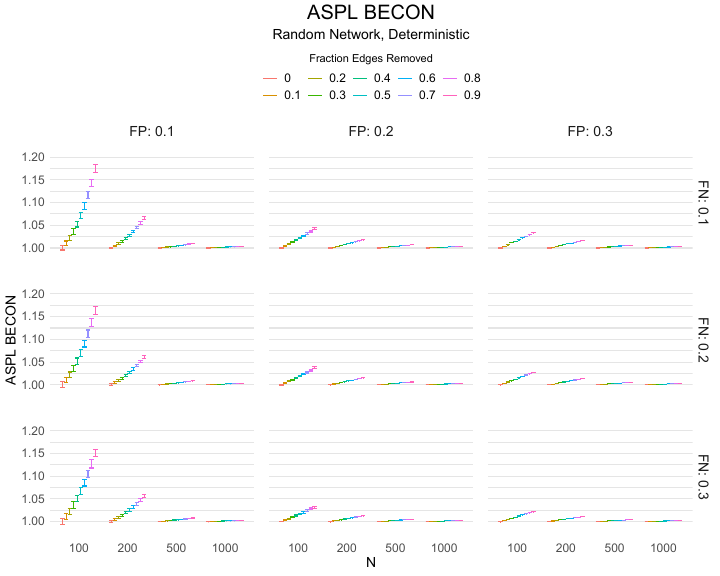
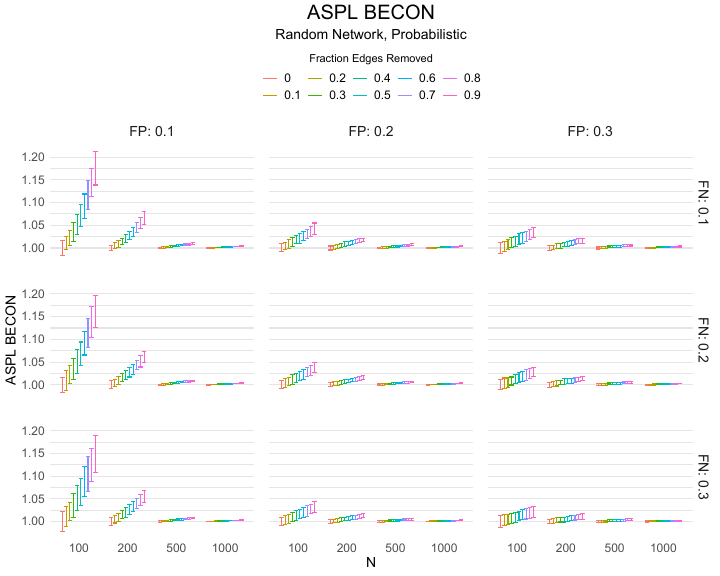
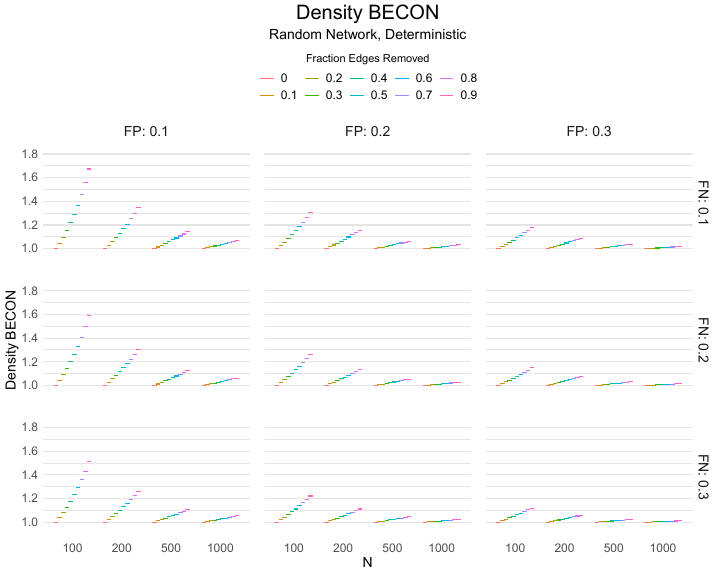
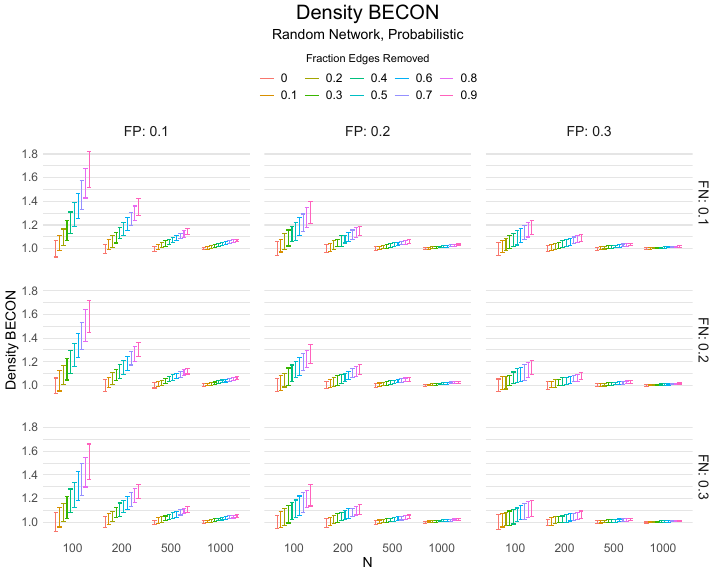
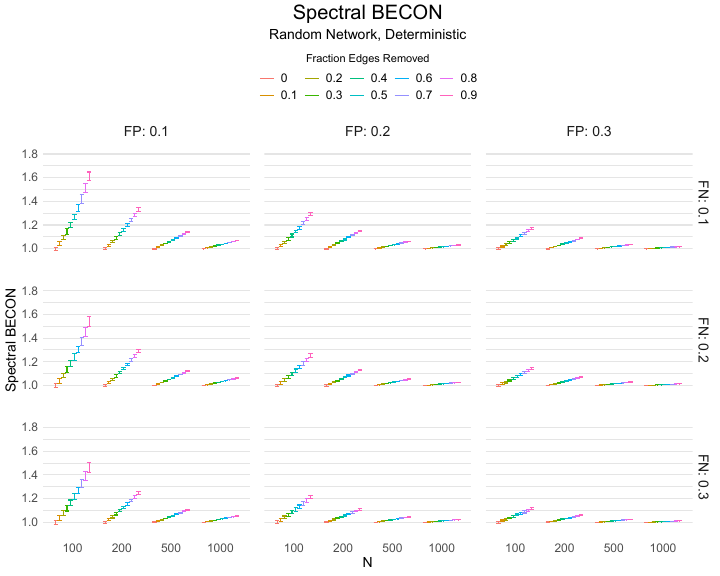
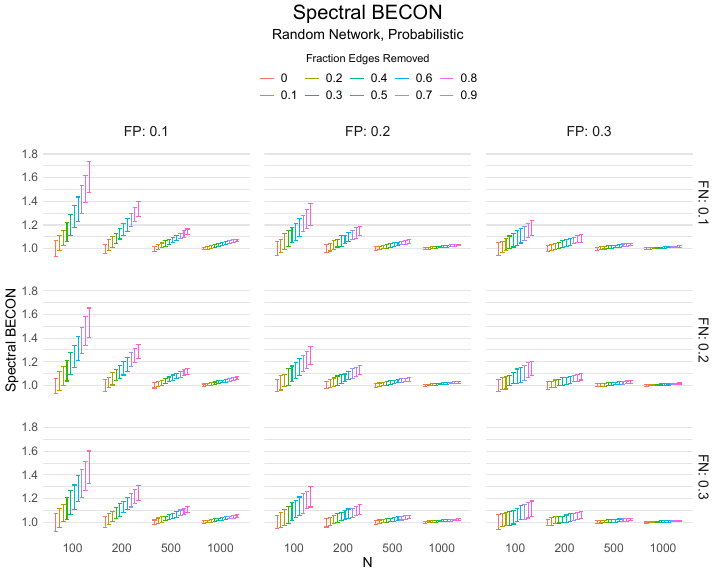
Results of the simulations are given in Table 1. As can be seen from the table, despite the fact that the networks used to compute the BECONs were poor representations of the actual contact networks, the difference between the observed networks tracks the intervention effect size reliably. To illustrate how these effects arise, Figure 3 gives a detailed representation of results for one specific BECON in the simulation design, i.e., the ASPL BECON performance with $fp = 0.20$ and $fn = 0.20$. Detailed representations of simulation results for all BECONs across all conditions are given in the Appendix. As shown in detail in the Appendix, the results in Figure 3 are representative of the behavior of all three BECONs, which uniformly varied as a monotonic function of effect size, in the sense that the probability distributions of these statistics stochastically order the interventions. The separation of effect sizes is in fact perfect for all deterministic intervention simulations. In the probabilistic intervention simulation, results are somewhat more attenuated, but the correlation between true and estimated intervention effects does not drop below $0.80$. Thus, even with sizeable false positive and false negative rates, the methodology still works extremely well.
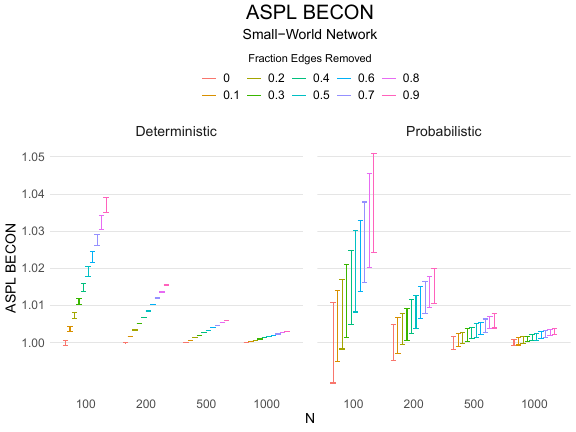
As can be seen in Figure 3 and the extended results in the Appendix, BECONs are monotonically related to intervention effect sizes, such that stronger effects result in higher BECONs. Yet, for larger networks, the increase in BECON attenuates (i.e., the slope becomes smaller). This can be explained by the small world structure of the networks, which makes larger networks relatively more sparse compared with smaller networks. As a result, a fixed false positive rate in the measurement process (e.g., $20\%$ false positives) has a more pronounced effect in the larger networks. This is because the number of present links grows linearly with the number of nodes, while the number of possible links grows quadratically, and therefore larger networks feature a smaller percentage of present links. For example, a neighborhood size of $5$ results in the presence of about $1\%$ of the possible links in a network of $1000$ people ($5,000$ out of $449,500$), but the presence of about $10\%$ of the possible links in a network of $100$ people ($500$ out of $9,900$). As this measurement process applies to both the observed baseline network and to the observed experimental network, the false positive rate will make larger networks relatively more similar to each other than smaller networks. Consequently, it is more difficult to detect an effect in larger networks, which is reflected in the BECONs. However, as is evident from Table 1, BECON performance is robust against this effect across the conditions simulated.
Finally, we find essentially the same results for a scale-free network, that is, a network whose degree distribution follows a power law, and for an Erdős–Rényi random graph, which has a binomial degree distribution. Results for these network structures as well as code to reproduce them are available at https://gitlab.com/science-versus-corona/becon. Performance is broadly consistent across network structures. The reason for this may lie in the noisy measurement process: the false positive rate results in a substantial amount of new links, which obscure the original structure and thereby may counter effects of network structure.
In this paper, we have introduced a behavioral data science methodology to study interventions designed to counter virus spread, and have shown in simulations that this methodology is both feasible and effective. BECON indicators, constructed to pick up changes in the contact network that are induced by interventions, were shown to track intervention effects reliably under realistic measurement conditions that are characterized by substantial levels of noise. Thus, BECON indicators offer a promising methodological approach to studying interventions designed to mitigate virus spread in COVID-19 and other infectious diseases.
Because BECON indicators are instantaneous and can be constructed in the absence of actual virus spread, they address the main problems that plague widely used indicators, such as hospital admissions and death rates. In contrast to current indicators, BECON indicators do not suffer from lags and can be used in experimental designs; in addition, if used in the absence of actual virus transmission, the use of BECON indicators need not put participants in control conditions at risk. Therefore, BECON indicators have the important advantage that they can be used when viruses are not present, i.e., they allow us to maximize our defenses and to prepare for new outbreaks. Of course, the interpretation of the results does depend on details of the virus transmission process, and an important question is how to relate changes in the observed contact networks to this process.
As indicated, the study of which BECON is best suited for a given research question depends on a combination of factors including characteristics of the virus, properties of the research design, and the goals of the research program. One important issue, highlighted throughout this manuscript, involves the time scale at which the research program runs in relation to the time scale at which a virus spreads. In cases where people are observed for a shorter time than that needed for the virus to incubate and become infectious, the Density BECON is always best, because the virus cannot travel more than a single step in the network. In cases where people are followed for a period that exceeds this period, the Spectral and ASPL BECONs become feasible alternatives. If one wants to study effects of generic interventions (e.g., lockdowns or school closures) on virus spreading potential, then the Spectral BECON is indicated due its close relation to the epidemic threshold (Van Mieghem & Van de Bovenkamp, 2013; Van Mieghem & van de Bovenkamp, 2015). Finally, in cases where one has interventions that are specifically targeted at the path lengths in the network (e.g., interventions targeted to limit interactions based on a previous interaction history), one can use the ASPL BECON. Thus, generally, we would recommend the Density BECON in all situations where the research design observes behavior at a duration below that needed for the virus to spread, and the Spectral and ASPL BECONs in research designs that observe behavior for longer durations; the choice between Spectral and ASPL BECONs then depends on specifics of the research question.
The Density BECON offers a simple metric to be used in small scale experiments, where one for instance wants to test the effectiveness of office designs in a company, or where one desires to assess the relative effect of different nudges. We performed a study in which we applied the BECON methodology in practice. During an art fair, we implemented different nudges and evaluated its effect on the contact network. This way we could for example show that walking directions positively impacted physical distancing and reduced the number of contacts, demonstrating the effectiveness of the proposed methodology in practice (Blanken et al., 2021; Tanis et al., 2021). Simulations indicate that even for small networks the indicators are reliable. However, BECON indicators are potentially also applicable to large scale research. For example, using contact tracing apps, it should be possible to assess contact networks at the scale of neighborhoods, cities, or even countries. Thus, BECON indicators could be implemented in a dashboard used by policy makers to assess the degree to which current policies are on track. Because they are much faster than traditional indicators, they may also be highly useful in contributing to alarm systems that indicate that policy action is required.
While our approach aims to change the network structure by deleting links, a closely related notion is the removal of nodes (known as site percolation; Newman, 2018). This is especially important in vaccination campaigns, especially if vaccinating an individual leads to a situation where the vaccinated individual cannot receive nor spread the disease (Y. Liu et al., 2021).3 Strictly speaking, vaccinating an individual does not change the network structure. For the purposes of disease spreading, however, one may reformulate it as such: in cases where vaccinating an individual ensure that the individual will no longer be able to spread the disease, this implies that all links going into and out of the node will be removed. Although it focuses on node rather than link removal, research done on animal populations is related to the approach we propose here. Carne, Semple, Morrogh-Bernard, Zuberbuehler, and Lehmann (2013), for example, use simulations to study how targeted vaccination (e.g., vaccinate the most central nodes) outperform random vaccination in a network derived from observations of orangutans and chimpanzee populations, respectively. They used cluster size and shortest paths of the network as measures to assess the effect of interventions (see also Albert, Jeong, & Barabási, 2000). Relating the network structure to the final outbreak size, Rushmore et al. (2014) find in simulations that vaccinating the most connected chimpanzees can reduce the outbreak size considerably. While these articles focus on node removal, we expect that our approach can learn from such approaches; future research may explore this line more fully.
Several limitations to the present work should be noted. For example, as we have emphasized throughout this paper, observed networks will ordinarily be poor representations of the contact networks of interest unless contact network assessments are augmented by more advanced measurement methods. Therefore, one should be very careful in using observed contact networks as proxies for the underlying contact networks. For example, the fact that observed networks are likely to be much more dense than the underlying contact networks suggests that it would not be a good idea to use these observed networks naively in, e.g., simulations of virus transmission. However, our primary interest in this paper was not in the reconstruction of contact networks per se, but in the comparison of contact networks across experimental conditions. Standard experimental wisdom holds that errors in observations need not form an insurmountable problem as long as the structure and size of the induced distortions is comparable across experimental conditions; in this case, systematic errors will be invariant across conditions, and random errors will average out as the number of observations grows. This indeed is shown to be the case in our simulations. It should be noted that more advanced reconstruction methods may lead to biases if they are differentially effective across conditions, so a better reconstruction need not imply a better signal of intervention effectiveness.
Our approach invites improvements at several points. First, we study a simple measurement process. In the real world, it is likely that the observed network is not biased in a manner as we study here (i.e., by adding false positives and false negatives), but that more complicated biases occur as would, for example, arise when the structure of missing data depends on the network structure itself. Such biases can be addressed by adding an intermediary network reconstruction step. In particular, before computing the BECONs, one can use network reconstruction algorithms to first arrive at a better representation of the true network (e.g., Clauset, Moore, & Newman, 2008; Ghasemian, Hosseinmardi, Galstyan, Airoldi, & Clauset, 2020; Goyal & Ferrara, 2018; Guimerà & Sales-Pardo, 2009). Similarly, the use of additional sources of information deliverable through mobile phones (e.g., geographical location data, WIFI data, ultra wide-band technology) could enhance the precision of the signal (Trofimenko, Mukhina, & Visheratin, 2016). In addition, if the amount of bias in the measurement function is not equal across experimental conditions, the presented methodology would likely lead to incorrect conclusions. Because of the sparsity of the contact networks, even differences in random noise could potentially lead to bias in the effect sizes under certain conditions. For example, if the experimental intervention increases the percentage of false negatives, it can seem effective while it is not. Statistical corrections could be developed on the basis of latent variable models, which are able to accommodate violations of measurement invariance to some extent (Meredith, 1993; Van De Schoot et al., 2013).
Another open question is whether the validity of BECONs is symmetric; can we pick up interventions that make the network more densely connected as easily as interventions that prune it? This is an important question in the process of monitoring lifting regulations, which is expected to create increasingly connected contact networks. BECON methodology could be used to assess the relative risk of different lifting interventions experimentally, and as such may inform exit strategies.
Given that the value of the BECON methodology especially lies in its ability to tap into actual (distancing) behavior, we hope the present paper contributes to experimental research into the effectiveness of behavioral interventions in this domain. However, the interventions we have studied in this paper are very simple, as they delete links at random. One may interpret such an intervention as reducing contacts at random. It would be interesting to investigate what happens if an intervention does not randomly delete links, but affects the structure of the network in a different way (as for example in Trajanovski et al., 2013). For example, one could examine what happens if interventions selectively take out shortest paths, but keep clusters (e.g., groups of friends) intact. This would probably change not only the density, but also the structure of the contact network after intervention; for example, selectively targeting nodes with high centrality may lead the network to lose its small world character. These interventions would have considerable effect on epidemic spread. One such investigation was recently provided by Block et al. (2020). The authors study three types of interventions — limiting social interactions to a few individuals, seeking similarity across contacts, and strengthening communities — that change the contact network. They subsequently simulate virus spread and find that all three interventions substantially flatten the infection curve compared to no intervention, as well as to an intervention that makes actors randomly reduce their contacts (i.e., removes links at random). As suggested above, this shows that more thoughtful interventions can have a more drastic effect on virus transmission. Since different interventions change the contact network in different ways, it is important to choose the right BECON. In addition, such thought experiments suggest that the question under which conditions which BECONs can adequately track virus transmission is open for future research; one could imagine, for instance, implementing different interventions and running epidemiological virus spread models on the resulting networks to understand how different interventions change the epidemiological course of the virus. Finally, the current setup ignores dynamical information about interventions (e.g., the duration of effects), and extending measurements and models in this direction could augment the signal considerably (Dekker et al., 2021). Such information could then be used to assess these interventions in a more precise fashion.
Not all interventions are amenable to the BECON approach. For instance, certain interventions may be highly effective in controlling the virus spread without implementing large changes in the network. A salient example arises when interventions are directed at interrupting processes that run on specific parts of the contact network, rather than at changing the network structure globally. Such interruptions are, for instance, the goal of contact tracing (Cencetti et al., 2020; Kojaku, Hébert-Dufresne, Mones, Lehmann, & Ahn, 2021; Kretzschmar et al., 2020). Interventions based on contact tracing provide highly local and surgical interventions on the network (namely, by isolating potentially infected cases, such procedures delete the corresponding links from the contact network). It is unlikely that global measures like BECONs would be able to pick up such subtle effects, especially if cases are rare so that relatively few links are deleted. Also, it would be important to study whether contact tracing interventions invariably lead to structures that diminish the potential for virus transmission; one can imagine situations where alarm systems based on contact tracing may instigate behavior that increases virus transmission. This would especially be relevant if alarm systems are unreliable or are activated too late, which underscores the importance of accurate prediction.
In the future, network theory may assist behavioral scientists in developing novel interventions. For example, if advanced reconstruction of the contact network to a high level of precision becomes feasible, interventions could be shaped by the analysis of the baseline network itself. In such an approach, one could first analyze the baseline contact network, and then explicitly design interventions to target particular aspects of the contact network to induce maximal change, analogous to the use of targeted vaccinations in epidemiology (Q. Liu, Zhou, & Van Mieghem, 2019; Pastor-Satorras & Vespignani, 2002). Similarly, interventions could be explicitly targeted to decrease the spectral radius of the contact network (Van Mieghem et al., 2011), because this controls the potential for outbreaks (Van Mieghem & Van de Bovenkamp, 2013; Van Mieghem & van de Bovenkamp, 2015). In accordance, targeted evaluations of changes in the contact network after intervention could be used to assess whether the intended changes have indeed been accomplished. This approach potentially defines an extensive research program, in which behavioral data scientists, epidemiologists, psychologists, computer scientists, and statisticians could profitably work together to construct, implement, and monitor optimal interventions.
Albert, R., Jeong, H., & Barabási, A.-L. (2000). Error and attack tolerance of complex networks. Nature, 406(6794), 378–382. doi: https://doi.org/10.1038/35019019
Backer, J. A., Klinkenberg, D., & Wallinga, J. (2020). Incubation period of 2019 novel coronavirus (2019- nCoV) infections among travellers from Wuhan, China, 20 28 January 2020. Eurosurveillance, 25(5), 1–6. Retrieved from http://dx.doi.org/10.2807/1560-7917.ES.2020.25.5.2000062 doi: https://doi.org/10.2807/1560-7917.ES.2020.25.5.2000062
Blanken, T. F., Tanis, C. C., Nauta, F. H., Dablander, F., Zijlstra, B. J. H., Bouten, R. R. M., … Borsboom, D. (2021). Promoting physical distancing during COVID-19: a systematic approach to compare behavioral interventions. Scientific Reports, 11(1), 19463. Retrieved from https://doi.org/10.1038/s41598-021-98964-z doi: https://doi.org/10.1038/s41598-021-98964-z
Block, P., Hoffman, M., Raabe, I. J., Dowd, J. B., Rahal, C., Kashyap, R., & Mills, M. C. (2020). Social network-based distancing strategies to flatten the covid-19 curve in a post-lockdown world. Nature Human Behaviour, 1–9. doi: https://doi.org/10.1038/s41562-020-0898-6
Carne, C., Semple, S., Morrogh-Bernard, H., Zuberbuehler, K., & Lehmann, J. (2013). Predicting the vulnerability of great apes to disease: the role of superspreaders and their potential vaccination. PLoS One, 8(12), e84642. doi: https://doi.org/10.1371/journal.pone.0084642
CDC. (2020). How COVID-19 spreads. Retrieved 2021-07-14, from https://www.cdc.gov/coronavirus/2019-ncov/prevent-getting-sick/how-covid-spreads.html (Accessed on 28-09-2021)
Cencetti, G., Santin, G., Longa, A., Pigani, E., Barrat, A., Cattuto, C., … Lepri, B. (2020). Using real-world contact networks to quantify the effectiveness of digital contact tracing and isolation strategies for Covid-19 pandemic. medRxiv.
Chu, D. K., Akl, E. A., Duda, S., Solo, K., Yaacoub, S., Schünemann, H. J., … others (2020). Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: a systematic review and meta-analysis. The Lancet, 395(10242), 1973–1987. doi: https://doi.org/10.1016/j.jvs.2020.07.040
Clauset, A., Moore, C., & Newman, M. E. (2008). Hierarchical structure and the prediction of missing links in networks. Nature, 453(7191), 98–101. doi: https://doi.org/10.1038/nature06830
Csardi, G., & Nepusz, T. (2006). The igraph software package for complex network research. InterJournal, Complex Systems, 1695(5), 1–9.
Dekker, M. M., Blanken, T. F., Dablander, F., Ou, J., Borsboom, D., & Panja, D. (2021). Quantifying agent impacts on contact sequences in social interactions. arXiv preprint arXiv:2107.01443. doi: https://doi.org/10.1038/s41598-022-07384-0
Delamater, P. L., Street, E. J., Leslie, T. F., Yang, Y. T., & Jacobsen, K. H. (2019). Complexity of the basic reproduction number ($R_0$). Emerging infectious diseases, 25(1), 1.
de Vlas, S. J., & Coffeng, L. E. (2021). Achieving herd immunity against covid-19 at the country level by the exit strategy of a phased lift of control. Scientific Reports, 11(1), 1–7. doi: https://doi.org/10.1038/s41598-021-83492-7
Drazen, J., Kanapathipillai, R., Campion, E., Rubin, E., Hammer, S., Morrissey, S., & Baden, L. (2014). Ebola and quarantine. The New England Journal of Medicine, 371(21), 2029–2030. doi: https://doi.org/10.1056/nejme1413139
Eyre, D. W., Taylor, D., Purver, M., Chapman, D., Fowler, T., Pouwels, K. B., … Peto, T. E. (2022). Effect of covid-19 vaccination on transmission of alpha and delta variants. New England Journal of Medicine, 386(8), 744-756. Retrieved from https://doi.org/10.1056/NEJMoa2116597 doi: https://doi.org/10.1056/NEJMoa2116597
Ferguson, N., Laydon, D., Nedjati-Gilani, G., Imai, N., Ainslie, K., Baguelin, M., … others (2020). Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID19 mortality and healthcare demand. Imperial College London, 10(77482), 491–497.
Flaxman, S., Mishra, S., Gandy, A., Unwin, H. J. T., Mellan, T. A., Coupland, H., … others (2020). Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature, 584(7820), 257–261. doi: https://doi.org/10.1038/s41586-020-2405-7
Ghasemian, A., Hosseinmardi, H., Galstyan, A., Airoldi, E. M., & Clauset, A. (2020). Stacking models for nearly optimal link prediction in complex networks. Proceedings of the National Academy of Sciences, 117(38), 23393–23400. doi: https://doi.org/10.1073/pnas.1914950117
Goyal, P., & Ferrara, E. (2018). Graph embedding techniques, applications, and performance: A survey. Knowledge-Based Systems, 151, 78–94. doi: https://doi.org/10.1016/j.knosys.2018.03.022
Grimmett, G. (2018). Probability on graphs: random processes on graphs and lattices (Vol. 8). Cambridge University Press. doi: https://doi.org/10.1017/9781108528986
Guimerà, R., & Sales-Pardo, M. (2009). Missing and spurious interactions and the reconstruction of complex networks. Proceedings of the National Academy of Sciences, 106(52), 22073–22078. doi: https://doi.org/10.1073/pnas.0908366106
Heesterbeek, H., Anderson, R. M., Andreasen, V., Bansal, S., De Angelis, D., Dye, C., … others (2015). Modeling infectious disease dynamics in the complex landscape of global health. Science, 347(6227). doi: https://doi.org/10.1126/science.aaa4339
Jeffrey, B., Walters, C. E., Ainslie, K. E., Eales, O., Ciavarella, C., Bhatia, S., … others (2020). Anonymised and aggregated crowd level mobility data from mobile phones suggests that initial compliance with COVID-19 social distancing interventions was high and geographically consistent across the UK. Wellcome Open Research, 5. doi: https://doi.org/10.12688/wellcomeopenres.15997.1
Keeling, M. J., & Rohani, P. (2011). Modeling infectious diseases in humans and animals. Princeton University Press. doi: https://doi.org/10.2307/j.ctvcm4gk0
Kojaku, S., Hébert-Dufresne, L., Mones, E., Lehmann, S., & Ahn, Y.-Y. (2021). The effectiveness of backward contact tracing in networks. Nature Physics, 17(5), 652–658. doi: https://doi.org/10.1038/s41567-021-01187-2
Kretzschmar, M. E., Rozhnova, G., Bootsma, M. C., van Boven, M., van de Wijgert, J. H., & Bonten, M. J. (2020). Impact of delays on effectiveness of contact tracing strategies for COVID-19: a modelling study. The Lancet Public Health, 5(8), e452–e459. doi: https://doi.org/10.1016/s2468-2667(20)30157-2
Liu, Q., Zhou, X., & Van Mieghem, P. (2019). Pulse strategy for suppressing spreading on networks. Europhysics Letters, 127(3), 38001. doi: https://doi.org/10.1209/0295-5075/127/38001
Liu, Y., Sanhedrai, H., Dong, G., Shekhtman, L. M., Wang, F., Buldyrev, S. V., & Havlin, S. (2021). Efficient network immunization under limited knowledge. National Science Review, 8(1), nwaa229.
Meredith, W. (1993). Measurement invariance, factor analysis and factorial invariance. Psychometrika, 58(4), 525–543. doi: https://doi.org/10.1007/bf02294825
Newman, M. (2018). Networks. Oxford university press. doi: https://doi.org/10.1093/oso/9780198805090.001.0001
Pastor-Satorras, R., Castellano, C., Van Mieghem, P., & Vespignani, A. (2015). Epidemic processes in complex networks. Reviews of Modern Physics, 87(3), 925–979. doi: https://doi.org/10.1103/revmodphys.87.925
Pastor-Satorras, R., & Vespignani, A. (2002). Immunization of complex networks. Physical review E, 65(3), 036104. doi: https://doi.org/10.1103/physreve.65.036104
Rushmore, J., Caillaud, D., Hall, R. J., Stumpf, R. M., Meyers, L. A., & Altizer, S. (2014). Network-based vaccination improves prospects for disease control in wild chimpanzees. Journal of the Royal Society Interface, 11(97), 20140349. doi: https://doi.org/10.1098/rsif.2014.0349
Sahneh, F. D., Scoglio, C., & Van Mieghem, P. (2013). Generalized epidemic mean-field model for spreading processes over multilayer complex networks. IEEE/ACM Transactions on Networking, 21(5), 1609–1620. doi: https://doi.org/10.1109/tnet.2013.2239658
Tanis, C. C., Leach, N. M., Geiger, S. J., Nauta, F. H., Dablander, F., Harreveld, F. v., … Blanken, T. F. (2021). Smart Distance Lab’s art fair, experimental data on social distancing during the COVID-19 pandemic. Scientific Data, 8, 179. doi: https://doi.org/https://doi.org/10.1038/s41597-021-00971-2
Trajanovski, S., Martín-Hernández, J., Winterbach, W., & Van Mieghem, P. (2013). Robustness envelopes of networks. Journal of Complex Networks, 1(1), 44–62. doi: https://doi.org/10.1093/comnet/cnt004
Trofimenko, T. B., Mukhina, K. D., & Visheratin, A. A. (2016). Mobile contacts network reconstruction using call domain records data. In 2016 third european network intelligence conference (enic) (pp. 55–60). doi: https://doi.org/10.1109/enic.2016.016
Van De Schoot, R., Kluytmans, A., Tummers, L., Lugtig, P., Hox, J., & Muthén, B. (2013). Facing off with Scylla and Charybdis: a comparison of scalar, partial, and the novel possibility of approximate measurement invariance. Frontiers in Psychology, 4, 770. doi: https://doi.org/10.3389/fpsyg.2013.00770
Van Mieghem, P. (2014). Performance analysis of complex networks and systems. Cambridge University Press.
Van Mieghem, P., Stevanović, D., Kuipers, F., Li, C., Van De Bovenkamp, R., Liu, D., & Wang, H. (2011). Decreasing the spectral radius of a graph by link removals. Physical Review E, 84(1), 016101. doi: https://doi.org/10.1103/physreve.84.016101
Van Mieghem, P., & Van de Bovenkamp, R. (2013). Non-Markovian infection spread dramatically alters the susceptible-infected-susceptible epidemic threshold in networks. Physical review letters, 110(10), 108701. doi: https://doi.org/10.1103/physrevlett.110.108701
Van Mieghem, P., & van de Bovenkamp, R. (2015). Accuracy criterion for the mean-field approximation in susceptible-infected-susceptible epidemics on networks. Physical Review E, 91(3), 032812. doi: https://doi.org/10.1103/physreve.91.032812
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of ‘small-world’networks. Nature, 393(6684), 440–442. doi: https://doi.org/10.1515/9781400841356.301
Additional tables and figures reporting the simulation results across all conditions. Complete results are available at https://gitlab.com/science-versus-corona/becon.
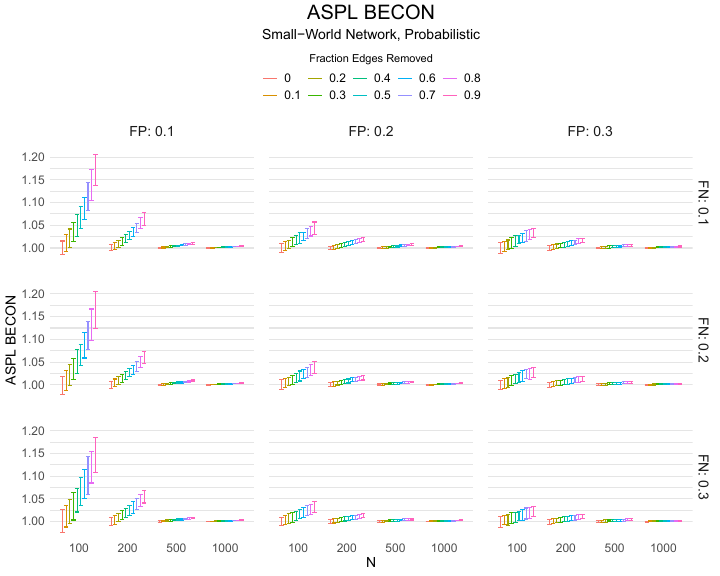
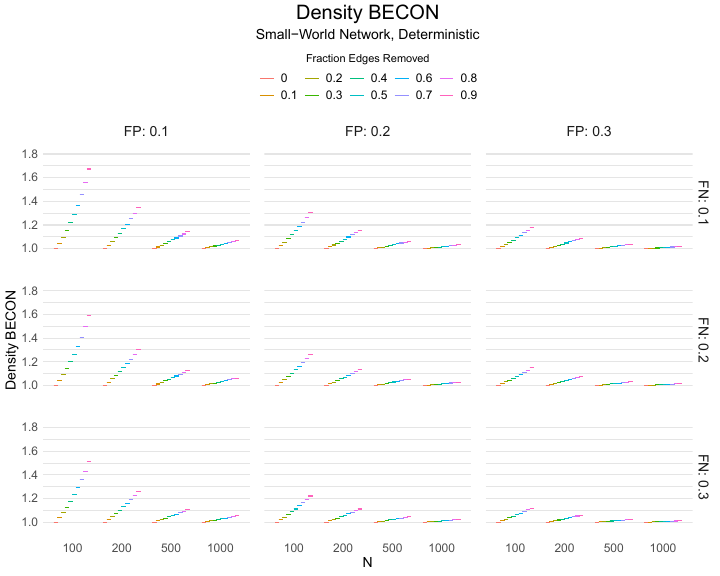
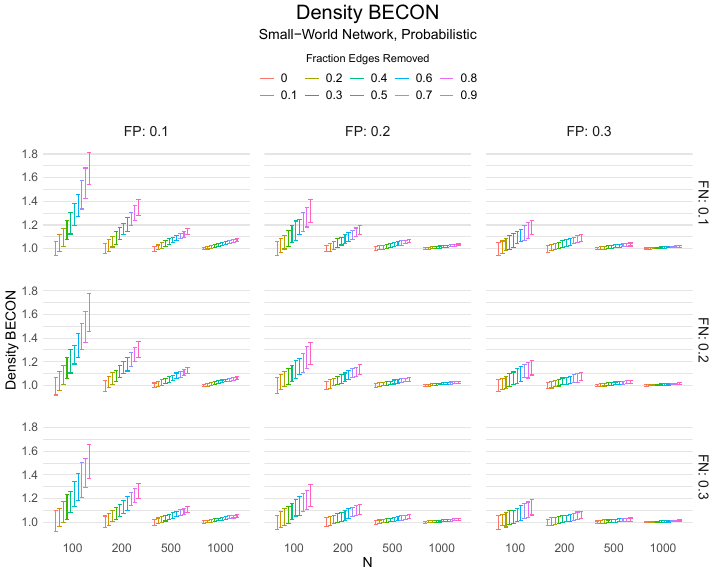
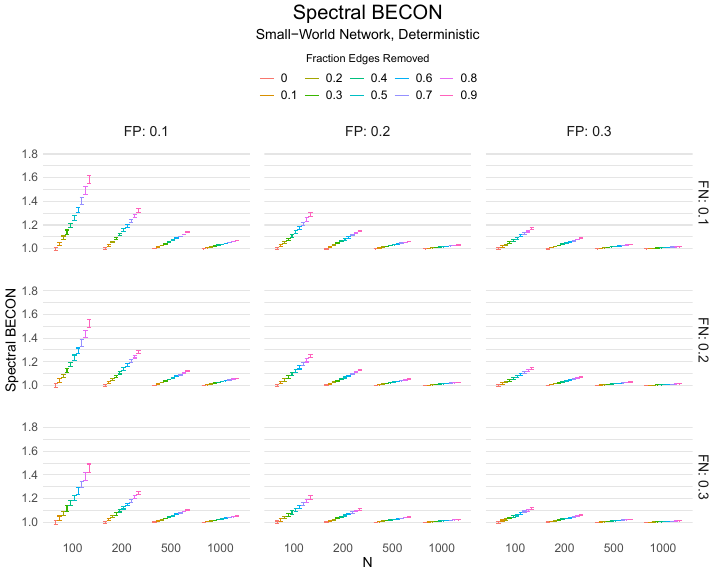
| $n$ | FP | Deterministic | Probabilistic
| |||||||||||
Density | Spectral | ASPL | Density | Spectral | ASPL
| |||||||||
| $r$ | $SD$ | $r$ | $SD$ | $r$ | $SD$ | $r$ | $SD$ | $r$ | $SD$ | $r$ | $SD$ | |||
| 100 | 0.1 | 1 | 0 | 1 | 0 | 1 | 0 | 0.97 | 0.02 | 0.98 | 0.02 | 0.97 | 0.02 | |
| 100 | 0.2 | 1 | 0 | 1 | 0 | 1 | 0 | 0.92 | 0.06 | 0.93 | 0.06 | 0.92 | 0.07 | |
| 100 | 0.3 | 1 | 0 | 1 | 0 | 1 | 0 | 0.86 | 0.1 | 0.87 | 0.1 | 0.85 | 0.1 | |
| 200 | 0.1 | 1 | 0 | 1 | 0 | 1 | 0 | 0.97 | 0.03 | 0.98 | 0.02 | 0.97 | 0.03 | |
| 200 | 0.2 | 1 | 0 | 1 | 0 | 1 | 0 | 0.92 | 0.06 | 0.93 | 0.06 | 0.91 | 0.06 | |
| 200 | 0.3 | 1 | 0 | 1 | 0 | 1 | 0 | 0.85 | 0.1 | 0.86 | 0.1 | 0.84 | 0.11 | |
| 500 | 0.1 | 1 | 0 | 1 | 0 | 1 | 0 | 0.97 | 0.03 | 0.97 | 0.02 | 0.97 | 0.03 | |
| 500 | 0.2 | 1 | 0 | 1 | 0 | 1 | 0 | 0.92 | 0.06 | 0.92 | 0.05 | 0.92 | 0.06 | |
| 500 | 0.3 | 1 | 0 | 1 | 0 | 1 | 0 | 0.86 | 0.1 | 0.86 | 0.09 | 0.86 | 0.1 | |
| 1000 | 0.1 | 1 | 0 | 1 | 0 | 1 | 0 | 0.97 | 0.03 | 0.97 | 0.02 | 0.97 | 0.03 | |
| 1000 | 0.2 | 1 | 0 | 1 | 0 | 1 | 0 | 0.92 | 0.06 | 0.92 | 0.05 | 0.92 | 0.06 | |
| 1000 | 0.3 | 1 | 0 | 1 | 0 | 1 | 0 | 0.86 | 0.1 | 0.86 | 0.1 | 0.86 | 0.1 | |
| $n$ | FP | Deterministic | Probabilistic
| |||||||||||
Density | Spectral | ASPL | Density | Spectral | ASPL
| |||||||||
| $r$ | $SD$ | $r$ | $SD$ | $r$ | $SD$ | $r$ | $SD$ | $r$ | $SD$ | $r$ | $SD$ | |||
| 100 | 0.1 | 1 | 0 | 1 | 0 | 1 | 0 | 0.97 | 0.02 | 0.97 | 0.02 | 0.97 | 0.02 | |
| 100 | 0.2 | 1 | 0 | 1 | 0 | 1 | 0 | 0.92 | 0.06 | 0.92 | 0.06 | 0.92 | 0.06 | |
| 100 | 0.3 | 1 | 0 | 1 | 0 | 1 | 0 | 0.85 | 0.11 | 0.85 | 0.11 | 0.84 | 0.11 | |
| 200 | 0.1 | 1 | 0 | 1 | 0 | 1 | 0 | 0.97 | 0.02 | 0.97 | 0.03 | 0.97 | 0.02 | |
| 200 | 0.2 | 1 | 0 | 1 | 0 | 1 | 0 | 0.92 | 0.05 | 0.92 | 0.05 | 0.92 | 0.06 | |
| 200 | 0.3 | 1 | 0 | 1 | 0 | 1 | 0 | 0.85 | 0.09 | 0.85 | 0.1 | 0.85 | 0.09 | |
| 500 | 0.1 | 1 | 0 | 1 | 0 | 1 | 0 | 0.97 | 0.03 | 0.97 | 0.03 | 0.97 | 0.03 | |
| 500 | 0.2 | 1 | 0 | 1 | 0 | 1 | 0 | 0.92 | 0.06 | 0.92 | 0.06 | 0.92 | 0.06 | |
| 500 | 0.3 | 1 | 0 | 1 | 0 | 1 | 0 | 0.85 | 0.1 | 0.85 | 0.1 | 0.85 | 0.1 | |
| 1000 | 0.1 | 1 | 0 | 1 | 0 | 1 | 0 | 0.97 | 0.03 | 0.97 | 0.03 | 0.96 | 0.03 | |
| 1000 | 0.2 | 1 | 0 | 1 | 0 | 1 | 0 | 0.91 | 0.06 | 0.91 | 0.06 | 0.91 | 0.06 | |
| 1000 | 0.3 | 1 | 0 | 1 | 0 | 1 | 0 | 0.85 | 0.11 | 0.85 | 0.11 | 0.85 | 0.11 | |
3 Here it is important to note that for COVID-19, vaccination does not preclude an individual from receiving or spreading the virus, although transmission rates among vaccinated individuals were reduced. (Eyre et al., 2022)