Keywords: Piecewise Growth Curve Models · Bayesian SEM · Model Selection
Developmental researchers often study within-person change over time to better understand a variety of dynamic processes. For example, Marks and Coll (2007) contrasted growth in reading and math skills in children across four major ethnic groups from kindergarten through third grade in order to highlight the needs of American Indian and Alaska Native youth. Seider et al. (2019) documented the development of Black and Latino high school students’ beliefs about poverty and racism to examine the role of schooling and how these beliefs relate to each other. Finally, Shono, Edwards, Ames, and Stacy (2018) captured change in cannabis use across teen years as a component of validity testing a new cannabis-related word association test. These examples highlight a wide range of topics within developmental research.
For many developmental research questions, choosing an appropriate model to summarize the trajectory of development over time is crucial. Longitudinal methods typically describe within-person change and explain between-person differences in that change. There are many longitudinal models available, and a truly helpful model will guide the researcher to evaluate their research questions and meaningfully communicate their findings. Of the many different model forms that researchers can choose from, the growth curve model (GCM) is perhaps one of the more beneficial for tracking change over multiple time-points. The GCM uses repeated observations to estimate the latent population trajectory. Through GCMs, researchers can summarize change over time or test hypotheses about specific aspects of growth (e.g., the rate of change). In addition to summarizing within-person change, GCMs also allow researchers to examine between-person variability in development.
The GCM has many forms, and the simplest captures linear change over time (called a “linear GCM”). Researchers using a linear GCM can describe change with growth parameters that are straightforward to interpret: a mean intercept and a mean slope. For example, Marks and Coll (2007) examined differences in reading development by interpreting the initial level of reading (i.e., the intercept) and the average rate of change (i.e., the slope) across ethnic groups. The linear GCM is useful in many research scenarios, but it also has some limitations that applied researchers should consider while selecting a model. The main limitation is that it assumes the true growth trajectory is a straight line, and can not capture nonlinear changes that may be of substantive importance.
In some cases examining more dynamic processes, this linear assumption is too restrictive and will not capture the substantive changes of most interest. Development may follow a curve or other irregular deviations from linearity. For example, Zimmer-Gembeck et al. (2021) found the development of social anxiety in adolescents was best represented by a quadratic GCM. Vargas Lascano, Galambos, Krahn, and Lachman (2015) found that a cubic model best fit the shifts in perceived control in adults aged 18 to 43. In aging adults across the last 16 years of life, Schillin, Deeg, and Huisman (2018) found that the decrease in positive affect was best captured by an exponential GCM. The developmental trajectories in these studies were not linear, and so the researchers used GCMs that assumed a nonlinear growth trajectory.
An alternative to imposing any assumptions about the shape of the overall trajectory (e.g., a quadratic growth model) is to instead capture the trajectory with several linear segments using a linear piecewise growth curve model (PGCM; Meredith & Tisak, 1990). The word “piecewise” indicates that the linear slope may be different across different “pieces” of the study period, which gives the researcher greater flexibility while maintaining simple parameters. For example, Finkel, Reynolds, McArdle, and Gatz (2003) used a linear PGCM to capture cognitive decline in adults over 60 years of age, estimating different rates of change for observations before and after age 65. This approach allowed them to show that aging adults under 65 improved each year on certain cognitive measures, but those scores declined after age 65. More recently, Gaudreau, Louvet, and Kljajic (2018) used a piecewise approach to capture the development of adolescents’ performance in gymnastics classes, which decreased for the first three classes before showing consistent improvement in the last three classes of the study period. Taking a piecewise approach allowed these researchers to capture unique shifts in the direction of development over time.
These researchers used the simplest piecewise model: a linear-linear PGCM. This type of PGCM is useful for capturing a nonlinear trajectory with a single change in direction such as the switch from declining to improving performance in gymnastics (as shown in Gaudreau et al., 2018). A linear-linear PGCM uses two phases of growth, but PGCMs with additional phases are possible with enough measurement occasions. For growth trajectories with more complex nonlinearity (i.e., growth with more than one change in direction), researchers may wish to use additional phases. In the frequentist framework, the number of phases is somewhat restricted in order to maintain model identification. One way to work around this restriction is to estimate PGCMs in the Bayesian estimation framework, an alternative approach that can be used to estimate some non-identified models. For PGCMs, this allows additional phases of growth.
In addition to allowing more phases of growth in PGCMs, Bayesian estimation has been shown to handle complex models with fewer estimation issues (e.g., convergence, biased estimates). Instead of relying solely on observed data and a likelihood function, Bayesian methods also incorporate prior information into estimation using a prior distribution. Wang and McArdle (2008) found that Bayesian estimation fairly accurately captures parameters in nonlinear piecewise growth models, and Depaoli (2013) found that Bayesian growth mixture models estimated using informative priors yielded minimal bias in parameter estimates. Using Bayesian estimation methods with thoughtfully selected prior distributions can help to accurately recover model parameters.
Bayesian PGCMs extend conventionally-taught linear growth models by altering both the functional form of growth and the estimation framework. This is an active area of methodological development, with recent extensions that enable the direct estimation of knot placement (Kohli, Hughes, Wang, Zopluoglu, & Davison, 2015; Lock, Kohli, & Bose, 2018), incorporation of covariates (Lamm, 2022), and capturing the interdependent nature of bivariate piecewise trajectories (Peralta, Kohli, Lock, & Davison, 2022). Our intended scope for the current paper is to provide an introductory, hands-on walkthrough to the novice data scientist or graduate student. That is, our tutorial is written to bridge the knowledge gap between linear growth curve models in the frequentist framework and more complex piecewise models estimated in the Bayesian framework. Given this audience, the specific goals of the current paper are:
Present readers to Bayesian PGCMs as a flexible way to capture complex nonlinearity.
Thoroughly illustrate Bayesian PGCMs with an empirical dataset, including how to select priors.
Provide readers with additional resources to expand on this tutorial.
To achieve these goals, the remaining sections of the paper are structured as follows. First, we describe linear GCMs and how linear PGCMs are a simple extension. We also highlight how to extend PGCMs beyond two phases of growth. Second, we introduce Bayesian estimation. Our explanation describes some benefits of Bayesian estimation, key terminology, how to specify priors, and how the Bayesian framework allows additional phases of growth. Third, we present an illustration of Bayesian PGCMs applied to nonlinear growth in childrens’ math achievement. This demonstration provides the syntax to implement the model in Mplus, illustrates how to use comparative model indices to select the best model, and shows how to interpret model results. Finally, we discuss the limitations of linear PGCMs and possible extensions.
The main goal of a growth model is to summarize many repeated within-person observations with a few growth parameters. The general form of a growth model is \begin {equation} \label {generic_growth} y_{j} = g(t_{j}) + e_{j}, \end {equation} which says that the \(j\)th measurement of the variable \(y\) is the sum of some function of time at the \(j\)th measurement \(g(t_{j})\) and timing-specific measurement error \(e_{j}\). The \(j\) subscript indicates that the outcome, time, and error can vary across all \(j=1,2,...,J\) measurement occasions. In the following sections, we describe different specifications of \(g(t_{j})\). Next we describe a linear GCM, how GCMs can be adapted for nonlinearity, a two-phase linear PGCM, and linear PGCMs with three or more phases. Finally, we connect these models to Mplus syntax.
A linear GCM assumes the growth function \(g(t_j)\) is a linear function of time t: \begin {equation} \label {linear_growth_mean} g(t_j) = \beta _0 + \beta _1t_j, \end {equation} where \(\beta _0\) represents the intercept and \(\beta _1\) represents the expected rate of change for every \(1\)-unit increase in time \(t_j\)1 . We refer to these coefficients as growth parameters. Researchers are typically interested in estimating linear growth parameters using a sample of \(i=1,2,...,N\) persons with repeated measurements at \(J\) different time points. To clarify that we are interested in estimating person-specific outcomes as a function of person-specific time, we add an \(i\) subscript to \(g(t_{j})\) in Equation (2). The linear growth function can be given by \begin {equation} g(t_{ij}) = \beta _{0} + \beta _1t_{ij}, \end {equation} where the growth function of person \(i\)’s time at measurement occasion \(j\) is a linear function with intercept \(\beta _0\) and slope \(\beta _1\). Plugging in this growth function and adding an \(i\) subscript to Equation (1) gives \begin {equation} \label {constrained_linear_growth} y_{ij} = \beta _0 + \beta _1t_{ij} + e_{ij}, \end {equation} where \(y_{ij}\) refers to the outcome variable for person \(i\) at time \(j\), \(t_{ij}\) is person \(i\)’s time measured at time point \(j\), and \(e_{ij}\) is unexplained error for person \(i\) at time point \(j\). We assume that \(e_{ij}\) is normally distributed around zero, or \(e_{ij} \sim N(0, \sigma ^2_{ej})\). The error variance parameter \(\sigma ^2_{ej}\) represents variability in the observed data at time \(j\) that is unexplained by the model. The two coefficients in this model, \(\beta _0\) and \(\beta _1\), refer to growth parameters that are held constant across persons. However, there is often some between-person fluctuations in the growth parameters. Imposing the same intercept and slope on each participant in the sample can lead to higher measurement error \(e_{ij}\). To prevent this, we introduce a person-specific growth function, \(d_i(t_{ij})\). We define \(d_i(t_{ij})\) as, \begin {equation} \label {linear_growth_d_i} d_i(t_{ij}) = \delta _{0i} + \delta _{1i}t_{ij}, \end {equation} where \(\delta _{0i}\) and \(\delta _{1i}\) refer to a person-specific intercept and slope, respectively. We assume the values of \(\delta _{0i}\) are distributed normally with a mean of \(\beta _0\) and that \(\delta _{1i}\) is normally distributed around \(\beta _1\). These assumptions can be summarized in the following way: \begin {equation} \label {delta_distribution} \begin {bmatrix}\delta _0\\ \delta _1 \end {bmatrix} \sim MVN\left ( \begin {bmatrix}\beta _0\\ \beta _1 \end {bmatrix}, \mathbf {\Sigma _{\delta }} \right ), \end {equation} where \(\mathbf {\Sigma _{\delta }}\) is a \(2\times 2\) covariance matrix. The diagonal elements of this matrix describe the variance of the intercept and variance of the slope. The off-diagonal element describes the covariance of the intercept and slope. These variances can have interesting substantive meaning. For example, if a researcher studied the number of words children learn from age two to five and found the variance of the intercept is smaller than the variance of the slope, this suggests that the number of words children knew at age two varies less than how many new words children learned per year. By replacing \(g(t_{j})\) with \(d_i(t_{ij})\) in Equation (1), we can write the full linear GCM, \begin {equation} \label {linear_growth_y} y_{ij} = \delta _{0i} + \delta _{1i}t_{ij} + e_{ij}, \end {equation} which describes the outcome variable \(y_{ij}\) as a function of time \(t_{ij}\) and person \(i\)’s growth parameters \(\delta _{0i}\) and \(\delta _{1i}\).
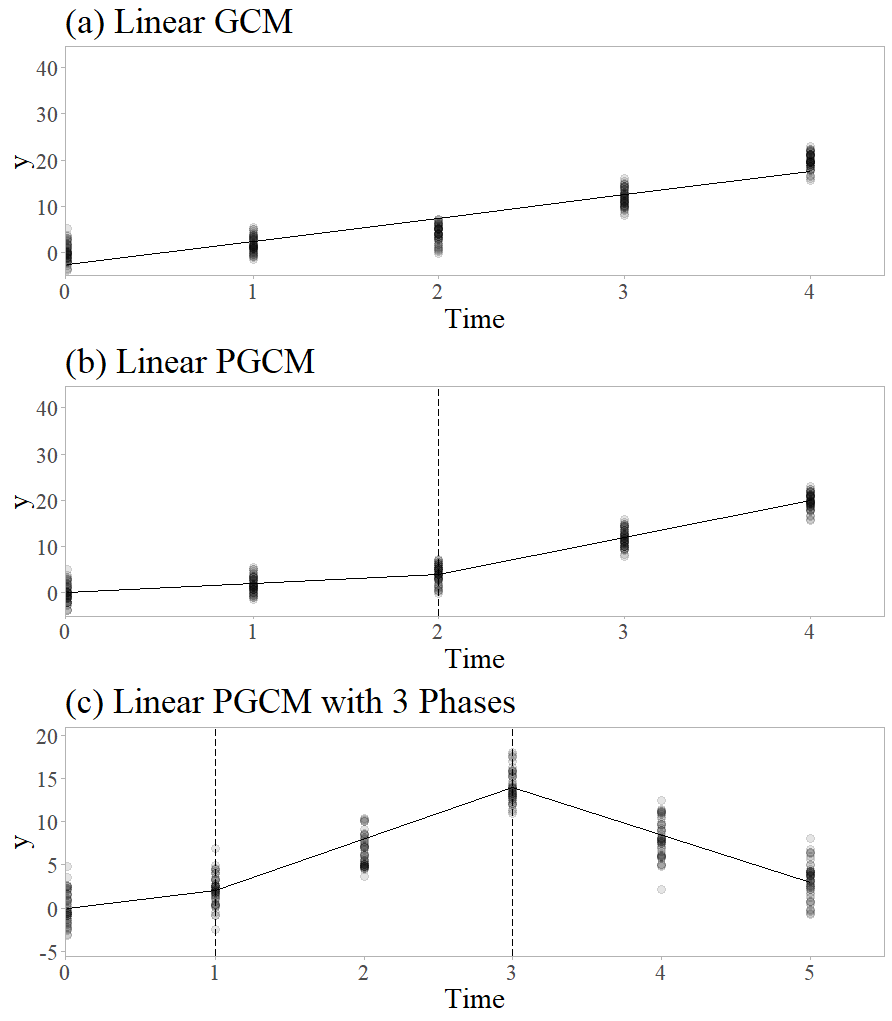
Linear GCMs assume change over time can be captured with a straight line, but in some cases this linear assumption is too restrictive. Change in a variable over time may follow a curve or have other deviations from linear change. When change is not linear, the researcher’s analysis plan must transition to capture nonlinearity. There are many ways to model nonlinearity, but these extensions may have limited applicability. For example, a researcher may add a third term such as “\(+\delta _{2i}t^2_{ij}\)” to Equation (7) to estimate a quadratic coefficient \(\delta _{2i}\) for trajectories shaped like a parabola. Researchers can also alter linear GCM specifications in more complex ways to capture cyclical growth with a sine function (e.g. Bollen & Curran, 2006) or S-shaped growth with a Gompertz curve (e.g. Grimm & Ram, 2009). The parameters estimated by these models are shape-specific and some may be challenging to substantively interpret. When the goal of the model is simply to capture the trajectory, this is not a problem. However, when the researcher wants a simpler interpretation of growth parameters, an alternative method is to break up the trajectory into linear phases as shown in Figure 1. These phases comprise a “piecewise” approach to modeling nonlinear growth patterns. Using this piecewise approach allows a GCM to capture nonlinear growth while maintaining the simple interpretation of linear slope parameters.
The simplest piecewise model uses two phases to capture growth with a single change in direction. The time when one growth phase switches to another is called a knot, denoted \(k\). The knot is placed at a measurement occasion chosen by the researcher. We adapt the growth function in Equation (5) to include a change in slope at \(k\): \begin {equation} \label {d_i_single_knot} d_i(t_{ij}) = \delta _{0i} + \delta _{1i}t_{ij} + \delta _{2i}(t_{ij}-k)_+. \end {equation} Here, \(\delta _{2i}\) represents the person-specific change in slope that occurs at values of \(t_{ij}\) after the knot. Similar to the other coefficients, \(\delta _{2i}\) has a mean of \(\beta _2\) and information about its variance and covariances are contained in a \(3\times 3\) covariance matrix \(\mathbf {\Sigma _{\delta }}\). To implement a change in slope for some values of \(t_{ij}\) but not others, we introduce a new term, \((t_{ij} - k)_+\), which represents “the positive part of \(t_{ij}-k\)”. This is defined as,
\begin {equation} \label {positive_part} (t_{ij} - k)_+ = \begin {cases} 0 &\text {if $t_{ij} \leq k$}\\ t_{ij} - k &\text {if $t_{ij} > k$},\\ \end {cases} \end {equation} which means the term \((t_{ij}-k)_+\) only appears when \(t_{ij} - k\) positive. This means in Equation (8), person \(i\)’s linear slope when \(t \leq k\) is \(\delta _{1i}\), but the slope for \(t > k\) is \(\delta _{1i} + \delta _{2i}\). Adding this to Equation (7) gives the linear PGCM with one knot: \begin {equation} \label {y_single_knot} y_{ij} = \delta _{0i} + \delta _{1i}t_{ij} + \delta _{2i}(t_{ij}-k)_+ + e_{ij}. \end {equation} Here, the coefficients \(\delta _{0i}\) and \(\delta _{1i}\) describe person-specific growth parameters in the first phase of growth. The person-specific change in slope at \(k\) is described by \(\delta _{2i}\). The last term, \(e_{ij}\), describes leftover error that is not captured by \(d_i(t_{ij})\). To illustrate this, consider Figure 1, which shows a linear GCM in part (a) and a linear PGCM in part (b). In part (b), there are four measurement occasions \(t_1=0\), \(t_2=1\), \(t_3=2\), and \(t_4=3\), and a knot, \(k=2\). The rate of growth increases at the knot, which appears visually as a steeper slope from \(k=2\) onward.

In the frequentist framework, extending piecewise models beyond two phases of growth requires several measurement occasions. For example, Bollen and Curran (2006) showed at least five measurement occasions are required to estimate a two-phase PGCM, and Flora (2008) noted that a three-phase PGCM needs at least seven measurements. These restrictions ensure the model is identified, meaning it has enough observed variables to estimate the parameters. A non-identified model cannot be estimated using frequentist methods. In this section we describe PGCMs with three or more phases, which traditionally require many measurement occasions. Later we describe the Bayesian estimation framework, an alternative approach that can estimate non-identified models.
To create more phases, the researcher must specify more knots. To refer to \(M\) specific knots, we use \(k_1, k_2, ..., k_M\). First, we generalize the person-specific growth function \(d_i(t_{ij})\) to address more phases of growth: \begin {equation} \label {d_i_multiple_knots} d_i(t_{ij}) = \delta _{0i} + \delta _{1i}t_{ij} + \sum ^M_{m=1}\delta _{(1+m)i}(t_{ij}-k_m)_+. \end {equation} The change from \(\delta _{2i}\) in Equation (8) to \(\sum ^M_{m=1}\delta _{(1+m)i}\) here generalizes the growth function to handle more than two phases. Each coefficient next to the summation sign \(\delta _{2i}, \delta _{3i},...,\delta _{(1+M)i}\) refers to a change in slope that occurs after the first phase. For example, for a model with \(M=5\) knots, the slope in the sixth and final phase of growth would be \(\delta _{1i} + \delta _{2i} +...+\delta _{6i}\), or \(\delta _{1i} + \sum ^5_{m=1}\delta _{(1+m)i}\). Putting the growth function from Equation (11) into Equation (1), we get the full linear PGCM: \begin {equation} \label {y_multiple_knots} y_{ij} = \delta _{0i} + \delta _{1i}t_{ij} + \sum ^M_{m=1}\delta _{(1+m)i}(t_{ij}-k_m)_+ + e_{ij}. \end {equation} This model is a generalization of the model shown in Equation (10) that can address two or more phases. The summation describes how the linear slope of each phase of growth is the sum of multiple coefficients.
To illustrate this concept, see part (c) in Figure 1. This plot shows change over six measurements with two knots placed at \(k_1 = 1\) and \(k_2 = 3\). Visually, growth appears slow in the first phase, accelerates in the second phase, then switches to a decline in the third phase. We could specify these knots in Equation (12) in the following way: \begin {equation} \label {example_pgcm} y_{ij} = \delta _{0i} + \delta _{1i}t_{ij} + \delta _{2i}(t_{ij}-1)_+ + \delta _{3i}(t_{ij}-3)_+ + e_{ij}. \end {equation} In this model, the general term \(\sum ^M_{m=1}\delta _{(1+m)i}(t_{ij}-k_m)_+\) has been spelled out as \(\delta _{2i}(t_{ij}-1)_+ + \delta _{3i}(t_{ij}-3)_+\). As before, \(\delta _{0i}\) and \(\delta _{1i}\) describe person i’s growth trajectory in the first phase of growth, which covers \(t_1 = 0\) and \(t_2 = 1\). The second phase of growth extends from the second time point to the fourth, or \(1 < t \leq 3\). The rate of change in this phase is \(\delta _{1i} + \delta _{2i}\). The third phase starts at the second knot \(k_2=3\) and includes the next two time points. This phase of growth has the slope \(\delta _{1i} + \delta _{2i} + \delta _{3i}\). This is equivalent to \(\delta _{1i} + \sum ^2_{m=1}\delta _{(1+m)i}\).
Nonlinear trajectories may show complex nonlinearity that does not have clear phases of growth. In these cases it is not clear how many phases are needed to capture the trend, or where knots should be placed. There may be multiple knot specifications that could capture the trajectory, or developmental theories may disagree on when one phase of growth ends and another begins. In these situations, a model selection approach can be useful.
Model selection is a method where multiple candidate models are estimated and compared before selecting the “best” one. The criteria for this selection is usually one or more model comparison indices, which are often provided by statistical software. These indices may include model fit indices or model comparison indices. Model fit refers to how well an estimated model minimizes error variance or “fits” the data. Model fit indices are used to evaluate the estimated model on some index-specific scale. For example, values below 0.05 suggest excellent fit according to the root mean square error of approximation (RMSEA; Browne & Cudeck, 1992; Steiger & Lind, 1980). Other model fit indices include the Comparative Fit Index (CFI; Bentler, 1990) and Tucker-Lewis Index (TLI; Tucker & Lewis, 1973). In contrast, model comparison is the task of comparing two or more models and selecting the model with the best balance of fit and parsimony.
Model comparison indices may be applied to PGCMs to select the best knot specification out of several candidate models. Two commonly-used indices are the Akaike information criterion (AIC; Akaike, 1992) and the Bayesian information criterion (BIC; Schwarz, 1978). These comparison indices describe the fit of a model (measured using the loglikelihood) penalized by model complexity (the number of free parameters in the model). When evaluating candidate models, the model with the smallest AIC (or BIC) is considered the winning model. For further information on these and other model comparison indices, we refer the reader to Nylund, Asparouhov, and Muthén (2007).
Translating linear PGCMs to syntax is relatively straightforward. We start by showing how to implement the linear model in Equation (7) and part (a) of Figure 1 in Mplus. In this example, the five variables labelled y1, y2, y3, y4, and y5 refer to observations of our variable of interest at five different measurement occasions:
MODEL: delta_0 delta_1 | y1@0 y2@1 y3@2 y4@3 y5@4;
The MODEL command indicates to Mplus that the following lines of code define our model. In the next line, delta_0 and delta_1 refer to the growth parameters we want to estimate: \(\delta _{0i}\) and \(\delta _{1i}\) from Equation (7). The | symbol means the intercept and slope on the left should be estimated using the information on the right. On the right side of the vertical line, we see five main elements. Each of these elements contains a y, an @, and a number. Each observation of \(y\) is paired with a value of \(t\) (represented by the number for each element). The @ symbol means that the value of \(y\) occurred at a specific time \(t\). For example, y1@0 indicates that the first measurement occasion y1 occurred when \(t=0\), which places the intercept at the beginning of the study period. We extend this syntax to address two phases of growth by adding a third line to estimate the change in slope \(\delta _{2i}\) in Equation (10). We can implement the piecewise model in Figure 1 part (b), which uses a single knot \(k=2\), in the following way:
MODEL: delta_0 delta_1 | y1@0 y2@1 y3@2 y4@3 y5@4; delta_0 delta_2 | y1@0 y2@0 y3@0 y4@1 y5@2;
The third line of syntax tells Mplus to estimate a change in slope called delta_2 by pairing each observation of \(y\) with the value of \((t_j - k)_+\). The delta_0 term is included to tell Mplus the growth segments are connected, but it does not mean delta_0 is the intercept of the second segment. As noted in Equation (9), the value of \((t_j - k)_+\) is zero when \(t_j \leq k\). As shown in part (b) Figure 1, the first three observations are left of or equal to the knot at \(k=2\), represented as a dotted line in part (b) of Figure 1. Piecewise models like the one shown in part (c) of Figure 1 are also possible with additional lines of syntax, and we present examples in the Tutorial section.
There are multiple reasons for researchers use the Bayesian estimation framework. Bayesian methods allow researchers to incorporate background knowledge in analyses and use an estimator that does not rely on large sample theory. These features allow Bayesian methods to estimate non-identified models, which may allow the researcher to implement more phases of growth than what is possible in the frequentist framework. Bayesian estimation can also improve the accuracy of parameter estimates in nonlinear growth models (e.g., Depaoli, 2013; Wang & McArdle, 2008). We introduce researchers to the Bayesian estimation framework here by discussing key Bayesian terminology, prior specification, the estimation process, and Bayesian model indices for model selection and evaluation. For more information, we recommend Kruschke (2014) and Depaoli (2021).
Bayesian estimation addresses uncertainty about exact parameter values by treating model parameters as random variables with their own probability distributions. The results of a Bayesian analysis include an estimated probability distribution for each parameter called a posterior distribution. To obtain posterior distributions, the researcher must provide probability distributions called prior distributions, or priors. These priors represent the researcher’s background knowledge about the model parameters. The prior distributions are combined with a likelihood function built from the observed data. The general process of Bayesian estimation in developmental research is to specify our background knowledge of change over time (priors), combine this knowledge with new data, and create an updated description of change over time (posterior distributions).
The prior is a hugely important component of Bayesian estimation that can provide the researcher with potential influence over final parameter estimates. Prior specification is a process where each parameter in the researcher’s model is assigned a probability distribution. Priors may provide more or less information depending on specification. Diffuse priors incorporate uncertainty into the analysis by providing almost no information. In contrast, an informative prior incorporates certainty into the analysis by providing information about likely values for the model parameter.
The level of informativeness of a prior reflects the level of certainty about possible values of the model parameter. As an example, consider the two-phase PGCM shown in Figure 1, part (b) and described in Equation (10). The main parameters in this model are the mean intercept and slope for the first phase, \(\beta _0\) and \(\beta _1\), and the average change in slope in the second phase, \(\beta _2\). These are mean parameters, which are commonly assigned normal distribution priors. Normal distributions are defined by a mean and a standard deviation. One way to assign a prior to \(\beta _0\) is to give it a normal prior with a mean of zero and an extremely large standard deviation such as \(\sigma = 10^{5}\). We write this formally as \(\beta _0 \sim N(0, \sigma = 10^{5})\). This suggests a tremendous range of values, including those as extreme as 1,000,000, are all potential values of \(\beta _0\). This prior is a “diffuse” prior, meaning it does not provide much information about what values of \(\beta _0\) are likely. Alternatively, the researcher may believe \(\beta _0\) lies somewhere between zero and 100. To narrow the range of likely values of \(\beta _0\), the researcher could specify \(\beta _0 \sim N(50, \sigma =20)\). The density of this normal distribution is almost entirely between zero and 100, with values close to 50 more likely than values far away. A similar strategy may be used to assign priors to \(\beta _1\) and \(\beta _2\).
The remaining parameters in the model are the coefficient covariance matrix \(\mathbf {\Sigma _{\delta }}\) and measurement error variances \(\sigma ^2_{e1}, ..., \sigma ^2_{e7}\). Variance parameters should not receive normal priors. In Mplus, the options for variance prior distributions are the inverse gamma distribution or the inverse Wishart distribution. We use the diffuse Mplus default variance priors (described in detail in the tutorial) to focus our demonstration on mean growth parameters, but interested readers can see Asparouhov and Muthén (2021b) for guidance on how to construct informative variance priors.
Careful prior specification is always important in Bayesian estimation, but it is especially crucial for PGCMs with many phases. In the frequentist framework, models must be identified to be estimated. In PGCMs specifically, the requirements for model identification restrict the number of growth phases (Bollen & Curran, 2006; Flora, 2008). The Bayesian estimation framework offers an alternative to the limitations of model identification. Bayesian estimation of non-identified models (e.g., many phases of growth in piecewise growth curve models) are possible because the addition of prior information aids the estimation process and can make up for a lack of information in the observed dataset. However, careful prior specification may be especially important because the priors compensate for a lack of observed information. Priors placed on the latent covariance matrix in SEMs may be especially important for model estimation when the model is not identified. Other literature (e.g., Liu, Zhang, & Grimm, 2016) has demonstrated how some prior specifications on this component of a growth curve model can lead to biased estimates in identified models. Some prior specifications can lead to model convergence problems and estimated non-positive definite covariance matrices, so the researcher needs to be mindful to assess the impact of their chosen priors.
In this paper, we use weakly informative priors for mean parameters. Weakly informative priors incorporate a small amount of certainty into the analysis. These priors are based on our scale of measurement and used to demonstrate one option for prior specification, but there are many others. Priors may be derived from a data-splitting technique (e.g., Depaoli & van de Schoot, 2017; Gelman, Meng, & Stern, 1996), meta-analysis (e.g., Rietbergen, Klugkist, Janssen, Moons, & Hoijtink, 2011), or expert consultation (e.g., Veen, Stoel, Zondervan-Zwijnenburg, & van de Schoot, 2017). A researcher may also use data from a previous study to specify informative priors. Once all model parameters have priors specified, the researcher can estimate the model.
Posterior distributions are constructed by combining priors with observed data. This combination of observed data and a prior distribution for each parameter leads to a complex, multivariate equation that usually has no simple solution. Statistical software employs iterative algorithms to solve such complex equations regardless of the estimation framework (e.g., frequentist estimation commonly uses maximum likelihood via the expectation-maximization algorithm). Bayesian estimation uses Markov chain Monte Carlo (MCMC), a technique for sampling from a probability distribution, in order to construct posterior distributions.
MCMC sampling uses an iterative process to gather a series of samples from the posterior distribution, which is then used to construct an empirical estimate of the posterior distribution. The “chain” part of MCMC refers to a record of samples from each parameter’s posterior distribution. MCMC sampling in Mplus uses two chains by default, but any number of chains can be specified. To achieve stable and meaningful posterior estimates, the MCMC chains must converge on the posterior distribution. Wildly inconsistent samples from the posterior suggest the chains have not yet converged2 , meaning the posterior distribution estimates are not yet stable. If the posterior estimates are unstable, the researcher cannot draw valid inferences about growth in the population. Therefore, it is crucial for the researcher to assess convergence.
The first several iterations in a chain are usually unstable before the chain “finds” the posterior, and these are referred to as burn-in iterations. After estimating the model and discarding the burn-in iterations (Mplus automatically discards the first half of the MCMC chain), the researcher may check convergence by inspecting plots of parameter estimates in each chain (called trace plots) or by using various convergence diagnostics such as the potential scale reduction factor (PSRF; Brooks & Gelman, 1998). These two diagnostic tools are directly available in Mplus, but additional diagnostics (such as the Geweke statistic, Geweke, 1991) can also be obtained by exporting chains to other software such as the coda package in R (Plummer, Best, Cowles, & Vines, 2006).
Trace plots display post-burn-in iterations on the x-axis and parameter estimates on the y-axis. If a chain has converged, the trace plot should display parameter estimates with a consistent mean (i.e., a stable horizontal band) and a consistent variance (i.e., a stable height of the chain). The researcher must check trace plots for each model parameter. Chains that show inconsistent mean and variance suggest a lack of convergence. Diagnostic statistics are additional tools that are helpful for assessing convergence. The PSRF represents the ratio of within-chain to between-chain variability in post burn-in iterations for a given parameter. Ideally, all MCMC chains will converge to the same probability distribution, and the PSRF will be close to 1.0 for all parameters, but values below 1.1 are considered acceptable. Mplus reports the model’s highest PSRF throughout estimation.
The most common model selection indices used in the Bayesian framework are the deviance information criterion (DIC; Spiegelhalter, Best, Carlin, & van der Linde, 2002, 2014), and Bayesian information criterion (BIC; Schwarz, 1978). Both add a measure of general model fit to a penalty for model complexity. The goal is to balance good fit with parsimony. Among competing models, the model with lowest DIC (or BIC) is preferred. A third index is the posterior predictive p-value (PPP; Gelman et al., 1996; Meng, 1994). Unlike the DIC and BIC, the PPP is a model fit index rather than a model selection index, but it can provide useful information for model selection. These three indices can be used to choose among competing PGCM models.
The PPP is a measure of how well the model explains the observed data by evaluating simulated datasets based on the model. The contrived datasets may fit the model better or worse than the observed data, and the PPP is the proportion of simulated datasets that show more discrepancy from the model than the observed dataset. Mplus conducts these simulations automatically. If simulated data consistently show worse model fit than the observed data, the model does not have good predictive accuracy. On the other hand, if simulated data based on the model always shows better fit than the real data, this also suggests model misfit. A PPP of 0.5 suggests excellent fit, with values close to zero or one suggesting model misspecification. Recent work by Cain and Zhang (2019) suggest using a cutoff of 0.15 or lower to identify model misfit.
After using model comparison indices, it is useful to evaluate the preferred model. Recent developments in Bayesian SEM research have lead to new model fit indices including the Bayesian RMSEA (BRMSEA), the Bayesian comparative fit index (BCFI), and the Bayesian Tucker-Lewis index (BTLI). In addition to point estimates for these indices, Mplus also provides 90% credibility intervals which can provide additional information. In particular, Asparouhov and Muthén (2021a) suggest three interpretations for the BRMSEA credibility interval. If the full interval is below 0.06, BRMSEA suggests the model fits well, but if the full interval is above 0.06, BRMSEA indicates poor fit. If the credibility interval contains the cutoff value 0.06, the fit index is inconclusive (i.e., it cannot determine whether fit is good or bad). The credibility intervals for the other fit indices BCFI and BTLI have a similar interpretation. If the BCFI’s credible interval is above 0.95, it suggests the model is well-fitting. If the interval lies below 0.95, it suggests poor fit. If the credible interval contains 0.95, the fit index is inconclusive. The interpretation of BTLI is the same. Further information on the formulation and use of these fit indices are provided in Asparouhov and Muthén (2021a) and Garnier-Villarreal and Jorgensen (2020).
Bayesian linear PGCMs provide a flexible approach to handling nonlinear trajectories with easily-interpretable parameters3 . To illustrate this approach, we applied Bayesian linear PGCMs to math achievement data using the model selection approach to knot specification. There are many statistical programs that can implement Bayesian PGCMs, including Stan (Stan Development Team, 2019) and OpenBUGS (Spiegelhalter, Thomas, Best, & Lunn, 2007), but we use Mplus for this tutorial because of its popularity and accessibility.
We used math achievement data from the Early Childhood Longitudinal Study, Kindergarten cohort (ECLS-K; Tourangeau, Nord, Lê, Sorongon, & Najarian, 2009) to illustrate Bayesian PGCMs. The ECLS-K dataset is a nationally representative sample from the United States with approximately \(22,000\) children who started kindergarten in the fall of 1998. The full dataset is larger than many datasets in developmental research, so we used a random subsample of \(N = 500\) children to make our demonstration more applicable to common research settings. We also ensured our sample had no missing math measurements to focus our discussion on implemention.
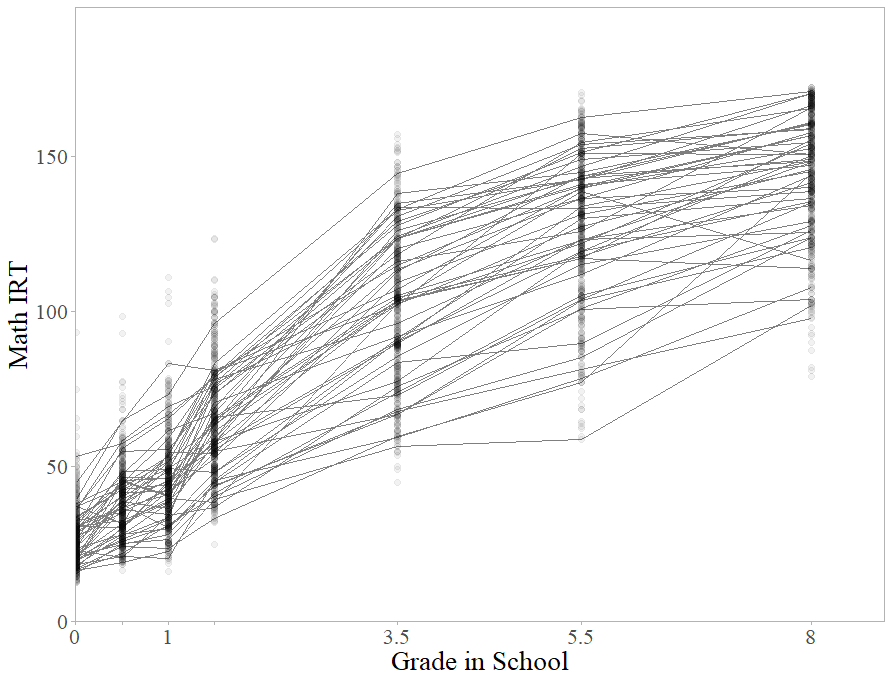
The ECLS-K contains measurements of math achievement from kindergarten through eighth grade. Trained evaluators assessed the children’s math ability in the fall and spring of kindergarten, fall and spring of first grade, the spring of third grade, the spring of fifth grade, and the fall of eighth grade. We coded these times as \(0.0\), \(0.5\), \(1.0\), \(1.5\), \(3.5\), \(5.5\), and \(8.0\). This way, “\(1.0\)” corresponds to fall of first grade, “\(3.5\)” refers to a spring of third-grade measurement, and so on. The Math item response theory (IRT) scores reported in the dataset are scale scores that represent estimates of the number of items children would have answered correctly if they had taken all 174 items at all seven measurement occasions. The IRT scale provided in the ECLS-K ensures that math scores are comparable across test forms. Further details are provided by Pollack, Najarian, Rock, and Atkins-Burnett (2005). Figure 2 shows a scatterplot of the math achievement data across all seven measurement occasions. In the figure, math ability generally increased over time, but some periods of growth were more rapid than others. To estimate a linear PGCM to the nonlinear growth shown in Figure 2, the first step is to determine knot placement. Unlike the simple examples shown in Figure 1, the most appropriate knot specification is not clear. Model selection is one way to address this ambiguity.
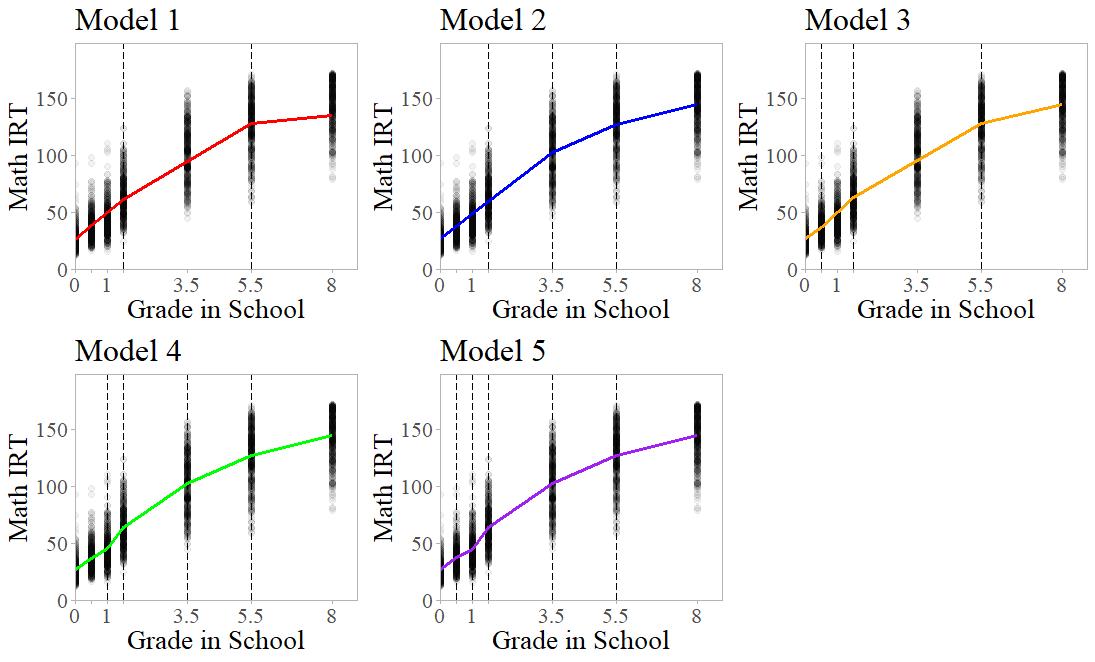
The first step for implementing Bayesian PGCMs is devising a set of model candidates to estimate. The goal is to estimate several models that differ in knot specification and use model selection indices to determine the best model. The only difference between the models should be knot specification. In the Bayesian estimation framework, the researcher may place knots on any measurement occasion except the first and last, and use up to \(J - 2\) knots in total. This means for the ECLS-K data, a researcher may specify a PGCM with anywhere from one to five knots. In this section, we describe five competing models we will use to determine knot specification. The knot placement in these models break up the overall trajectory in up to six phases, visualized in Figure 3. We discuss the rationale behind the knot placement for each model here.
The first knot specification uses a theory-driven approach. According to Piaget’s classic theory of cognitive development (Flavell, 1963), children occupy the preoperational stage of development from ages two to seven. The concrete operational stage occurs from ages seven to eleven, and the formal operational stage begins at twelve years old. These stages represent an increase in childrens’ ability to think abstractly, and a researcher could argue these stages relate to math development. A researcher may apply these phases of development to the ECLS-K data by placing knots at \(k_1=1.5\) and \(k_2=5.5\). For this specification, the first phase of growth corresponds to preoperational development, the second to the concrete operational stage of development, and the third to the formal operational stage. Model 1 implements this knot specification.4
The remaining four models use a data-driven approach to derive knot placement. Model \(2\) divides the trajectory into four almost equally-sized segments by placing knots at \(k_1=1.5, k_2=3.5\), and \(k_3=5.5\). Each phase of growth encompasses 2 years on average, and is the closest to equally-sized segments that is possible with the timing of measurements. The third model places knots at every other measurement occasion: \(k_1=0.5, k_2=1.5\), and \(k_3=5.5\). The fourth model increases complexity to four knots. The scatterplot in Figure 2 may be interpreted to show no meaningful change in growth between the first and second measurement compared to the growth between the second and third. To treat the whole of kindergarten as a single phase of growth while allowing unique phases between all other measurements, Model \(4\) implements four knots \(k_1=1.0\), \(k_2=1.5\), \(k_3=3.5\), and \(k_4=5.5\). Finally, Model \(5\) implements all possible knots \(k_1=0.5\), \(k_2=1.0\), \(k_3=1.5\), \(k_4=3.5\), and \(k_5=5.5\). This fifth model suggests that the rate of change between every single measurement is meaningfully different. In the following sections, we demonstrate how to implement PGCMs in the Bayesian framework and how to use Bayesian model selection indices to choose the most appropriate model.
Each parameter in a model requires a prior. For linear PGCMs, these parameters include coefficient means (for the intercept, first slope, and changes in slope), variances of the coefficients, covariances of the coefficients, and measurement errors. We employed a combination of weakly informative and diffuse priors.
The intercept mean reflects the mean math achievement score when \(t = 0\), or the fall of kindergarten. Visual inspection of the data scatterplot showed no negative values at the first measurement occasion, so the default prior centered on zero did not seem appropriate. Instead, we specified a “weakly informative” prior as Normal(\(\mu \) = 25, \(\sigma ^2\) = 100). The mean of all scores at the first timepoint appears close to 25 in the scatterplot, and setting the variance to 100 reflects our uncertainty about this exact mean value.
After setting the prior for the intercept, we took a more general approach to the priors for the other coefficient means. Setting priors for PGCMs comes with an additional challenge when using model selection indices to determine knot placement: Priors should be kept as consistent as possible across models to ensure that differences in model selection indices are due to knot placement alone. The ECLSK dataset includes math IRT values ranging from approximately 10 to 174. Because of this range of values, the full width of the default priors did not seem useful. A visual inspection of the data scatterplot shows that rate of growth changed over time, but did not appear to exceed 30 IRT points within a single year. In order to keep the priors for the slope means consistent, we assigned a normal prior with N(\(\mu \) = 0, \(\sigma ^2\) = 400) to each one. This reflects our belief that a range of linear slope values from -60 to 60 are possible, with slopes closer to zero more likely. In substantive terms, this means we expected childrens’ math IRT score to change by some value in the -60 to 60 range each year for the first segment of growth, and the rate of change itself would never change by more than 60 points.
Coefficient variances, covariances, and residual variances were also estimated. Because we did not have a clear substantive reason to alter the priors for these parameters, we used Mplus default settings. For the coefficient covariance matrix \(\mathbf {\Sigma _{\delta }}\), Mplus uses an inverse Wishart prior with a \(\mathbf {0}\) scale matrix and –\(p-1\) degrees of freedom, where p is the number of latent growth factors. Residual variances receive an inverse gamma prior defined as IG(\(-1\), \(0\)). Next, we describe how to implement these priors in Mplus.
Estimating Bayesian PGCMs in Mplus requires an input file with five sections: data information (including the DATA and VARIABLE commands), the model itself (under MODEL), estimation details (under ANALYSIS), prior specification (under MODEL PRIORS), and output details (including PLOT and OUTPUT commands). We present the syntax for Model \(5\) here, but readers can implement any of the other candidate models with minor edits to the MODEL and MODEL PRIORS sections. We begin with the MODEL section.
The equation for Model 5 can be written, \begin {equation} \begin {split} y_{ij} &= \delta _{0i} + \delta _{1i}t_{ij} + \delta _{2i}(t_{ij}-0.5)_+ + \delta _{3i}(t_{ij}-1.0)_+ \\ & + \delta _{4i}(t_{ij}-1.5)_+ + \delta _{5i}(t_{ij}-3.5)_+ + \delta _{6i}(t_{ij}-5.5)_+ + e_{ij}, \end {split} \end {equation}
which translates to the following syntax:
MODEL: delta_0 delta_1 | y1@0 y2@0.5 y3@1.0 y4@1.5 y5@3.5 y6@5.5 y7@8.0; delta_0 delta_2 | y1-y2@0 y3@0.5 y4@1.0 y5@3.0 y6@5.0 y7@7.5; delta_0 delta_3 | y1-y3@0 y4@0.5 y5@2.5 y6@4.5 y7@7.0; delta_0 delta_4 | y1-y4@0 y5@2 y6@4 y7@6.5; delta_0 delta_5 | y1-y5@0 y6@2 y7@4.5; delta_0 delta_6 | y1-y6@0 y7@2.5; [delta_0-delta_6] (beta_0-beta_6);
The first line after the MODEL command tells Mplus the timing of all seven measurement occasions, and tells Mplus to use the timing to estimate the intercept and slope of the first phase. The next line contains delta_2 and tells Mplus to estimate the change in slope for the second phase of growth, starting at \(t_{ij} = 0.5\). This line of syntax assigns the values of \((t_{ij} - 0.5)_+\) to each measurement occasion. For the first two measurements, the values are zero. The five time points after the knot are \((t_{ij} - 0.5)_+\) for \(t_{ij} = 1.0\), \(1.5\), \(3.5\), \(5.5\), \(8.0\). For example, the fifth measurement y5 occurs when \(t_{ij}=3.5\). The value of \((3.5 - 0.5)_+ = 3.0\), the value of time assigned to y5. The next four lines of syntax repeat this process for the remaining four phases of growth. In the final line, the square brackets refer to the means of the parameters inside and parentheses contain labels for these means. This line of syntax indicates the mean of the growth coefficients \(\delta _{0i}, \delta _{1i},...,\delta _{6i}\) are labelled \(\beta _{0}, \beta _1,...,\beta _6\).
The next section of code tells Mplus how to estimate the PGCM described above:
ANALYSIS: ESTIMATOR=BAYES; FBITERATIONS = 100000; BSEED = 1979;
The first line under the ANALYSIS heading tells Mplus that we want to use Bayesian estimation. The next command, FBITERATIONS = 100000, requests \(100\),\(000\) MCMC iterations. This number was selected based on the number of iterations required for Model \(5\) to converge according to PSRF. Next, the BSEED = 1979 command provides Mplus a “seed” number to begin implementing the MCMC algorithm. We provide one here so the reader may replicate our results, but Mplus can generate its own if one is not provided. If the model reaches convergence, the seed number does not influence model results.
Next, priors are specified in the MODEL PRIORS section:
MODEL PRIORS: beta_0 ~ N(25, 100); beta_1-beta_6 ~ N(0, 400);
The first line under the MODEL PRIORS heading tells Mplus that the mean of the intercept is normally distributed around 25 with a variance of 100, or \(\beta _0 \sim N(25, 100)\). The next line assigns a prior to the means of all six slope parameters, \(\beta _1\), \(\beta _2,..., \beta _6 \sim N(0, 400)\). We do not explicitly assign variance priors here, so Mplus will use its diffuse defaults. Once each candidate model’s input file has been written in Mplus, we can estimate the models and use the results to conduct model selection.
The five candidate models provide slightly different descriptions of change in math achievement over time, as illustrated in Figure 3. The next step of the process is to examine Bayesian model selection indices summarized in Table 1 to choose the best model. For the PPP, values close to 0.500 suggest excellent fit, and values close to zero or one suggest poor fit. For the DIC and BIC, the lowest value suggests the best balance of model fit with model complexity. In this case, the PPP and DIC suggest that Model 5 is the best model. However, the BIC suggests the best model is Model 4. For the purposes of this illustration, we consider Model 5 the optimal model.
| Fit indices for model selection | |||||
| Fit Index | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 |
| PPP | 0.000 | 0.000 | 0.000 | 0.001 | 0.468 |
| DIC | 26533.70 | 26245.22 | 26486.75 | 26023.36 | 25992.85 |
| BIC | 26626.34 | 26371.32 | 26615.68 | 26229.44 | 26458.46 |
| Approximate fit indices for evaluating Model 5
| |||||
| Fit Index | Point Estimate | 90% Credible Interval | |||
| BRMSEA | 0.031 | [0.000, 0.158] | |||
| BCFI | 1.000 | [0.995, 1.000] | |||
| BTLI | 0.997 | [0.925, 1.000] | |||
We can evaluate the quality of Model 5 using the BRMSEA, BCFI, and BTLI. The point estimates and 90% credible intervals for these fit indices are reported in Table 1. We focus on the credibility intervals to keep our interpretation consistent with Asparouhov and Muthén (2021a). For the BRMSEA, values below 0.06 indicate good model fit. The BRMSEA’s credible interval ranged from zero to 0.158. Because the credible interval contained 0.06, this fit index is inconclusive. Next, we consider the BCFI and BTLI, where values between 0.95 and 1.00 suggest excellent fit. For the BCFI, the credible interval ranged from 0.995 to 1.000, and the BTLI credible interval ranged from 0.925 to 1.000. The BCFI results suggest good model fit because the credible interval is entirely above 0.95. However, the BTLI credible interval contains the cutoff value and we consider this fit index inconclusive. In summary, one fit index suggested good fit but the other two were inconclusive.
Next, we describe and interpret the parameter estimates for Model \(5\), which are summarized in Table 2. Recall that \(\beta _0\) and \(\beta _1\) refer to the mean intercept and linear slope for the first phase of growth, and each following coefficient from \(\beta _2\) to \(\beta _6\) refer to an average change in slope. In other words, the mean rate of change in the second slope is not the estimate of \(\beta _2\) alone, but the sum of \(\beta _1 + \beta _2\). These changes accumulate across the phases of growth. For ease of interpretation, Table 2 contains a “Total Slope” column that reflects the rate of change in all six phases. For example, the total slope in the first phase of growth (from fall of kindergarten to spring of kindergarten) is 21.28. This value means that children’s math achievement would increase by an average of 21.28 points in one year if growth remained constant. The rate of growth in the second phase of development (spring of kindergarten to fall of first grade) decreases by -6.89, resulting in a rate of 14.39. In contrast, the third phase of development (from fall to spring of first grade) showed an increase in growth of 22.95, leading to a total slope of 37.34. The fourth phase of growth addresses two years of growth from spring of first grade to the spring of third grade. The average rate of change per year in this phase decreased from the previous phase by -18.02, meaning childrens’ math achievement increased by 19.32 per year on average. In the fifth phase, growth slowed again by -6.90, creating a 12.42 increase in math achievement per year from spring of third grade to the spring of fifth grade. In the final phase from spring of fifth grade to fall of eighth grade, growth slowed by -5.61 to a rate of change of 6.81. Overall, growth was most rapid in the third phase, which was also when the most dramatic change in the rate of development occurred. Table 2 also reports measurement error variance at all seven timepoints, which ranged from 10.60 at the first measurement to 39.84 at the fifth measurement.
We present the covariance matrix of the growth coefficients \(\mathbf {\Sigma _{\delta }}\) in the lower portion of Table 2. The individual elements in this matrix are not typically of interest, but we can note that each coefficient covaries with the others. There are particularly strong negative covariances between \(\delta _{1i}\) and \(\delta _{2i}\), \(\delta _{2i}\) and \(\delta _{3i}\), and \(\delta _{3i}\) and \(\delta _{4i}\). In other words, the rate of change in one phase of growth tends to increase when the next phase decreases, and this relationship is particularly strong across the first, second, third, and fourth phases. We can also note that the change in slope for the second, third, and fourth phases show the highest variance of all latent growth coefficients.
| Growth Factor Estimates, Standard Errors, and Phase-Specific Slopes
| |||||||
| Coefficient | Estimate(SE) | Total Slope | |||||
| \(\beta _0\) | 27.25(0.43) | ||||||
| \(\beta _1\) | 21.28(0.65) | 21.28 | |||||
| \(\beta _2\) | -6.89(1.16) | 14.39 | |||||
| \(\beta _3\) | 22.95(1.37) | 37.34 | |||||
| \(\beta _4\) | -18.02(1.09) | 19.32 | |||||
| \(\beta _5\) | -6.90(0.51) | 12.42 | |||||
| \(\beta _6\) | -5.61(0.41) | 6.81 | |||||
| Error Variances
| |||||||
| \(\sigma ^2_{e1}\) | 10.60(7.22) | ||||||
| \(\sigma ^2_{e2}\) | 11.78(9.08) | ||||||
| \(\sigma ^2_{e3}\) | 20.79(11.29) | ||||||
| \(\sigma ^2_{e4}\) | 32.56(21.58) | ||||||
| \(\sigma ^2_{e5}\) | 39.84(25.54) | ||||||
| \(\sigma ^2_{e6}\) | 30.56(20.15) | ||||||
| \(\sigma ^2_{e7}\) | 39.30(29.67) | ||||||
| Covariance Matrix \(\Sigma _{\delta }\)
| |||||||
| Coefficient | \(\delta _0\) | \(\delta _1\) | \(\delta _2\) | \(\delta _3\) | \(\delta _4\) | \(\delta _5\) | \(\delta _6\) |
| \(\delta _0\) | 82.76 | ||||||
| \(\delta _1\) | 16.00 | 116.89 | |||||
| \(\delta _2\) | 18.311 | -159.98 | 354.63 | ||||
| \(\delta _3\) | -15.54 | 78.13 | -239.28 | 438.00 | |||
| \(\delta _4\) | -3.56 | -21.58 | 38.03 | -274.32 | 299.31 | ||
| \(\delta _5\) | -22.39 | -13.93 | 8.03 | 0.68 | -40.00 | 68.88 | |
| \(\delta _6\) | -4.55 | -9.14 | 5.05 | -7.25 | 9.07 | -19.54 | 40.18 |
In this application, we devised a set of candidate models and used model selection indices to determine the most adequate model. The final model was Model 5, which treats the time between each measurement occasion as a distinct phase of growth with its own unique rate of change. The BCFI suggested good model fit, but other approximate fit indices were inconclusive. We interpreted these results as not suggesting excellent fit, but not suggesting substantial misfit either. According to this model, the most rapid growth occurred in the third phase, from fall to spring of first grade. After this phase, the rate of growth decreased in each subsequent phase.
Our goal for this paper was to demonstrate how linear PGCMs are a flexible extension of linear GCMs, with models addressing three or more phases of growth possible in the Bayesian estimation framework. This added flexibility can dramatically increase the number of possible models, and we outlined the process of specifying candidate models and using model selection indices to choose the final model. To provide a simple and accessible tutorial to implement Bayesian linear PGCMs, several extensions and technical features were not addressed in detail. We discuss extensions of the presented model and some technical cautions here.
In this tutorial, we focused on Bayesian linear PGCMs due to their simple coefficient interpretations in order to provide an introduction to the field of piecewise growth models. As noted previously, there are several newer extensions of the presented model, which we encourage readers to explore. These extensions include piecewise models that directly estimate knot placements (Kohli et al., 2015; Lock et al., 2018), employ covariates (Lamm, 2022), or capture bivariate piecewise trajectories (Peralta et al., 2022). Additionally, PGCMs with higher-order polynomials (e.g., cubic) or inherently nonlinear functions (e.g., exponential) are also possible. Harring, Strazzeri, and Blozis (2021) provide a discussion of these extensions in the context of PGCMs with random knots. Additionally, Rioux, Stickley, and Little (2021) demonstrate PGCMs with discontinuities (i.e., gaps in the growth trajectory) to address cancelled data collection waves. Piecewise models with inconsistent measurement timing can be easily addressed in the multilevel modeling framework, where they are commonly called splines. Harezlak, Ruppert, and Wand (2018) provide a thorough introduction, including Bayesian extensions.
Implementing linear PGCMs in the Bayesian estimation framework frees the researcher from model identification requirements inherent in frequentist estimation because prior distributions can compensate for additional measurement occasions. However, implementing non-identified models in the Bayesian framework must be done cautiously. The prior placed on the latent covariance matrix can be especially influential on model results, as shown by Liu et al. (2016) and Depaoli, Liu, and Marvin (2021). The specific implementation of the inverse Wishart prior (the Mplus default) can also impact results in unexpected ways. A key method of assessing how sensitive results are to prior specification is to conduct a prior sensitivity analysis. In a prior sensitivity analysis, the researcher estimates the chosen model under a set of alternative prior conditions, and discusses how robust the model results are. We recommend van Erp, Mulder, and Oberski (2018), van de Schoot, Veen, Smeets, Winter, and Depaoli (2020), and Depaoli, Winter, and Visser (2020) for thorough demonstrations. When implemented conscientiously, we believe Bayesian linear PGCMs can be a useful class of models because they frame development as phases of growth with simple parameters. This is in contrast to other GCM extensions with parameters that may be challenging to interpret (e.g., a cubic coefficient).
Developmental researchers study within-person change over time in many settings. A linear GCM easily captures growth that follows a straight line, but may not capture substantively important nonlinear changes. In this paper we presented a tutorial to estimate Bayesian PGCMs, which can handle complex nonlinearity with simple parameter interpretations. The goal of this tutorial was specifically aimed to act as a precursor to more advanced methodological work (e.g., Kohli et al., 2015), which we recommend the interested reader to explore as a subsequent resource to this work.
Applying this model to math achievement data allowed us to examine when development accelerated or slowed, and highlighted phases of growth with more variability than others. Bayesian PGCMs provide researchers with a useful model that can capture nonlinear growth using parameters that are straightforward to interpret. While research is needed to better understand the impact of different covariance priors, the Bayesian linear PGCM can provide interesting results when implemented thoughtfully.
Akaike, H. (1992). Information theory and an extension of the maximum likelihood principle. In Breakthroughs in statistics (pp. 610–624). Springer.
Asparouhov, T., & Muthén, B. (2021a). Advances in Bayesian model fit evaluation for structural equation models. Structural Equation Modeling: A Multidisciplinary Journal, 28, 1–14. doi: https://doi.org/10.1080/10705511.2020.1764360
Asparouhov, T., & Muthén, B. (2021b). Bayesian analysis of latent variable models using mplus (version 5). mPlus. Retrieved from https://www.statmodel.com/download/BayesAdvantages18.pdf
Bentler, P. M. (1990). Comparative fit indexes in structural models. Psychological bulletin, 107(2), 238.
Bollen, K. A., & Curran, P. J. (2006). Latent curve models: A structural equation perspective (Vol. 467). John Wiley & Sons.
Brooks, S. P., & Gelman, A. (1998). General methods for monitoring convergence of iterative simulations. Journal of Computational and Graphical Statistics, 7(4), 434–455.
Browne, M. W., & Cudeck, R. (1992). Alternative ways of assessing model fit. Sociological methods & research, 21(2), 230–258.
Cain, M. K., & Zhang, Z. (2019). Fit for a Bayesian: An evaluation of ppp and dic for structural equation modeling. Structural Equation Modeling: A Multidisciplinary Journal, 26, 39–50. doi: https://doi.org/10.1080/10705511.2018.1490648
Depaoli, S. (2013). Mixture class recovery in GMM under varying degrees of class separation: Frequentist versus Bayesian estimation. Psychological Methods, 18(2), 186–219. doi: https://doi.org/10.1037/a0031609
Depaoli, S. (2021). Bayesian structural equation modeling. The Guilford Press.
Depaoli, S., Liu, H., & Marvin, L. (2021). Parameter specification in Bayesian CFA: An exploration of multivariate and separation strategy priors. Structural Equation Modeling: A Multidisciplinary Journal, 28(5), 1–17. doi: https://doi.org/10.1080/10705511.2021.1894154
Depaoli, S., & van de Schoot, R. (2017). Improving transparency and replication in Bayesian statistics: The WAMBS-checklist. Psychological methods, 22(2), 240. doi: https://doi.org/10.1037/met0000065
Depaoli, S., Winter, S. D., & Visser, M. (2020). The importance of prior sensitivity analysis in Bayesian statistics: Demonstrations using an interactive Shiny app. Frontiers in Psychology, 11. doi: https://doi.org/10.3389/fpsyg.2020.608045
Finkel, D., Reynolds, C. A., McArdle, J. J., & Gatz, N. L., M. Pedersen. (2003). Latent growth curve analyses of accelerating decline in cognitive abilities in late adulthood. Developmental Psychology, 39(3), 535–550. doi: https://doi.org/10.1037/0012-1649.39.3.535
Flavell, J. H. (1963). The developmental psychology of Jean Piaget. D van Nostrand.
Flora, D. B. (2008). Specifying piecewise latent trajectory models for longitudinal data. Structural Equation Modeling: A Multidisciplinary Journal, 15(3), 513–533. doi: https://doi.org/10.1080/10705510802154349
Garnier-Villarreal, M., & Jorgensen, T. D. (2020). Adapting fit indices for Bayesian structural equation modeling: Comparison to maximum likelihoods. Psychological Methods, 25(1), 46–70. doi: https://doi.org/10.1037/met0000224
Gaudreau, P., Louvet, B., & Kljajic, K. (2018). The performance trajectory of physical education students differs across subtypes of perfectionism: A piecewise growth curve model of the 2 \(\times \) 2 model of perfectionism. Sport, Exercise, and Performance Psychology, 8(2), 223–237. doi: https://doi.org/10.1037/spy0000138
Gelman, A., Meng, X.-L., & Stern, H. (1996). Posterior predictive assessment of model fitness via realized discrepancies. Statistica Sinica, 733–760.
Geweke, J. F. (1991). Evaluating the accuracy of sampling-based approaches to the calculation of posterior moments (Tech. Rep.). Federal Reserve Bank of Minneapolis.
Grimm, K. J., & Ram, N. (2009). Nonlinear growth models in Mplus and SAS. Structural Equation Modeling, 16(4), 676–701. doi: https://doi.org/10.1080/10705510903206055
Harezlak, J., Ruppert, D., & Wand, M. P. (2018). Semiparametric regression with r. Springer.
Harring, J. R., Strazzeri, M. M., & Blozis, S. A. (2021). Piecewise latent growth models: beyond modeling linear-linear processes. Behavior Research Methods, 53(2), 593–608.
Kohli, N., Hughes, J., Wang, C., Zopluoglu, C., & Davison, M. L. (2015). Fitting a linear–linear piecewise growth mixture model with unknown knots: A comparison of two common approaches to inference. Psychological methods, 20(2), 259.
Kruschke, J. (2014). Doing Bayesian data analysis: A tutorial with R, JAGS, and Stan. Academic Press.
Lamm, R. Z. (2022). Incorporation of covariates in bayesian piecewise growth mixture models (Unpublished doctoral dissertation). University of Minnesota.
Liu, H., Zhang, Z., & Grimm, K. J. (2016). Comparison of inverse Wishart and separation-strategy priors for Bayesian estimation of covariance parameter matrix in growth curve analysis. Structural Equation Modeling: A Multidisciplinary Journal, 23(3), 354–367. doi: https://doi.org/10.1080/10705511.2015.1057285
Lock, E. F., Kohli, N., & Bose, M. (2018). Detecting multiple random changepoints in bayesian piecewise growth mixture models. Psychometrika, 83, 733–750.
Marks, A., & Coll, C. G. (2007). Psychological and demographic correlates of early academic skill development among American Indian and Alaska Native youth: A growth modeling study. Developmental Psychology, 43(3), 663–674. doi: https://doi.org/0.1037/0012-1649.43.3.663
Meng, X.-L. (1994). Posterior predictive \( p \)-values. The annals of statistics, 22(3), 1142–1160.
Meredith, W., & Tisak, J. (1990). Latent curve analysis. Psychometrika, 55(1), 107–122.
Nylund, K. L., Asparouhov, T., & Muthén, B. O. (2007). Deciding on the number of classes in latent class analysis and growth mixture modeling: A Monte Carlo simulation study. Structural equation modeling: A multidisciplinary Journal, 14(4), 535–569.
Peralta, Y., Kohli, N., Lock, E. F., & Davison, M. L. (2022). Bayesian modeling of associations in bivariate piecewise linear mixed-effects models. Psychological methods.
Plummer, M., Best, N., Cowles, K., & Vines, K. (2006). Coda: Convergence diagnosis and output analysis for MCMC. R News, 6(1), 7–11. Retrieved from https://journal.r-project.org/archive/
Pollack, J. M., Najarian, M., Rock, D. A., & Atkins-Burnett, S. (2005). Early childhood longitudinal study, kindergarten class of 1998-99 (ECLS-K): Psychometric report for the fifth grade. NCES 2006-036. National Center for Education Statistics.
Rietbergen, C., Klugkist, I., Janssen, K. J., Moons, K. G., & Hoijtink, H. J. (2011). Incorporation of historical data in the analysis of randomized therapeutic trials. Contemporary Clinical Trials, 32(6), 848–855. doi: https://doi.org/10.1016/j.cct.2011.06.002
Rioux, C., Stickley, Z. L., & Little, T. D. (2021). Solutions for latent growth modeling following COVID-19-related discontinuities in change and disruptions in longitudinal data collection. International Journal of Behavioral Development, 45(5), 463–473. doi: https://doi.org/10.1177/01650254211031631
Schillin, O. K., Deeg, D. J. H., & Huisman, M. (2018). Affective well-being in the last years of life: The role of health decline. Psychology and Aging, 33(5), 739–753. doi: https://doi.org/10.1037/pag0000279
Schwarz, G. (1978). Estimating the dimension of a model. The Annals of Statistics, 461–464.
Seider, S., Clark, S., Graves, D., Kelly, L. L., Soutter, M., El-Aamin, A., & Jennett, P. (2019). Black and latinx adolescents’ developing beliefs about poverty and associations with their awareness of racism. Developmental Psychology, 55(3), 509–524. doi: https://doi.org/10.1037/dev0000585
Shono, Y., Edwards, M. C., Ames, S. L., & Stacy, A. W. (2018). Trajectories of cannabis-related associative memory among vulnerable adolescents: Psychometric and longitudinal evaluations. Developmental Psychology, 54(6), 1148–1158. doi: https://doi.org/10.1037/dev0000510
Spiegelhalter, D., Best, N. G., Carlin, B. P., & van der Linde, A. (2002). Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society, 64(4), 583–639. doi: https://doi.org/10.1111/1467-9868.00353
Spiegelhalter, D., Best, N. G., Carlin, B. P., & van der Linde, A. (2014, April). The deviance information criterion: 12 years on. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 76(3), 485–493. doi: https://doi.org/10.1111/rssb.12062
Spiegelhalter, D., Thomas, A., Best, N., & Lunn, D. (2007). OpenBUGS user manual. Version, 3(2), 2007.
Stan Development Team. (2019). Stan modeling language users guide and reference manual, version 2.28.0. Retrieved from http://mc-stan.org/
Steiger, J. H., & Lind, J. C. (1980). Statistically based tests for the number of common factors. In The annual meeting of the Psychometric Society. Iowa City, IA.
Tourangeau, K., Nord, C., Lê, T., Sorongon, A. G., & Najarian, M. (2009). Early childhood longitudinal study, kindergarten class of 1998-99 (ECLS-K): Combined user’s manual for the ECLS-K eighth-grade and K-8 full sample data files and electronic codebooks. NCES 2009-004. National Center for Education Statistics.
Tucker, L. R., & Lewis, C. (1973). A reliability coefficient for maximum likelihood factor analysis. Psychometrika, 38(1), 1–10.
van de Schoot, R., Veen, D., Smeets, L., Winter, S. D., & Depaoli, S. (2020). A tutorial on using the wambs checklist to avoid the misuse of bayesian statistics. Small Sample Size Solutions: A Guide for Applied Researchers and Practitioners; van de Schoot, R., Miocevic, M., Eds, 30–49.
van Erp, S., Mulder, J., & Oberski, D. L. (2018). Prior sensitivity analysis in default Bayesian structural equation modeling. Psychological Methods, 23(2), 363–388. doi: https://doi.org/10.3758/s13428-011-0088-6
Vargas Lascano, D. I., Galambos, N. L., Krahn, H. J., & Lachman, M. E. (2015). Growth in perceived control across 25 years from the late teens to midlife: The role of personal and parents’ education. Developmental Psychology, 51(1), 124–135. doi: https://doi.org/10.1037/a0038433
Veen, D., Stoel, D., Zondervan-Zwijnenburg, M., & van de Schoot, R. (2017). Proposal for a five-step method to elicit expert judgment. Frontiers in psychology, 8, 2110. doi: https://doi.org/10.3389/fpsyg.2017.02110
Wang, L., & McArdle, J. J. (2008). A simulation study comparison of Bayesian estimation with conventional methods for estimating unknown change points. Structural Equation Modeling: A Multidisciplinary Journal, 15(1), 52–74. doi: https://doi.org/10.1080/10705510701758265
Zimmer-Gembeck, M., Gardner, A. A., Hawes, T., Maters, M. R., Waters, A. M., & Farrell, L. J. (2021). Rejection sensitivity and the development of social anxiety symptoms during adolescence: A five-year longitudinal study. International Journal of Behavioral Development, 45(3), 204–215. doi: https://doi.org/10.1177/0165025421995921
To demonstrate the utility of treating the knot specification problem as a model selection problem, we performed a simulation study. The purpose of this study was twofold. First, we aimed to evaluate the performance of Bayesian model fit indices in selecting the correct knot specification. Second, we assessed the accuracy of the model parameter estimates.
We considered five population models based on the five candidate models used in analyzing the ECLS-K (see Figure 3). There are seven measurement occasions, coded like the ECLS-K such that \(t = 0.0, 0.5, 1.0, 1.5, 3.5, 5.5, 8.0\). For Population Model 1, growth was split into three phases, with knots at \(t = 1.5, 5.5\). Both Population Model 2 and Population Model 3 had four phases in the growth trajectory but different knot placements. Population Model 2 used knots at \(t = 1.5, 3.5, 5.5\) and Population Model 3 used knots at \(t = 0.5, 1.5, 5.5\). Population Model 4 implemented five phases of growth with knots at \(t = 1.0, 1.5, 3.5, 5.5\). Population Model 5 split the trajectory into six unique phases of growth, with as many knots as possible at \(t = 0.5, 1.0, 1.5, 3.5, 5.5\).
The distribution of the latent growth factors for the five population models were based on the ECLS-K estimates. The distribution of growth factors for Population Model 1 through 5 are described in the following Equations (15) through (19):
\begin {align} \begin {bmatrix}\delta _0\\ \delta _1\\ \delta _2\\ \delta _3 \end {bmatrix} \sim MVN\left ( \begin {bmatrix}26.71\\ 23.10\\ -6.50\\ -9.95 \end {bmatrix}, \begin {bmatrix} 75.00 &&&\\ 29.96 & 30.65 &&\\ -27.03 & -20.70 & 20.95&\\ -14.36 & -19.69 & 2.57 & 39.17\\ \end {bmatrix} \right ), \end {align}
\begin {align} \begin {bmatrix}\delta _0\\ \delta _1\\ \delta _2\\ \delta _3\\ \delta _4 \end {bmatrix} \sim MVN\left ( \begin {bmatrix}26.93\\ 21.83\\ -0.44\\ -8.96\\ -5.61 \end {bmatrix}, \begin {bmatrix} 76.71 &&&&\\ 28.20 & 26.45 &&&\\ -14.68 & -5.82 & 17.83 &&\\ -20.18 & -21.62 & -16.97 & 63.61 &\\ -4.46 & -7.83 & 5.58 & -19.30 & 38.86 \\ \end {bmatrix} \right ), \end {align}
\begin {align} \begin {bmatrix}\delta _0\\ \delta _1\\ \delta _2\\ \delta _3\\ \delta _4 \end {bmatrix} \sim MVN\left ( \begin {bmatrix}27.26\\ 19.34\\ 6.68\\ -9.83\\ -9.55 \end {bmatrix}, \begin {bmatrix} 85.00 &&&&\\ 10.38 & 62.49 &&&\\ 20.30 & -36.14 & 64.72 &&\\ -27.56 & -16.60 & -30.99 & 52.06 &\\ -15.15 & -15.70 & -2.80 & 0.80 & 38.89 \\ \end {bmatrix} \right ), \end {align}
\begin {align} \begin {bmatrix}\delta _0\\ \delta _1\\ \delta _2\\ \delta _3\\ \delta _4 \\ \delta _5 \end {bmatrix} \sim MVN\left ( \begin {bmatrix}27.57\\ 18.22\\ 17.75\\ -16.63\\ -6.90\\ -5.60 \end {bmatrix}, \begin {bmatrix} 76.61&&&&&\\ 29.66 & 29.19 &&&&\\ -8.32 & 9.03 & 171.87 &&&\\ -5.40 & -27.60 & -197.26 & 270.61 &&\\ -22.58 & -10.42 & 9.72 & -41.46 & 64.09 &\\ -4.74 & -6.90 & -3.12 & 6.87 & -16.44 & 38.54 \\ \end {bmatrix} \right ), \end {align}
\begin {align} \begin {bmatrix}\delta _0\\ \delta _1\\ \delta _2\\ \delta _3\\ \delta _4\\ \delta _5\\ \delta _6 \end {bmatrix} \sim MVN\left ( \begin {bmatrix}27.25\\ 21.29\\ -6.89\\ 22.95\\ -18.02\\ -6.50\\ -5.61 \end {bmatrix}, \begin {bmatrix} 82.76 &&&&&&\\ 16.00 & 116.89 &&&&&\\ 18.31 & -159.98 & 116.89 &&&&\\ -15.54 & 78.13 & -239.28 & 438.00 &&&\\ -3.56 & -21.58 & 38.03 & -274.32 & 299.31 &&\\ -22.39 & -13.93 & 8.03 & 0.68 & -40.00 & 68.88 &\\ -4.55 & -9.14 & 5.05 & -7.25 & 9.07 & -19.54 & 40.18 \\ \end {bmatrix} \right ). \end {align}
Measurement error variances were set to 1.0. For each population model, we simulated 500 datasets with sample size \(N = 500\). For each generated dataset, we fit all five candidate models, including the true model and the models with misspecified knot placement. We estimated each model using Bayesian estimation methods with the same setup (i.e., prior specification, number of iterations) as that in analyzing the ECLS-K data. For each replication and model fitted, we recorded the model parameter estimates and the Bayesian model fit indices PPP, DIC, and BIC.
Table 3 shows the selection rates for the PPP, DIC, and BIC within all five population models. To compute the selection rate of the PPP, we found the proportion of replications where a given model had a PPP value closer to 0.5 than all competing models. The selection rate of the DIC was the proportion of replications where a given model had a lower DIC than all competing models. The BIC selection rate was computed the same way5 .
When the data were generated from Model 1, the selection rate of PPP for the correct model (i.e., Model 1) was around 11%. Similarly, when the data were generated from Model 2, the selection rate of PPP for the correct model was 16%. When data were generated from Model 3, PPP selected Model 3 28% of the time, and when data were generated from Model 4, PPP selected Model 4 28% of the time. For Population Model 5, the PPP selected the correct model (i.e., Model 5) 100% of the time. Based on the simulation results, the PPP tends to select more complex models. However, the DIC and BIC were more effective at selecting the correct model. When the data were generated from Model 1, the DIC selected the correct model (i.e., Model 1) 86% of the time. When the data were generated from Model 2, DIC selected Model 2 92% of the time, and when data were generated from Model 3, DIC selected Model 3 98% of the time. For data generated from Model 4, the DIC selected Model 4 with a 93% selection rate. Lastly, when data were generated from Model 5, the DIC selected Model 5 100% of the time. The BIC showed generally high selection rates for the correct model. When the data were generated from Model 1, the BIC selected Model 1(i.e., the correct model) 100% of the time. The BIC selected the correct model 100% of the time when data was generated from Model 2, Model 3, and Model 4. However, when the data were generated from Model 5, the BIC selected Model 5 only 1.2% of the time.
Table 4 reports the mean relative bias for coefficient estimates for the five estimated models across all five population models. Relative bias was computed as the difference between a parameter estimate and its true value, divided by the true value. The highest relative bias for a correct model was 1.04% for Model 2’s \(\beta _2\). Otherwise, relative bias for the true population model never exceeded 1%.
Overall, these results suggest that the DIC and BIC can effectively select an appropriate knot specification among competing models in most conditions. In general, the BIC selected the correct model more often than the DIC. A major exception to this occurred for data generated from Population Model 5. When data were generated from Model 5, the BIC selected Model 4 (an incorrect and less-complex model) 99% of the time but the DIC selected Model 5 (the correct model) 100% of the time. The PPP does not seem to reliably select the correct model when models with more phases are available. When the correct model is selected, growth factor means are estimated with very little bias. While these results provide evidence that the Bayesian PGCM demonstrated in this tutorial is a useful tool for handling complex nonlinear trajectories, a more thorough simulation study is needed to examine whether this pattern of results holds across different research conditions.
| Population | Estimated | PPP | DIC | BIC |
Population
Model
1 | Model 1 | 0.11 | 0.86 | 1.00 |
| Model 2 | 0.12 | 0.06 | 0.00 | |
| Model 3 | 0.13 | 0.07 | 0.00 | |
| Model 4 | 0.27 | 0.01 | 0.00 | |
| Model 5 | 0.36 | 0.00 | 0.00 | |
Population
Model
2 | Model 1 | 0.00 | 0.00 | 0.00 |
| Model 2 | 0.16 | 0.92 | 1.00 | |
| Model 3 | 0.00 | 0.00 | 0.00 | |
| Model 4 | 0.24 | 0.06 | 0.00 | |
| Model 5 | 0.61 | 0.02 | 0.00 | |
Population
Model
3 | Model 1 | 0.00 | 0.00 | 0.00 |
| Model 2 | 0.00 | 0.00 | 0.00 | |
| Model 3 | 0.23 | 0.98 | 1.00 | |
| Model 4 | 0.00 | 0.00 | 0.00 | |
| Model 5 | 0.77 | 0.02 | 0.00 | |
Population
Model
4 | Model 1 | 0.00 | 0.00 | 0.00 |
| Model 2 | 0.00 | 0.00 | 0.00 | |
| Model 3 | 0.00 | 0.00 | 0.00 | |
| Model 4 | 0.28 | 0.93 | 1.00 | |
| Model 5 | 0.72 | 0.07 | 0.00 | |
Population
Model
5 | Model 1 | 0.00 | 0.00 | 0.00 |
| Model 2 | 0.00 | 0.00 | 0.00 | |
| Model 3 | 0.00 | 0.00 | 0.00 | |
| Model 4 | 0.00 | 0.00 | 0.99 | |
| Model 5 | 1.00 | 1.00 | 0.01 | |
| Population | Estimated | \(\beta _0\) | \(\beta _1\) | \(\beta _2\) | \(\beta _3\) | \(\beta _4\) | \(\beta _5\) | \(\beta _6\) |
Population
Model
1 | Model 1 | -0.19 | -0.07 | -0.21 | -0.16 | |||
| Model 2 | -0.19 | -0.06 | -0.19 | -100.03 | ||||
| Model 3 | -0.18 | -0.07 | -100.01 | -34.80 | ||||
| Model 4 | -0.20 | -0.06 | -99.96 | -34.83 | ||||
| Model 5 | -0.20 | -0.06 | -99.97 | -99.96 | ||||
Population
Model
2 | Model 1 | -0.07 | -0.01 | 982.00 | 17.17 | |||
| Model 2 | -0.04 | -0.08 | -1.04 | 0.27 | 0.08 | |||
| Model 3 | -0.04 | -0.13 | -108.01 | -46.79 | 67.24 | |||
| Model 4 | -0.06 | -0.09 | -100.74 | -95.11 | 59.25 | |||
| Model 5 | -0.06 | -0.09 | -99.55 | -100.04 | -92.18 | |||
Population
Model
3 | Model 1 | -10.54 | 32.33 | -240.20 | -2.42 | |||
| Model 2 | -10.05 | 31.58 | -237.04 | -98.97 | -0.10 | |||
| Model 3 | -0.04 | -0.13 | -0.00 | -0.22 | -0.12 | |||
| Model 4 | -5.04 | 24.10 | -69.86 | -0.01 | -100.02 | |||
| Model 5 | -0.06 | -0.12 | -0.07 | -100.00 | 2.68 | |||
Population
Model
4 | Model 1 | -0.43 | 1.80 | -102.80 | -32.32 | |||
| Model 2 | -0.18 | 0.91 | -70.09 | -32.40 | -18.46 | |||
| Model 3 | 0.02 | -0.04 | -89.94 | -86.17 | 58.06 | |||
| Model 4 | 0.00 | 0.02 | -0.23 | -0.31 | 0.07 | 0.27 | ||
| Model 5 | 0.00 | 0.05 | -100.06 | -206.53 | 140.32 | 23.33 | ||
Population
Model
5 | Model 1 | -1.39 | 7.79 | -6.60 | -142.37 | |||
| Model 2 | -0.74 | 0.87 | -102.51 | -139.94 | -69.01 | |||
| Model 3 | 0.03 | -9.35 | -202.68 | -145.14 | -48.82 | |||
| Model 4 | 0.77 | -14.95 | -365.47 | -174.41 | -61.66 | -19.19 | ||
| Model 5 | 0.02 | -0.10 | -0.93 | -0.38 | -0.15 | 0.09 | -0.60 | |