Item response modeling is common throughout psychology and education in assessments of intelligence, psychopathology, and ability. The current paper provides a tutorial on estimating the two-parameter logistic and graded response models in a Bayesian framework as well as provide an introduction on evaluating convergence and model fit in this framework. Example data are drawn from depression items in the 2017 Wave of the National Longitudinal Survey of Youth and example code is provided for JAGS and implemented through R using the runjags package. The aim of this paper is to provide readers with the necessary information to conduct Bayesian IRT in JAGS.
Keywords: Logistic Response Model · Item Response Theory · Bayesian Method · JAGS Tutorial
Item response theory (IRT) is a psychometric framework for modeling relationships between observed responses, often in the form of test or survey data, and latent abilities or traits (Birnbaum, 1968; Embretson & Reise, 2000). IRT models consist of two sets of parameters namely ability parameters \(\theta _i\), \(i=1, \space 2, \space ... \space N\), and item parameters \(\pmb {\omega _j}\), \(j = 1, \space 2, \space ... \space J\) where \(i\) indexes the number of respondents and \(j\) indexes the test items. Thus, the sample size is \(N\) and test length is \(J\). IRT models are natural fit for Bayesian estimation (Baker & Kim, 2004; Fox, 2010; Lord, 1986; Patz & Junker, 1999) and provide a natural way to obtain ability and item parameter estimates simultaneously.
While ability may be multidimensional or non-normally distributed (Reckase, 2009), it is assumed that \(\theta _i\) is unidimensional and
\begin {equation} \theta _i \sim N(0,1) \end {equation} in this tutorial, for simplicity, as is common in practice. Other common assumptions for IRT models include local independence of responses \begin {equation} P(\pmb {x_i}|\theta _i) = \prod _{j=1}^Jp(x_{ij}|\theta _i) \end {equation} where the probability of observing a given response pattern \(\pmb {x_i}\) is given by \(\pmb {x_i}=(X_{i1}=x_{i1}, ... , X_{iJ}=x_{ij})\) and monotonicity of the latent trait \begin {equation} \theta _1 > \theta _2 \pmb {\rightarrow } p(x=1|\theta _1) \geq p(x=1|\theta _2). \end {equation} Monotonicity implies that higher values of the latent trait increase the probability of endorsing the item. Thus, item scores are typically coded such that all inter-item correlations are nonnegative.
While the distribution of \(\theta \) is often informed by theory underlying constructs of interest or computational convenience, the nature of \(\pmb {\omega }\) depends on item characteristics (e.g., number of response options) and the specified item response model. A common model for binary data is the logistic model (Birnbaum, 1968) which includes a family of models spanning from a single item parameter to four item parameters (Barton & Lord, 1981). These item parameters can accommodate item difficulty, discrimination, and response asymptotes (e.g., guessing). In addition to binary data, many psychological measures contain ordered categorical response options (e.g., Likert-type scales). Polytomous IRT models, such as the graded response model (GRM), are better suited for these instruments (Samejima, 1969). This paper focuses on the two-parameter logistic (2PL) and GRM for binary and ordered categorical responses respectively.
The organization of the rest of the paper is as follows: first, the 2PL and GRM are detailed along with a discussion on priors for item parameters. Then, demonstrations of the 2PL and the GRM in JAGS using the package runjags (Denwood, 2016) are provided using data from the National Longitudinal Survey of Youth (Bureau of Labor Statistics, 2017). Convergence analysis, model fit, and item curves are also demonstrated. We conclude with a brief discussion.
The 2PL model is given by
\begin {equation} P_{ij}(x_j=1|\theta _i,\pmb {\omega }_j)=\frac {\exp (D\alpha _j\theta _i-\beta _K)}{1+\exp (D\alpha _j(\theta _i-\beta _j))} \end {equation} or alternatively \begin {equation} =\frac {1}{1+\exp (-D\alpha _j(\theta _i-\beta _j))} \end {equation} where \(\pmb {\omega }_j = \{\alpha _j,\space \beta _j\}\). Here \(\alpha _j\) is the discrimination parameter, \(\beta _j\) is the difficulty parameter and \(D\) is a scaling constant. The 2PL can also be written as \begin {equation} logit(P_{ij})=D\alpha _j(\theta _i-\beta _j). \end {equation} Since scores can be coded to ensure positive inter-item correlation, which is necessary to preserve the assumption of monotonicity, \(\alpha \)s are constrained greater than 0 and are typically between 0.5 - 2 in practice. The Rasch model can be obtained by constraining \(\alpha _j=1\) (i.e., all items are equally discriminant). No strict constraints are necessary to impose on \(\beta \), however, values of \(\beta \) should overlap with the distribution of \(\theta \) in practice to ensure sufficient variability in item responses. \(D\) is a scaling factor and setting \(D=1.702\) produces essentially the same scaling as the normal ogive model (Camilli, 1994).
Priors for the discrimination parameter \(\alpha _j\) must accommodate the constraint that \(\alpha _j > 0\). Common choices include the truncated normal (i.e., \(N_{+}\), Curtis (2010)) and the lognormal (Patz & Junker, 1999) distributions. We use the truncated normal distribution in the demonstration of the 2PL
\begin {equation} \alpha _j \sim N_+(\mu _{\alpha _j},\sigma ^2_{\alpha _j}). \end {equation} Researchers wishing to use a log-normal prior for \(\alpha _j\) should note that that both \(\mu _{\alpha _j}\) and \(\sigma ^2_{\alpha _j}\) impact the mean and variance of the log-normal distribution making prior specification challenging (Curtis, 2010). We fix \(\phi _{\alpha _j}=1/\sigma ^2_{\alpha _j}=.00001\) and draw \(\mu _{\alpha _j} \sim U[0.5,2]\) in the demonstration below.
The difficulty parameter prior can be specified as a normal distribution
\begin {equation} \beta _j \sim N(\mu _{\beta _j},\sigma ^2_{\beta _j}) \end {equation} allowing the mean (\(\mu _{\beta _j}\)) and variance (\(\sigma ^2_{\beta _j}\)) to vary across items. These parameters can be fixed or treated as hyper-parameters drawn from hyper-priors. For demonstration, we draw \(\mu _{\beta _j} \sim U[-2,2]\) but fix \(\sigma ^2_{\beta _j}\) in the example. We fix \(\sigma ^2_{\beta _j}=10^6\) by fixing the precision of the difficulty parameters \(\phi _{\beta _j} = .000001\). Precision is commonly used in Bayesian analysis and is the inverse of the variance (i.e., \(\phi = 1/\sigma ^2_{\beta _j}\)).
Multiple software programs for Bayesian analysis are openly available (Lunn, Spiegelhalter, Thomas, & Best, 2009; Plummer, 2003; Stan Development Team, 2023). This paper focuses on JAGS implemented in R (R Team Core, 2022) via the runjags package (Denwood, 2016). Alternative packages for running JAGS through R are also available (Plummer, 2022). Specifying models in JAGS consists of three primary components: 1) model specification, 2) initial values, and 3) data. Once all of the components have been compiled, the runjags function can conduct Markov Chain Monte Carlo (MCMC) sampling.
Data for this tutorial consists of 4 items assessing depression in the 2017 wave of the NLSY. For the demonstration of the logistic model, a dichotomized version of the depression items are examined where responses of 1 are recoded as 0 and responses larger than 1 are recoded as a 1. Note that we do not advocate dichotomozing polytomous responses in practice and do this only for pedagogical purposes. Data are provided in the supplementary material.
First we specify twoPL as the 2PL model to run in JAGS. In the code, i indexes the N respondents and j indexes the J items. The item response for person i on item j is represented as \(X[i,j]\) and are drawn from a Bernoulli distribution based on a probability determined by the underlying 2PL.
twoPL<- "
model{
for (i in 1:N){
for (j in 1:J){
X[i, j] ~ dbern(p[i,j])
logit(p[i,j]) <- D*alpha[j]*(theta[i] - beta[j]) #2PL
}
theta[i] ~ dnorm(0, 1)
}
#Priors for model parameters
for (j in 1:J){
beta[j] ~ dnorm(mu.beta[j], pre.beta)
alpha[j] ~ dnorm(mu.alpha[j],pre.alpha)T(0,)
}
#Hyper Prior for mu.beta and mu.alpha
for(j in 1:J){
mu.beta[j] ~ dunif(-1,1)
mu.alpha[j] ~ dunif(.75,1)
}
for(i in 1:N){
for(j in 1:J){
X.rep[i,j] ~ dbern(p[i,j]) #Model implied data
}
}
for(j in 1:J){
ppp[j] <-step(sum(X.rep[,j])-sum(X[,j])) # ppp for item fit
}
D=1.702 #scaling constant
}
"
Here \(\theta _i\) is assumed to follow a standard normal distribution. A normal prior is chosen for difficulty parameters \(\beta _j \sim N(\mu _{\beta _j},\phi _{\beta _j})\), where \(\phi \) is the precision. We draw \(\mu _{\beta _j} \sim U[-2,2]\) and choose \(\phi _{\beta }=.000001\). For the discrimination parameter, a truncated normal (i.e., \(N_+\)) distribution is chosen \(\alpha _j \sim N_+(\mu _{\alpha _j}, \phi _{\alpha _j})\) with \(\mu _{alpha} \sim U[.75,1]\) and \(\phi _{alpha}=.000001\). This prior ensures that \(\alpha _j\) are non-negative. In JAGS, truncation of the normal distribution below at zero is specified using T(0,). In addition to ability and item parameters, X.rep and ppp (i.e., posterior predictive p-values) are specified to obtain posterior predictive checks. X.rep are draws from the implied model to be used in posterior predictive checks via ppp (Gelman, Meng, & Stern, 1996). step(x) is a function which return 1 if \(x \geq 0\) and 0 otherwise.
To calculate the PPP, a new set of data \(\boldsymbol {y^m}\) is generated based on parameter estimate \(\theta ^m\) at MCMC iteration \(m\). The statistic of interest (e.g., expectation) is calculated for both this generated posterior predictive distribution and the sample data \(\boldsymbol {x}\) using \(\theta ^m\). The PPP is the proportion of generated statistics that are greater than the statistics of the data. If \(T\) is the statistics of interest, the PPP can be defined as
\begin {equation} PPP = P(T(\boldsymbol {x}) < T(\boldsymbol {y})). \end {equation} PPP values less than \(0.10\) (i.e., or greater than \(0.90\)) indicate poor fit while models which fit exceptionally well have PPPs near 0.5 (Cain & Zhang, 2019). We choose \(T_j = \sum _{i=1}^N x_{ij}\) for the 2PL and obtain a PPP for each item.
In addition to model specification, it is also necessary to specify initial values for item parameters. When selecting initial parameters, it is crucial to select values of \(\alpha \) and \(\beta \) which are valid for the model (i.e., \(\alpha > 0\)). To specify initial values in JAGS named lists are given for each desired chain. For multiple chains, a list of named lists is used. Below, initial values for 2 chains are specified. Note that for certain convergence metrics, such as the potential scale reduction factor (psrf), multiple chains are needed (Gelman and Rubin (1992)). Additionally, seeds for the Markov chains (i.e., .RNG.seed), as well as the random number generation method (i.e., .RNG.name), can be supplied in the initial values object to make the chains reproducible. JAGS possesses a number of random number generators, we use the Mersenne-Twister method.
inits.2PL <- list(list(beta=rep(-.25, ncol(dep2017.binary)), alpha=rep(.25, ncol(dep2017.binary)), .RNG.seed=1, .RNG.name="base::Mersenne-Twister"), list(beta=rep(.25, ncol(dep2017.binary)), alpha=rep(.5, ncol(dep2017.binary)), .RNG.seed=2, .RNG.name="base::Mersenne-Twister"))
It is also necessary to specify data for JAGS in the form of a named list. This data file includes the item response data as well as other necessary constant values for the model script such as N and J. In the model data list, additional information about the hyperparameters (e.g., precision of \(\alpha \) and \(\beta \)) or model constants (e.g., \(D\)) can be provided if they are not explicitly defined in the model specification. For demonstration, hyperparameter precision is provided as data and the scaling constant \(D\) is defined in the model specification.
data.2PL <- list(N=nrow(dep2017.binary), J=ncol(dep2017.binary), X=dep2017.binary, pre.alpha=1E-6, pre.beta=1E-6)
The run.jags function can be used to translate the model, initial values, and data into JAGS and conduct Gibbs sampling. This function also allows users to specify which model parameters should be monitored for convergence using the monitor argument. In addition to parameters of interest, we are also able to specify other values, such as posterior predictive p-values (PPP), or log-likelihood values to be returned in our output. Users are also able to specify the burnin and chain length using the burnin and sample arguments respectively. Below we specify a burnin period of 1000 samples and a chain length of 3000 samples. For readers new to Bayesian analysis, “burnin” samples are thought to not be sampled prior to Markov Chains to reaching stationarity and are discarded from analysis. JAGS also allows for multiple sampling methods for MCMC via the method argument. We use the parallel method which conducts MCMC sampling for each chain simultaneously on separate cores. The code below conducts sampling in JAGS and returns Markov chains for \(\theta _i\), \(\alpha _j\), \(\beta _j\), and \(ppp_j\). Convergence is evaluated and discussed in a later section.
out.2PL <- run.jags(twoPL,monitor=c("theta","beta","alpha","ppp"),
data=data.2PL, n.chains=2, method="parallel",
inits=inits.2PL,adapt=500, burnin=1000,
sample=3000)
The GRM (Samejima, 1969) is appropriate for items with ordered categorical responses (\(1,...,K_j\)). Note that the number of item response options is allowed to vary by item. It is assumed, however, that response categories are monotonically increasing in difficulty/severity. Then the cumulative probability \(P_{ijk}\) of endorsing up to category \(k\) is
\begin {equation} P_{ijk} = P(X_{ij} \leq k | \theta _i) \end {equation} and the probability \(p_{ijk}\) of endorsing category \(k\) is given by \begin {equation} p_{ijk} = P_{ijk} - P_{ijk-1}, \quad k = 2, ..., K_j \end {equation} with \(p_{ij1} = P_{ij1}\) and \(P_{ijK_j} = 1\). Thus, there are \(K_j-1\) boundaries between response categories governed by item thresholds \(\kappa _1<...<\kappa _{K_j-1}\). Given this, \(P_{ijk}\) can be written as \begin {equation} P_{ijk}(x_{ij} \leq k |\theta _i,\pmb {\omega }_{j}) = \frac {1}{1+\exp (\kappa _{jk}-\alpha _j \theta _i)} \end {equation} Readers will note that (11) is the cumulative distribution of the logistic function similar to the 2PL.
Priors for \(\alpha _j\) can be obtained using the same methods as the 2PL. Again we use the truncated normal distributions \begin {equation} \alpha _j \sim N_{+}(\mu _{\alpha _j},\phi _{\alpha _j}). \end {equation}
Distributions for \(\kappa _j\) need to accommodate the ordering constraint \(\kappa _1<...<\kappa _{K_j-1}\) but otherwise can be conceptualized similar to the \(\beta _j\) parameters in the 2PL. To account for ordering, we recommend using unconstrained auxiliary parameters \(\kappa ^{*}_{j1},...,\kappa ^{*}_{jK_j-1}\) following Curtis (2010). These auxiliary parameters can be drawn from
\begin {equation} \kappa ^{*}_{jk} \sim N(\mu _{\kappa },\sigma ^2_{\kappa }) \end {equation} and sorted in increasing order. Following this rank ordering, \(\kappa _{jk}\) is assigned the \(k\)th ordered \(\kappa ^{*}_{jk}\).
For the GRM, the original Likert-type depression items are analyzed. Responses on the original measure ranged from 1 to 5; however, not all categories were endorsed on each item. Item 1 only has responses in categories \(k = 1,2,3,5\) but items 2-4 have responses to all five categories. While the GRM can easily accommodate different \(K_j\), it is necessary for these categories to be adjacent and start at 1 in JAGS. Thus, responses of \(5\) on item 1 are recoded as \(4\).
The GRM can be specified in JAGS in multiple ways. The first utilizes the categorical distribution for polytomous responses and auxiliary parameters \(\kappa ^{*}\) to obtain item threshold parameters \(\kappa \) (Curtis, 2010). This approach is similar to the 2PL and applies the logit function to each \(p(x_{i,j}=k|\theta _i,\kappa _{j,k},\alpha _j)\) to obtain the probability of responding to each response category. This specification, including a demonstration of the truncated normal distribution for the \(\alpha _j\) prior is provided below.
GRM <- "
model{
for(i in 1:N){
for(j in 1:J){
X[i,j] ~ dcat(prob[i,j,1:K[j]]) #categorical distribution
}
theta[i]~dnorm(0,1)
for(j in 1:J){
for(k in 1:(K[j]-1)){
logit(P[i,j,k])<- kappa[j,k]-alpha[j]*theta[i]
#kappa is the threshold
}
P[i,j,K[j]]<-1
}
for(j in 1:J){
prob[i,j,1] <- P[i,j,1]
for(k in 2:K[j]){
prob[i,j,k] <- P[i,j,k]-P[i,j,k-1]
}
}
}
for(j in 1:J){
#truncated normal prior
alpha[j] ~ dnorm(mu.alpha,pre.alpha)T(0,)
}
for(j in 1:J){
for(k in 1:(K[j]-1)){
#sample auxiliary parameters
kappa.star[j,k] ~ dnorm(mu.kappa,pre.kappa)
}
#Need to sort kappa.star in increasing order
kappa[j,1:(K[j]-1)] <- sort(kappa.star[j,1:(K[j]-1)])
}
pre.alpha = 1E-06 #alpha precision
pre.kappa = 1E-06 #kappa.star precision
mu.alpha = 0.5 #alpha mean
mu.kappa = 0 #kappa.star mean
}
"
This specification also requires a dummy coded data matrix of \(\kappa \) when items possess different number of response categories. This matrix is also \(J\) by \(K-1\) with NA entries where \(\kappa _j\) will be estimated and a dummy value of 0 for entries where no \(\kappa _j\) is to be estimated.
K = apply(dep2017,2,max) #nummber of response categories per item J = ncol(dep2017) #number of items N = nrow(dep2017) #number of respondents kappa.dat = matrix(c(NA,NA,NA,0, NA,NA,NA,NA, NA,NA,NA,NA, NA,NA,NA,NA), nrow=J, ncol=(max(K)-1), byrow=T)
An alternative specification of the GRM uses the ordered logit distribution from the glm module in JAGS. This allows for direct sampling given a location parameter \(\mu \) and sequence of \(K-1\) response categories. For the GRM, the location parameter is given by
\begin {equation} \mu _{i,j} = \alpha _j \theta _i. \end {equation} Readers will note that this specification does not require iteration through the \(K_j-1\) response boundaries. For this reason, we recommend this implementation of the GRM and focus on it for the remainder of this paper.
GRM2 <-"
model{
for(i in 1:N){
for(j in 1:J){
X[i,j]~dordered.logit(mu[i,j],c[j,1:(K[j]-1)])
mu[i,j] <- alpha[j]*theta[i]
}
theta[i]~dnorm(0,1)
}
for(j in 1:J){
for(k in 1:(K[j]-1)){
c[j,k]~dnorm(0,.0001) #prior for thresholds/boundary
}
alpha[j] ~ dnorm(mu.alpha,pre.alpha) #prior for alpha
}
pre.alpha=1E-6
mu.alpha=0
}
"
Specifying initial values of \(\kappa ^{*}\) requires the specification of a \(J\) by \(K-1\) matrix of values. Initial values should be monotonically increasing within each row. Further, for items with less than \(K\) response categories NA should be included as place holder in this matrix. As with the 2PL, initial values for \(\alpha _j\) can be provided in a vector of length \(J\). Both this vector and the matrix for \(\kappa ^{*}\) should be entered into a named list.
kappa.star.init = matrix(c(0,1,2,NA, -1,0,1,2, 0,1,2,3, 0,1,2,3), nrow=J, ncol=max(K)-1, byrow=T) inits.grm = list(list(alpha=rep(1,J), c=kappa.star.init, .RNG.seed=2, .RNG.name="base::Mersenne-Twister"), list(alpha=rep(.5,J), c=kappa.star.init, .RNG.seed=3, .RNG.name="base::Mersenne-Twister"))
In addition to the data directly used in the model, when \(K_j\) differs across items, a matrix for \(\kappa \) (i.e., kappa.dat above) is required for the first implementation of the GRM discussed above. This matrix is not required for the ordered logit approach used here.
data.grm = list(N=N,K=K,J=J, X=as.matrix(dep2017))
MCMC sampling for the GRM is nearly identical to the 2PL. The monitor argument is altered to reflect the new model parameters. The GRM is a more complex model than the 2PL and thus may require more iterations for chains to reach convergence.
out.grm2 <- run.jags(GRM2, monitor=c("c","theta","alpha"),
data=data.grm2, n.chains=2, method="parallel",
inits=inits.grm2, adapt=1000, burnin=10000,
sample=300000, modules="glm")
Following MCMC sampling, it is critical to evaluate if the MCMC procedures converged to a stable posterior distribution that well approximates the underlying process of interest. Convergence analyses, both graphical and statistical, are required to justify the use of resulting chains for inferential purposes. In general it is crucial to determine the stability of the Markov Chains (i.e., convergence to stationarity), the sensitivity of the results to starting values, and the dependence of Monte Carlo samples (i.e., auto-correlation). Below we examine the convergence of the 2PL results obtained above using the coda package (Plummer, Best, Cowles, & Vines, 2006). The same process can be applied to the GRM.
Convergence can be assessed graphically using trace plots and numerically via diagnostic statistics. Multiple diagnostic statistics are available in the coda package including the Geweke Statistic (Geweke, 1992), the Heidelberger and Welch Test (Heidelberger & Welch, 1983), the Raftery and Lewis test (Raftery & Lewis, 1992), and the psrf (Gelman & Rubin, 1992). A review of diagnostic statistics is beyond the scope of this paper and readers are referred to Roy (2020). Below we demonstrate how to examine convergence on a subset of the model parameters; in practice, all parameters for the analysis of interest should be assessed for convergence prior to interpretation and inferential testing.
Multiple plots are helpful in evaluating convergence of posterior distributions. The plot function, when applied to an output from the run.jags function will automatically produce four plots for each paramter monitored during sampling. The plots include the 1) trace plot (i.e. history plot), 2) empirical CDF of the parameter, 3) empirical pdf of the parameter (i.e., historgram), and 4) auto-correlation plot of MCMC samples. Trace plots depict sampled parameter values across the MCMC samples and are useful in cursory evaluation of chain mixing and convergence. Visual evidence of chain convergence is provided when chains appear to stabilize around a single parameter value. Mixed chains demonstrate significant overlap in the trace of each chain. The auto-correlation plot provides insight into the mixing speed of the chains; chains which quickly mix demonstrate small auto-correlation while slower mixing chains possess higher auto-correlation. Empirical cdf and pdf plots allow for direct examination of the posterior distributions itself and allow researchers to check whether posteriors are of the intended form.
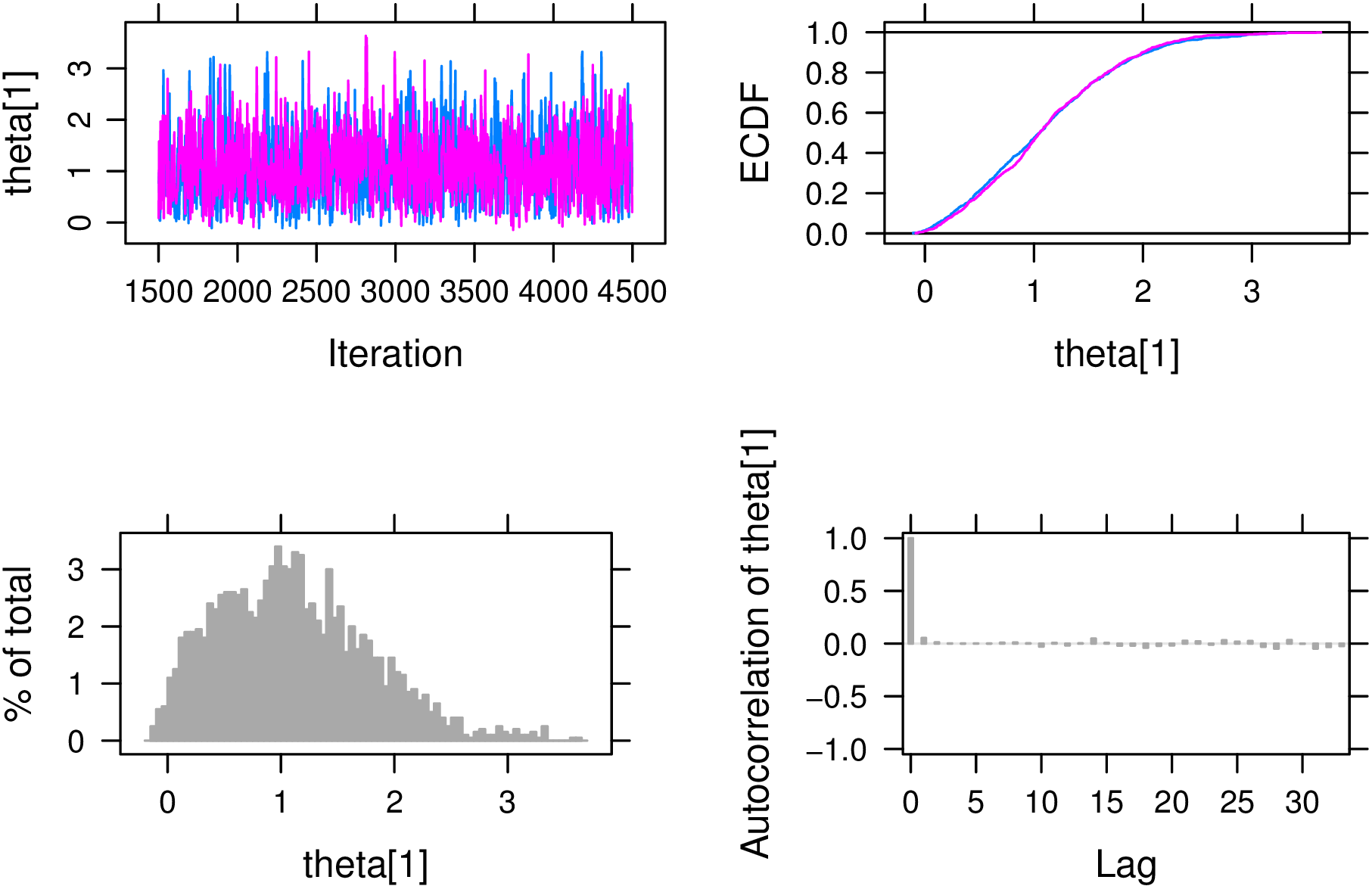
Below plots are provided for a single ability \(\theta _1\) (Figure 1) and difficulty parameter \(\beta _3\) (Figure 2). By default, the plot function will attempt to plot all monitored parameters. To ensure brevity, we specify parameters to plot using the var argument. A brief discussion of each parameter plot is provided below.

The trace plot for \(\theta _1\) is provided in the upper left pane with different colors representing different Markov chains. We see that the chains are largely overlapping and appear to oscillate around a value of \(\theta _1 = 1\) suggesting that the chains have converged to a stationarity posterior distribution. The bottom right pane depicts the auto-correlation plot which shows fast mixing of the two chains. The empirical cdf and pdf of \(\theta _1\), in the top right and bottom left panes respectively, appear to be approximately normal as expected based on assumptions on \(\theta \) and setting \(D=1.702\). Further the empirical cdf is overlapping for both chains.
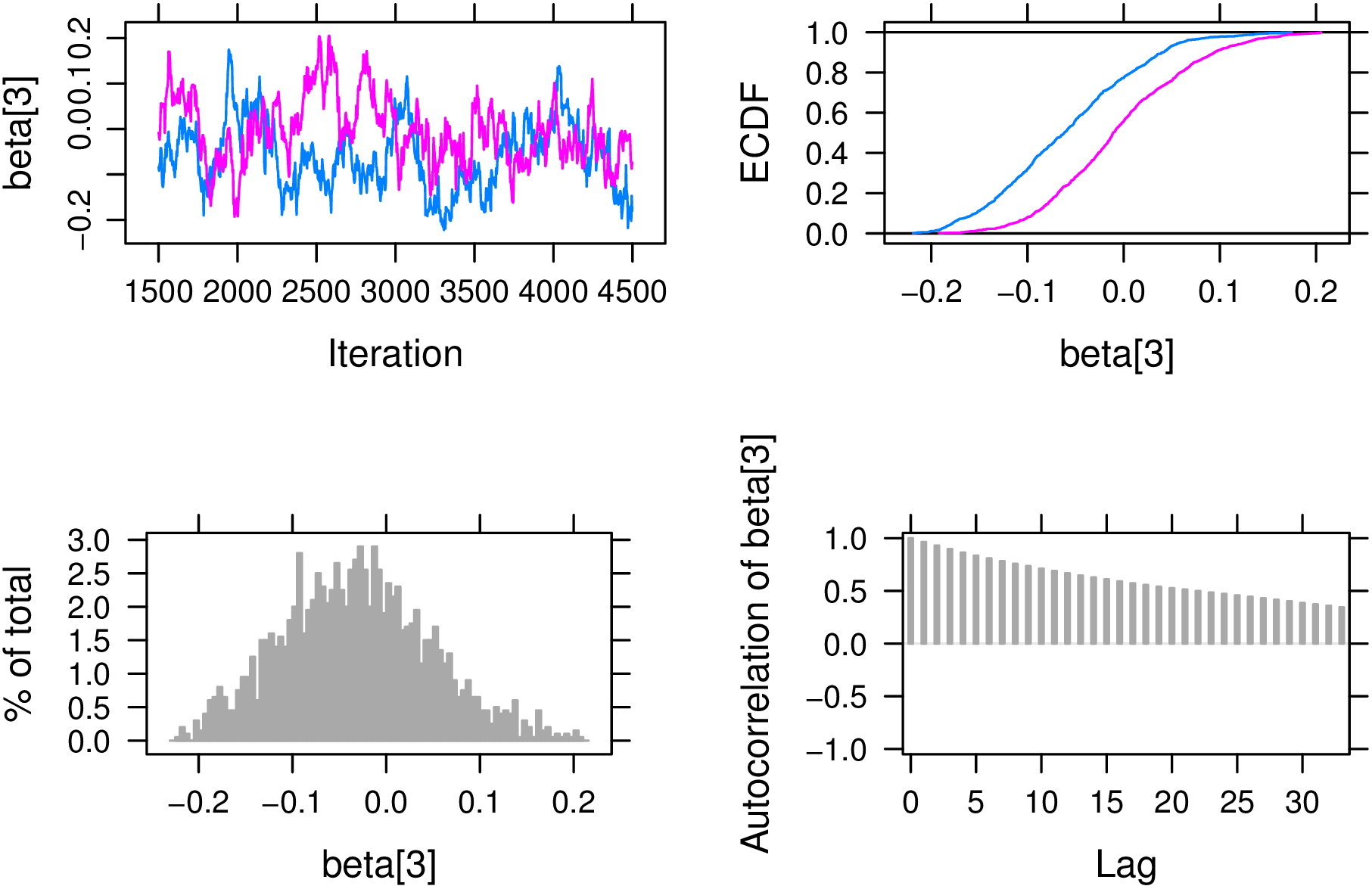
Conversely, the trace plot for \(\beta _3\) shows that chains have neither converged nor mixed well. The auto-correlation plot demonstrates high correlation between samples suggesting a very slow mixing process. Chains do not appear to converge and are mixing very slowly. As a result, it is necessary to increase the chain length and re-run analyses and obtain additional samples.
Although graphical methods of evaluating convergence are useful and intuitive, they are subjective and become impractical when many parameters must be assessed. Thus, it is recommended to evaluate MCMC convergence using numeric metrics as well. We demonstrate how to obtain the Geweke and Gelman Rubin statistics from the coda package.
The Geweke convergence diagnostic tests the equality of means of two segments of a Markov chain with the null hypothesis that the mean of a preliminary segment of the chain (e.g., first 10%) is equal to the latter segment (e.g., last 50%). The Geweke statistic should be applied to individual Markov chains and can be obtained using the geweke.diag function from the coda package. Geweke statistics are Z-scores; values larger than \(\pm 1.96\) suggest a lack of convergence.
chain1 = out.2PL[["mcmc"]][[1]] geweke1 = geweke.diag(chain1)
We show Geweke statistics for the first 4 respondents and all item parameters in the first chain below (Table 1). Here, the Geweke statistics suggest a lack of convergence for \(\theta _1, \space \alpha _1\) and \(\beta _4\) in chain 1. These results suggest that for these chains there is a significant difference between the initial samples in this chain and the later samples. Readers are encouraged to examine the Geweke statistics for all chains as individual chains may reach convergence faster than others.
| theta | alpha | beta |
| -2.446 | 2.031 | -1.797 |
| 1.229 | 0.947 | 0.997 |
| -1.224 | -1.114 | 0.426 |
| -0.254 | 1.394 | 2.165 |
The Gelman and Rubin convergence diagnostic, also denoted as the psrf or rhat, requires multiple Markov chains and can be intuitively understood as a ratio of between chain variance to within chain variance. Values near 1 are preferred and values less than 1.1 are typically used as evidence of chain convergence (Gelman et al., 2015). The gelman.diag function from the coda package calculates point estimates and upper confidence limits of the psrf for each parameter in the chain.
psrf = gelman.diag(out.2PL)
Again, we show psrf diagnostics for the first 4 person parameters as well as the item parameters below (Table 2). Following the pattern from the graphical examination of convergence, \(\theta _i\) appears to show convergence. Convergence for item parameters, however, is less consistent with \(\beta _3\) demonstrating \(psrf > 1.1\). Thus, both graphical and statistical methods suggest that chains are yet to converge.
| theta | alpha | beta |
| 1.006 | 1.000 | 1.024 |
| 1.003 | 1.000 | 1.075 |
| 1.008 | 1.011 | 1.502 |
| 1.010 | 1.005 | 1.018 |
Successful chain convergence is necessary for all model parameters prior to subsequent analysis steps. Without convergence, there is insufficient evidence to support the assumptions that MCMC has reached the stationary posterior distribution needed for inference. Thus, descriptions or inferences drawn from non-convergent Markov Chains are largely invalid. To obtain convergence in the 2PL example, the number of iterations was increased to ensure all \(psrf < 1.10\). The extend.jags function can be used to continue MCMC sampling from an exiting runjags object. Below, we extend the out.2PL object by 1,000,000 iterations. Following this, we confirm that convergence for all parameters has been achieved using the Gelman-Rubin statistic.
out.2PL.ext = extend.jags(out.2PL, method="parallel", sample=1000000, adapt=3000)
Examination of the psrf from the coda package for the longer 2PL chains show convergence in both person and item parameters using \(psrf < 1.1\) as the criteria for convergence. The 5 largest psrf values after extending the chain are provided below.
out.2PL.ext.psrf = gelman.diag(out.2PL.ext) out.2PL.ext.psrf[["psrf"]][order(out.2PL.ext.psrf[["psrf"]][,1], decreasing=TRUE)[1:5],1]
## beta[1] alpha[2] beta[4] beta[3] beta[2] ## 1.010 1.008 1.007 1.002 1.000
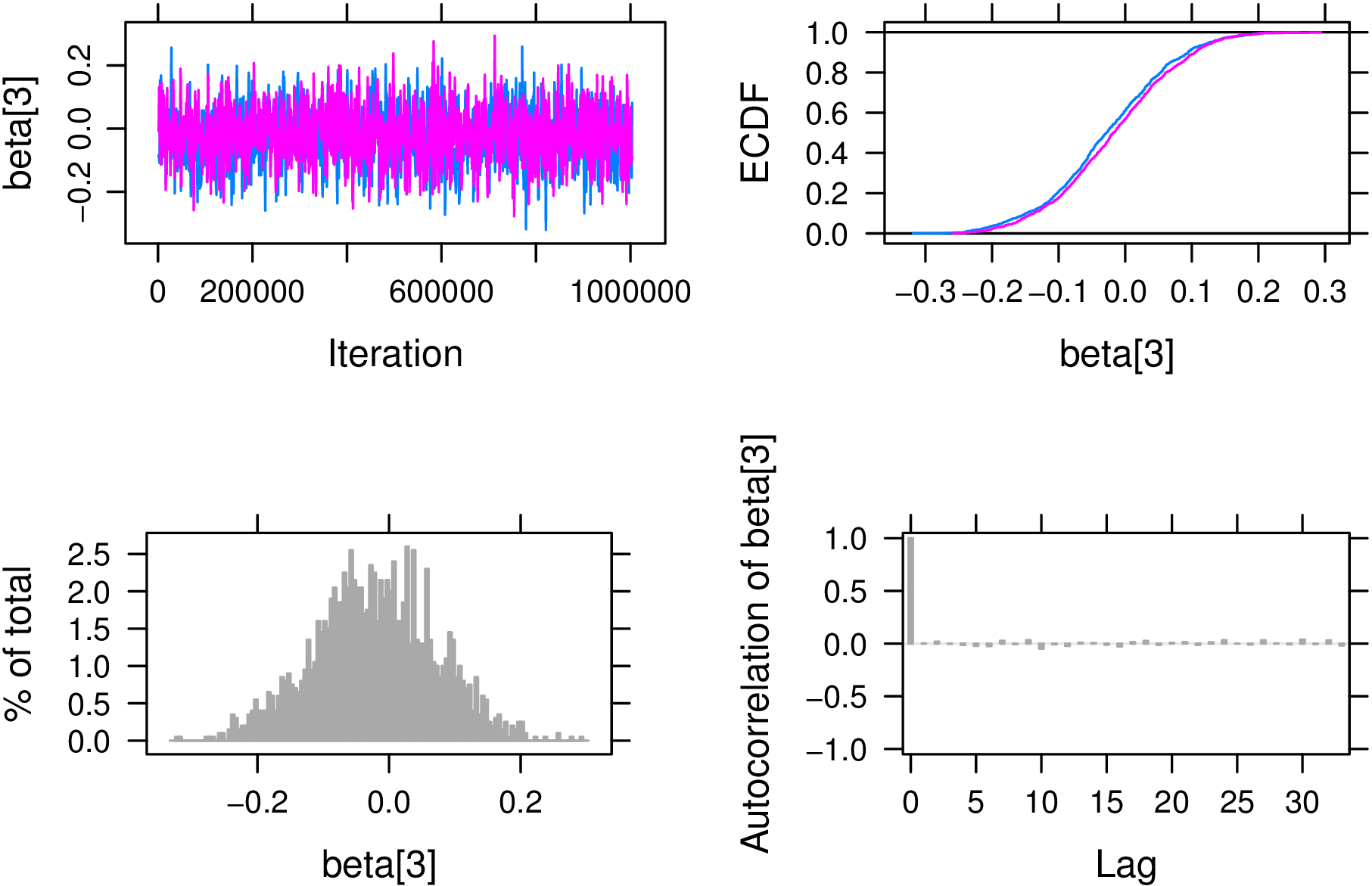
For demonstration, we again provide plots to assess convergence of \(\beta _3\) graphically (Figure 3). Note the overlap of chains in both the trace and empirical CDF plots (i.e., upper left and upper right panes). This is in contrast to the preliminary assessment of convergence above. Additionally, the autocorrelation plot suggests MCMC samples are much closer to independent samples when contrasted with the original convergence plots.
Assessing convergence for the GRM follows the same procedure. Below we observe that the original MCMC did not reach convergence for chain lengths of 300,000 samples.
grm.gelman=gelman.diag(out.grm2) max(grm.gelman[["psrf"]])
For demonstration, we extend the GRM chains using the autoextend.jags function which automatically extends MCMC chains until a target psrf is obtained (e.g., psrf.target=1.10). We see below that our psrf threshold was met. The autoextend.jags function may not work well for complicated models (Denwood, 2016); furthermore, we recommend assessing convergence via the coda package following chain extension to ensure the validity of any subsequent conclusions.
grm.auto = autoextend.jags(out.grm2, psrf.target=1.10, method="parallel") grm.auto.psrf = gelman.diag(grm.auto) max(grm.auto.psrf[["psrf"]][,1]) # < 1.10
## [1] 1.008
Posterior distributions which successfully pass convergence checks can be summarized and, if desired, used for inferential analyses. The runjags package contains a summary function which provides Highest Posterior Density (HPD) intervals, measures of central tendency, and other useful information such as effective sample size (i.e., SSeff). Effective sample size (SSeff) provides a metric of information present in a MCMC accounting for auto-correlation among samples. Recall, however, that samples are correlated and do not provide independent information about the parameter. Effective sample sizes of at least 400 are recommended (Gelman et al., 2015). HPD interval confidence level can be specified using the confidence argument.
For convenience, we split the person parameter (i.e., \(\hat {\theta _i}\)) and item parameter estimates (i.e., \(\hat {\alpha _j}\), \(\hat {\beta _j}\)}) as well as the PPP into separate summary objects. Below we provide example summary output of the summary function for the first 3 \(\theta _i\) parameters.
thetas = summary.2PL[startsWith(rownames(summary.2PL),"theta["),] betas = summary.2PL[startsWith(rownames(summary.2PL),"beta["),] alphas = summary.2PL[startsWith(rownames(summary.2PL),"alpha["),] item.params = rbind(betas,alphas) ppps = summary.2PL[startsWith(rownames(summary.2PL),"ppp["),]
## Lower95 Median Upper95 Mean SD MCerr MC%ofSD SSeff AC.10 psrf ## theta[1] -0.045 1.032 2.414 1.108 0.686 0.003 0.5 40000 0.004 1 ## theta[2] -2.366 -1.046 0.000 -1.119 0.658 0.003 0.5 39310 0.004 1 ## theta[3] -0.093 0.718 1.975 0.812 0.586 0.003 0.5 40000 0.010 1
Posterior distributions of \(\theta _i\) and HPD intervals can be used to compare ability/severity across individual respondents. Below (Figure 4), 95% HPD intervals of \(\hat {\theta _i}\) are plotted for \(\theta _i\). It is readily seen that although individuals vary in their point estimates of depression, the interval estimates largely overlap. HPDs are gplotted for both the 2PL and the converged GRM (code provided in supplemental material). Notice that HDIs for the 2PL are much larger in this example which is partially attributable to dichotomizing ordinal response options. Additionally, note that \(\theta _i\) HPD intervals in the GRM centered above \(\theta _i=1\) posses narrower intervals which is a function of item information discussed in a subsequent section.
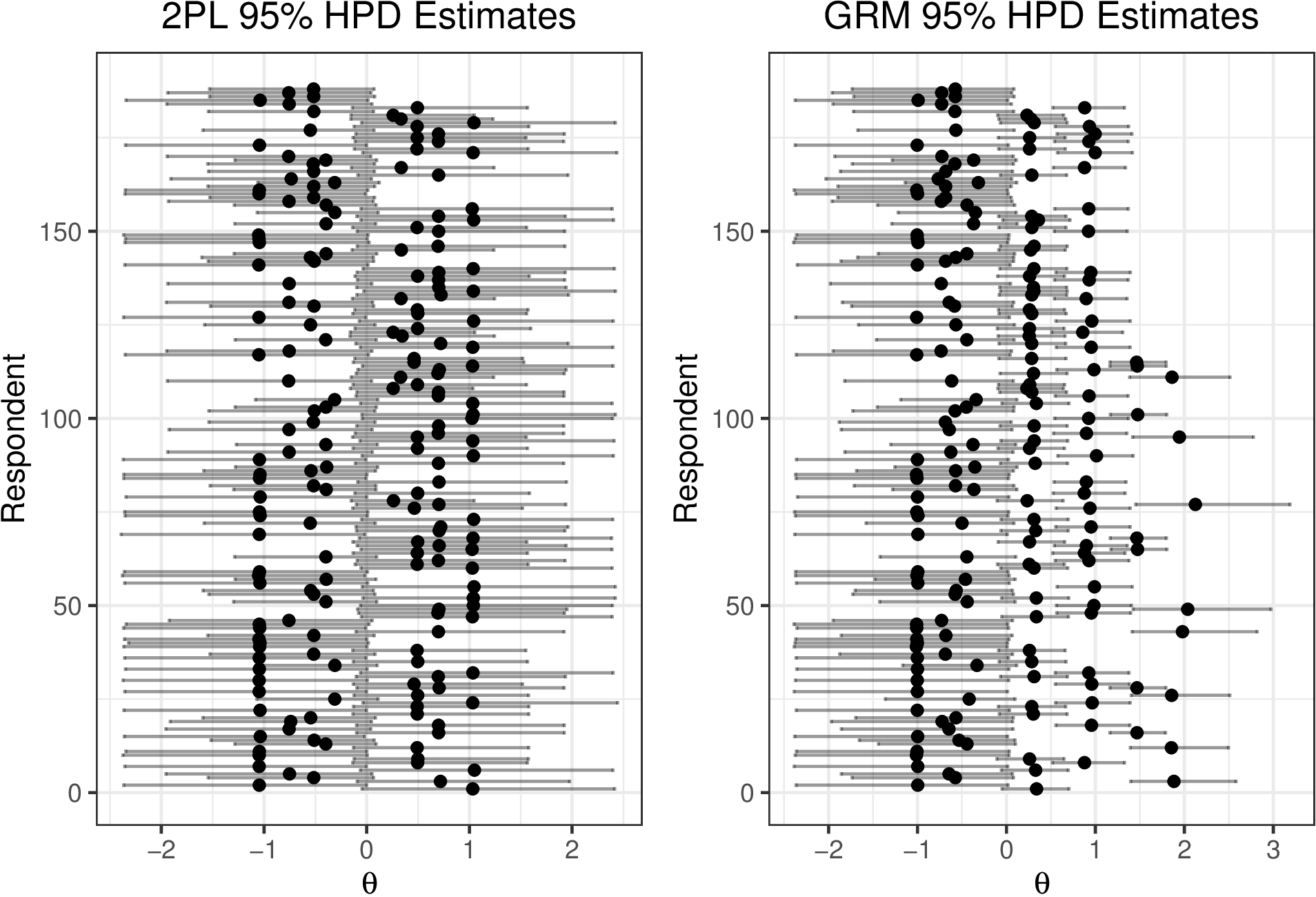
Here we see that the 2PL and the GRM yield similar \(\hat {\theta }\) estimates; however, the intervals for the GRM are typically much narrower. This reflects the increased precision in estimates that arises from preserving the original ordinal scale of the items rather than dichotomizing it as was done for 2PL demonstration. Further, it is worth noting that the width of the HPD varies based on the \(\hat {\theta }\) with estimates larger than zero demonstrating relatively more precision. This suggests that these particular items may be better at distinguishing among respondents with mild to moderate levels of depression than their non-depressed counterparts.
Posterior predictive checks can be used to determine if the proposed models fit the observed data. We use the PPP (Gelman et al., 1996). We observe that \(PPP \approx 0.50\) for items 1,2 and 4 but \(ppp_{3} = 0.9\) suggesting that the the 2PL is a reasonable model for items 1,2, and 4 does not perform well for item 3. PPPs could also be obtained for each respondent to detect potential outlying response patterns by altering the JAGS model specification to include PPPs for each \(i\). We can use the posterior mean of the \(PPP_j\) to examine model fit for each item.
## ppp[1] ppp[2] ppp[3] ppp[4] ## 0.516 0.532 0.903 0.524
It is often of interest when conducting IRT analyses to evaluate how well test items perform across a range of \(\theta \)s. For example, certain items may be more informative for respondents with high levels of \(\theta \) while other perform better at lower levels. In this section we demonstrate how to plot Item Characteristic Curves (ICCs), Item Information Curves (IICs), and test information for the 2PL. Given the poor model fit for item 3, we only examine curves for items 1, 2, and 4. We use the posterior means of all item and person parameters to compute \(p_{ij}\).
alpha_hat = alphas[c(1,2,4),"Mean"]
beta_hat = betas[c(1,2,4),"Mean"]
theta_hat = thetas[,"Mean"]
p = calcP(thet=theta_hat,a=alpha_hat,b=beta_hat,D=1.702)
colnames(p) <- paste0("Item",c(1,2,4))
Researchers often wish to examine how the probability of endorsing (or correctly answering) an item varies as a function of \(\theta \). ICCs plot \(p_j\) across the range of \(\theta \) providing a useful description of item functioning. Figure 5 plots \(p_{ij}\) over \(\hat {\theta }\) for items 1, 2, and 4.
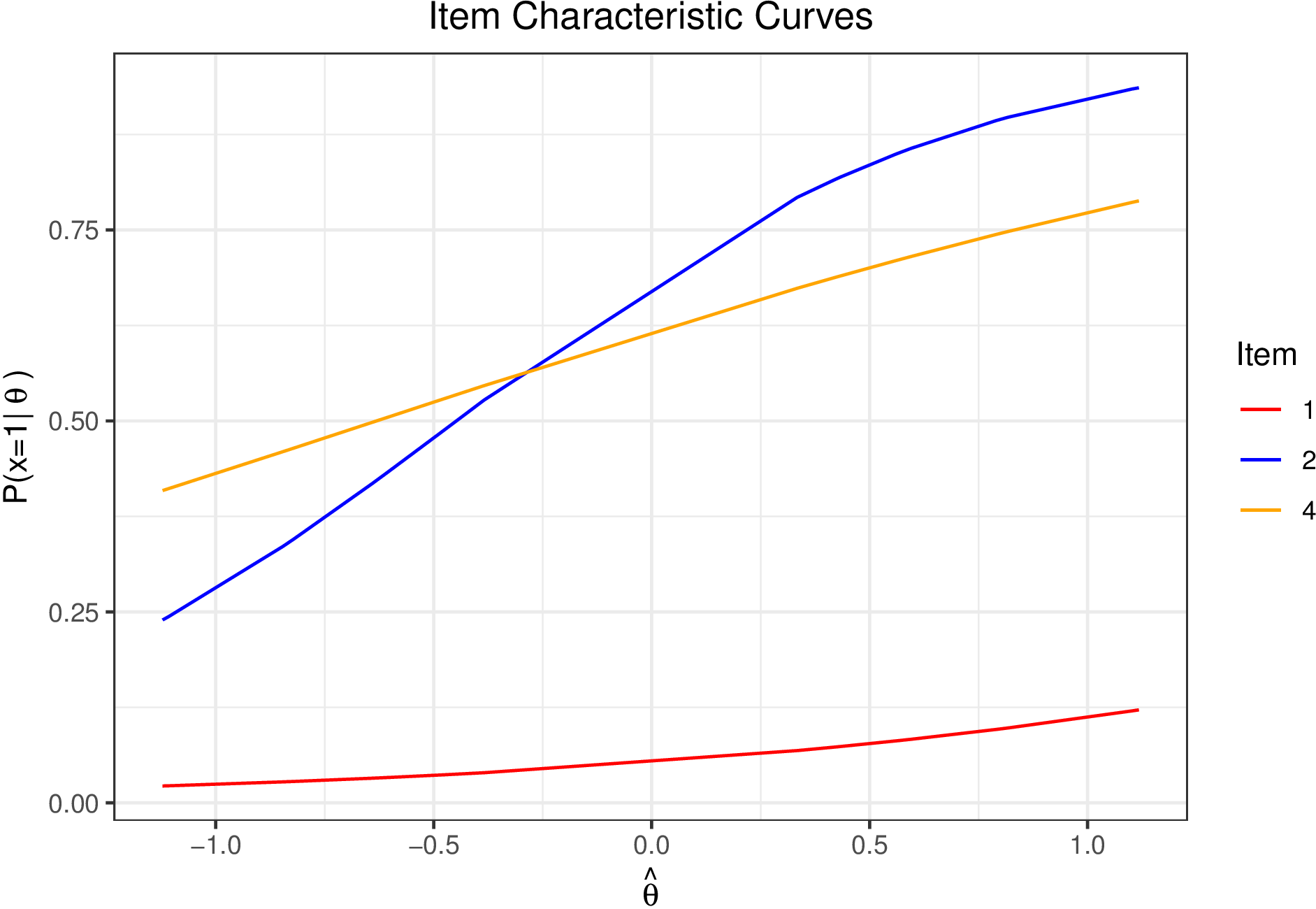
The ICC demonstrates that item 1 is rarely ever endorsed across the \(\theta \) range. The remaining items are endorsed more frequently as \(\theta \) increases (i.e., more severe depression).
It is also often helpful to plot the item information curves (IIC) which depict how informative responses to an item are for a given level of ability. Items are often evaluated using Fisher information which is defined for the 2PL (Lord, 1980)
\begin {equation} I(\theta ,x_j) = \alpha _j^2p_{ij}(1-p_{ij}). \end {equation} Fixing \(\alpha _j\) to be the posterior mean as above, we can obtain item information curves. Figure 6 displays the item information for Items 1, 2, and 4.
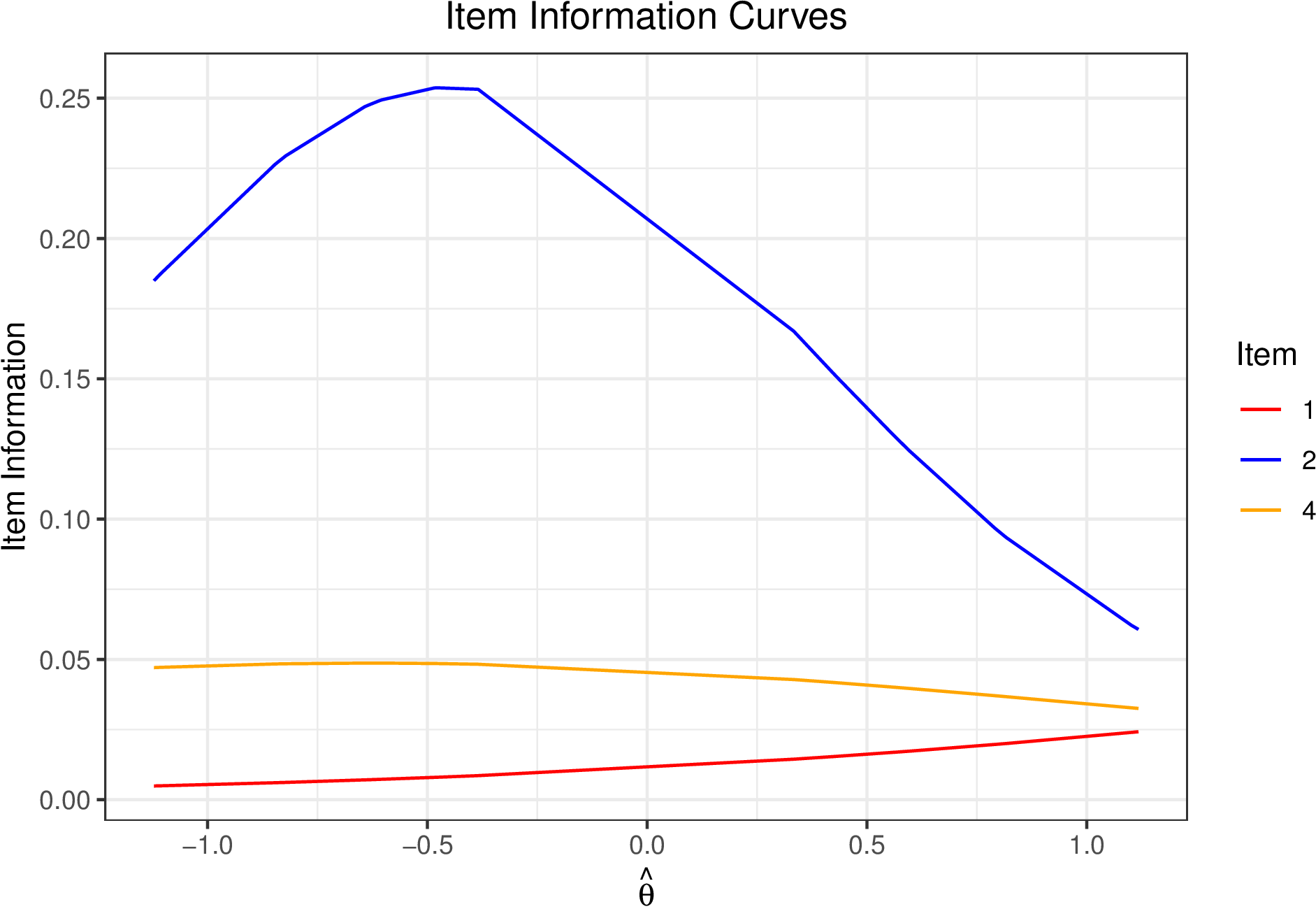
Item information provides a metric for how well an item performs across values of \(\theta \). The test information provides a similar metric for the entire test. Given the assumption of local independence, calculating test information is a straightforward sum of the item information. Below we demonstrate how to plot the overall test information again omitting item 3 (Figure 7).

This paper provides a demonstration of Bayesian IRT models, specifically the 2PL and GRM, in JAGS using the runjags package. The general procedure for conducting Bayesian analyses can be summarized in 7 overarching steps:
Details of each step clearly varies based on models and analytic but this general template provides a heuristic for conducting Bayesian IRT analyses using JAGS. Code to implement the 2PL and GRM as well as conduct convergence diagnostics and summarize posterior MCMC is provided.
This paper provided a demonstration of Bayesian IRT models via the 2PL and GRM in JAGS using data from the NLSY. In general, implementing models in JAGS requires 1) Model specification including priors, 2) specification of initial values, and 3) specifying the data needed to run the model. Depending on idiosyncracies of item response models, dummy coded data for certain parameters, such as the item intercepts in the GRM examined here, may be necessary in JAGS. The models demonstrated here are by no means exhaustive of item response models that can be analyzed in JAGS but provide a foundation for readers to understand the general process of implementing IRT models in JAGS and evaluating model convergence.
Baker, F. B., & Kim, S.-H. (2004). Item response theory: Parameter estimation techniques (Second ed.). Boca Raton: CRC Press. doi: https://doi.org/10.1201/9781482276725
Barton, M. A., & Lord, F. M. (1981). An upper asymptote for the three-parameter logistic item-response model. ETS Research Report Series, 1981(1), i–8. doi: https://doi.org/10.1002/j.2333-8504.1981.tb01255.x
Birnbaum, A. (1968). Some latent trait models and their use in inferring an examinee’s ability. In F. Lord & M. Novick (Eds.), Statistical theories of mental test scores (pp. 397–479). Reading: Addison-Wesley.
Bureau of Labor Statistics. (2017). National Longitudinal Survey of Youth 1997 cohort, 1997-2017 (rounds 1-18).
Cain, M. K., & Zhang, Z. (2019). Fit for a bayesian: An evaluation of ppp and dic for structural equation modeling. Structural Equation Modeling: A Multidisciplinary Journal, 26(1), 39–50. doi: https://doi.org/10.1080/10705511.2018.1490648
Camilli, G. (1994). Teacher’s corner: Origin of the scaling constant d = 1.7 in item response theory. Journal of Educational Statistics, 19(3), 293–295. doi: https://doi.org/10.3102/10769986019003293
Curtis, S. M. (2010, August). BUGS code for item response theory. Journal of Statistical Software, 36, 1–34. doi: https://doi.org/10.18637/jss.v036.c01
Denwood, M. J. (2016). Runjags: An R package providing interface utilities, model templates, parallel computing methods and additional distributions for MCMC models in JAGS. Journal of statistical software, 71, 1–25. doi: https://doi.org/10.18637/jss.v071.i09
Embretson, S. E., & Reise, S. P. (2000). Item response theory for psychologists. Mahwah, NJ, US: Lawrence Erlbaum Associates Publishers.
Fox, J.-P. (2010). Bayesian item response modeling: Theory and applications. New York, NY: Springer. doi: https://doi.org/10.1007/978-1-4419-0742-4
Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2015). Bayesian Data Analysis (Third ed.). New York: Chapman and Hall/CRC. doi: https://doi.org/10.1201/b16018
Gelman, A., Meng, X.-L., & Stern, H. (1996). Posterior predictive assessment of model fitness via realized discrepancies. Statistica sinica, 6(4), 733–760.
Gelman, A., & Rubin, D. B. (1992). Inference from iterative simulation using multiple sequences. Statistical Science, 7(4), 457–472.
Geweke, J. (1992). Evaluating the accuracy of sampling-based approaches to the calculations of posterior moments. Bayesian Statistics, 4, 641–649. doi: https://doi.org/10.21034/sr.148
Heidelberger, P., & Welch, P. D. (1983). Simulation run length control in the presence of an initial transient. Operations Research, 31(6), 1109–1144. doi: https://doi.org/10.1287/opre.31.6.1109
Lord, F. M. (1980). Applications of item response theory to practical testing problems. New York: Routledge. doi: https://doi.org/10.4324/9780203056615
Lord, F. M. (1986). Maximum likelihood and bayesian parameter estimation in item response theory. Journal of Educational Measurement, 23(2), 157–162. doi: https://doi.org/10.1111/j.1745-3984.1986.tb00241.x
Lunn, D., Spiegelhalter, D., Thomas, A., & Best, N. (2009). The BUGS project: Evolution, critique and future directions. Statistics in Medicine, 28(25), 3049–3067. doi: https://doi.org/10.1002/sim.3680
Patz, R. J., & Junker, B. W. (1999). A straightforward approach to Markov Chain Monte Carlo methods for item response models. Journal of Educational and Behavioral Statistics, 24(2), 146–178. doi: https://doi.org/10.2307/1165199
Plummer, M. (2003). JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. In K. Hornik, F. Leisch, & A. Zeileis (Eds.), Proceedings of the 3rd international workshop on distributed statistical computing.
Plummer, M. (2022). Rjags: Bayesian graphical models using MCMC [Manual].
Plummer, M., Best, N., Cowles, K., & Vines, K. (2006, March). CODA: Convergence diagnosis and output analysis for MCMC. R News, 6(1), 7–11.
R Team Core. (2022). R: A language and environment for statistical computing [Computer software manual]. Vienna, Austria.
Raftery, A. E., & Lewis, S. M. (1992). Practical Markov Chain Monte Carlo: Comment: One long run with diagnostics: Implementation strategies for Markov Chain Monte Carlo. Statistical Science, 7(4), 493–497. doi: https://doi.org/10.1214/ss/1177011143
Reckase, M. (2009). Multidimensional item response theory. New York, NY: Springer. doi: https://doi.org/10.1007/978-0-387-89976-3
Roy, V. (2020). Convergence diagnostics for Markov chain Monte Carlo. Annual Review of Statistics and Its Application, 7, 387–412. doi: https://doi.org/10.1146/annurev-statistics-031219-041300
Samejima, F. (1969). Estimation of latent ability using a response pattern of graded scores. Psychometrika Monograph Supplement, 34(4), 100–100. doi: https://doi.org/10.1007/bf03372160
Stan Development Team. (2023). RStan: the R interface to Stan. Retrieved from https://mc-stan.org/ (R package version 2.21.8)
NLSY Depression Items:
dep2017.binary <- apply(dep2017,2,function(x){ifelse(x>1,1,0)})
dep2017[dep2017[,1]==5,1]<-4
summary.theta.df = data.frame(thetas)
summary.theta.df$id <- 1:nrow(thetas)
hpd1 <- ggplot(data=summary.theta.df,aes(y=id))+
geom_point(aes(x=Median))+
geom_errorbar(aes(xmin=Lower95,xmax=Upper95),alpha=.4)+
ylab("Respondent")+
xlab(expression(theta))+
ggtitle("2PL 95% HPD Estimates")+
theme_bw()+theme(plot.title=element_text(hjust=.5))
summary.thetas.grm.df = data.frame(thetas.grm)
summary.thetas.grm.df$id <- 1:nrow(thetas.grm)
hpd2 <- ggplot(data=summary.thetas.grm.df,aes(y=id))+
geom_point(aes(x=Median))+
geom_errorbar(aes(xmin=Lower95,xmax=Upper95),alpha=.4)+
ylab("Respondent")+xlab(expression(theta))+
ggtitle("GRM 95% HPD Estimates")+theme_bw()+
theme(plot.title=element_text(hjust=.5))
# Calculate probability of x = 1 given theta, alpha, beta
calcP <- function(theta,a,b,D=1.702){ #D is scaling constant
logitP = D*(a%*%t(theta)-b)
p = exp(logitP)/(1+exp(logitP))
return(t(p))
}
# Item Characteristic Curves
ICC.df = data.frame(theta=theta_hat,p)
ICC.plot <- ggplot(ICC.df,aes(x=theta))+
geom_line(aes(y=Item1,color=’1’))+
geom_line(aes(y=Item2,color=’2’))+
geom_line(aes(y=Item4,color=’3’))+
xlab(expression(hat(theta)))+
ylab(expression("P(x=1|"~theta~")"))+ggtitle("ICC Plot")+
scale_color_manual(name="Item",breaks=c("1","2","3"),
values=c("1"="red","2"="blue","3"="orange"),
labels=c("1","2","4"))+
theme_bw()+theme(plot.title=element_text(hjust=.5))
# Item Information Curve
IIC.df = data.frame(I.item1 = alpha_hat[1]^2*(p[,1]*(1-p[,1])),
I.item2 = alpha_hat[2]^2*(p[,2]*(1-p[,2])),
I.item4 = alpha_hat[3]^2*(p[,3]*(1-p[,3])),
theta_hat)
IIC.plot <- ggplot(IIC.df,aes(x=theta_hat))+
geom_line(aes(y=I.item1,color=’1’))+
geom_line(aes(y=I.item2,color=’2’))+
geom_line(aes(y=I.item4,color=’3’))+
xlab(expression(hat(theta)))+
ylab("Item Information")+ggtitle("Item Information Plot")+
scale_color_manual(name="Item",breaks=c("1","2","3"),
values=c("1"="red","2"="blue","3"="orange"),
labels=c("1","2","4"))+
theme_bw()+theme(plot.title=element_text(hjust=.5))
# Test Information Curve
test.i.df = data.frame(theta_hat,
testInfo=apply(IIC.df[,1:3],1,sum))
test.i.plot <- ggplot(test.i.df,aes(x=theta_hat))+
geom_line(aes(y=testInfo))+
ylab("Test Information")+xlab(expression(theta))+
xlab(expression(hat(theta)))+
ggtitle("Test Information Curve")+
theme_bw()+theme(plot.title=element_text(hjust=.5))