Keywords: Meta-analysis of proportions · Heterogeneity · Meta-regression · Double arcsine transformation · Baujat plot
A meta-analysis is a statistical approach that synthesizes quantitative findings from multiple studies investigating the same research topic. Its purpose is to provide a numerical summary of a particular research area, aiming to inform future work in that area. Meta-analyses of proportions are commonly conducted across diverse scientific fields, such as medicine (e.g., Gillen, Schuster, Meyer Zum Bschenfelde, Friess, & Kleeff, 2010), clinical psychology (e.g., Fusar-Poli et al., 2015), epidemiology (e.g., Wu, Long, Lin, & Liu, 2016), and public health (e.g., Keithlin, Sargeant, Thomas, & Fazil, 2014), etc. The outcomes derived from these studies are often used for decision models (Hunter et al., 2014). Each individual study included in a meta-analysis of proportions contributes a specific number of “successes” and a corresponding total sample size (Hamza, van Houwelingen, & Stijnen, 2008). While the majority of meta-analyses primarily focus on effect-size metrics that measure a relationship between a treatment group and a control group–such as standardized mean difference and odds ratio–the effect-size metric in meta-analyses of proportions is an estimate of the overall proportion related to a particular condition or event across all included studies (Barendregt, Doi, Lee, Norman, & Vos, 2013). For instance, a meta-analysis can be conducted to provide an overall prevalence estimate of homeless veterans affected by both post-traumatic stress disorder and substance use disorder.
The purpose of this tutorial is to provide an introduction to conducting a meta-analysis of proportions using the R software (R Core Team, 2022). We discuss two distinct benefits of choosing R as your primary meta-analysis tool. First, R is freely available open-source software that offers a comprehensive collection of R packages, which are extensions developed for specialized applications, including meta-analysis. This remarkable feature provides researchers with diverse possibilities and flexibility when it comes to data manipulation and analysis. Two widely used R packages for meta-analysis are metafor (Viechtbauer, 2010) and meta (Schwarzer, Carpenter, & Rücker, 2015). Second, R offers more convenient options for transforming proportional data than other statistical software. The two commonly adopted data transformation methods are the logit and the double arcsine transformations (though not transforming data is also appropriate under certain circumstances). Both the metafor and meta packages are capable of performing these transformations. In contrast, other meta-analysis software such as Comprehensive Meta-Analysis (CMA) (Borenstein, Hedges, Higgins, & Rothstein, 2005) and MedCalc (Schoonjans, 2017) can only perform one of these transformations. Additionally, while CMA and MedCalc automatically transform data, R allows meta-analysts to make a decision on whether to apply data transformation.
To the best of our knowledge, this is the first tutorial that illustrates the implementation of such analyses. The tutorial offers an overview of the fundamental statistical concepts related to meta-analysis of proportions and provides hands-on code examples to guide readers through the process in R.1 We use a dataset from a published meta-analytic study to detail the steps involved. Moreover, we’ve rigorously tested the code in R and validated it using CMA, ensuring identical results from both software.
Last but not least, this tutorial will explain why common publication bias assessment procedures aren’t recommended for meta-analyses of proportions.
The first step is to download R. The base R program can be downloaded for free from the Comprehensive R Archive Network (https://cran.r-project.org/). R provides a basic graphical user interface (GUI), but we recommend that readers use a more productive code editor that interfaces with R, known as RStudio (RStudio Team, 2022). This is a development environment built to make using R as effective and efficient as possible, which is freely available at https://www.rstudio.com/. It adds much more functionality above and beyond R’s bare-bones GUI.
Once RStudio is successfully installed on your computer and opened, the first step is to create a new R Script. To do this, navigate to the “File” menu. Click on “File”, and in the dropdown menu, select “New File”, then choose “R Script”. A new tab will open in the top-left pane of RStudio, known as the source editor. This space is where you’ll write your R code.
To ensure proper organization of your R files and data, it’s crucial to establish a working directory for the current R session. A working directory serves as a centralized location where you can store all your work, including the R code you’ve written and data files (e.g., .csv files) you wish to import into R for analysis. To set up a working directory, start by creating a folder named “data” in your preferred location on the computer, such as the D drive. After doing so, enter the following code into the source editor:
setwd("D:/data")
The data set we will use for this tutorial is extracted from a published meta-analytic study conducted by Wu et al. (2016). They estimated the prevalence of congenital cataracts (CC) and their main epidemiological traits. CC refers to the opacity of the lens detected at birth or at an early stage of childhood. It is the primary cause of treatable childhood blindness worldwide. Current studies have not determined the etiology of this condition. The few large-scale epidemiological studies on CC also have limitations: they involve specific regions, limited populations, and partial epidemiological variables. Wu et al. (2016) aimed to explore its etiology and estimate its population-based prevalence and major epidemiological characteristics, morphology, associated comorbidities and etiology. The original dataset consists of 27 published studies that were published from 1983 to 2014, among which 17 contained data on the population-based prevalence of CC, 2 were hospital-based studies and 8 were CC-based case reviews. Samples investigated in the studies were from different regions of the world, including Europe, Asia, the USA, Africa, and Australia. The sample sizes of the included studies ranged from 76 to 2,616,439 patients, with a combined total of 8,302,708 patients. The diagnosed age ranged from 0 to 18 years of age. The proportions were transformed using the logit transformation, which is commonly employed when dealing with proportional data. This transformation results in a sampling distribution that is more normal, with a mean of zero and a standard deviation of 1.83. The authors coded five moderators, including world region (China vs. the rest of the world), study design (birth cohort vs. other), sample size (less vs. more than 100,000), diagnosed age (older vs. younger than 1 year old), and research period (before vs. after the year 2000). All of these potential moderators are categorical variables. Due to page limits, we will work with only a subset of the provided moderating variables, including study design and sample size.
Prior to performing a meta-analysis in R, it is important to first organize the data properly. Table 1 shows an excerpt of the example dataset. Each row in this table represents the data extracted from a primary study included in the current meta-analysis. The columns contain variables that will be used to compute effect sizes, create plots, and conduct further analyses.
| author | year | authoryear | cases | total | studesg | studydesign | size | samplesize |
| Stewart-Brown | 1988 | Stewart-Brown 1988 | 7 | 12853 | 0 | Birth cohort | 0 | \(<\) 100000 |
| Bermejo | 1998 | Bermejo 1998 | 71 | 1124654 | 0 | Birth cohort | 1 | \(>\) 100000 |
| SanGiovanni | 2002 | SanGiovanni 2002 | 73 | 53639 | 0 | Birth cohort | 0 | \(<\) 100000 |
| Haargaard | 2004 | Haargaard 2004 | 773 | 2616439 | 0 | Birth cohort | 1 | \(>\) 100000 |
| Stayte | 1993 | Stayte 1993 | 4 | 6687 | 0 | Birth cohort | 0 | \(<\) 100000 |
| Stoll | 1997 | Stoll 1997 | 57 | 212479 | 0 | Birth cohort | 1 | \(>\) 100000 |
| Rahi | 2001 | Rahi 2001 | 248 | 734000 | 1 | Others | 1 | \(>\) 100000 |
| Wirth | 2002 | Wirth 2002 | 421 | 1870000 | 1 | Others | 1 | \(>\) 100000 |
| Hu | 1987 | Hu 1987 | 77 | 207319 | 1 | Others | 1 | \(>\) 100000 |
| Abrahamsson | 1999 | Abrahamsson 1999 | 136 | 377334 | 1 | Others | 1 | \(>\) 100000 |
| Bhatti | 2003 | Bhatti 2003 | 199 | 982128 | 1 | Others | 1 | \(>\) 100000 |
| Nie | 2008 | Nie 2008 | 15 | 15398 | 1 | Others | 0 | \(<\) 100000 |
| Chen | 2014 | Chen 2014 | 6 | 9246 | 1 | Others | 0 | \(<\) 100000 |
| Yang | 2014 | Yang 2014 | 8 | 6299 | 1 | Others | 0 | \(<\) 100000 |
| Pi | 2012 | Pi 2012 | 3 | 3079 | 1 | Others | 0 | \(<\) 100000 |
| Holmes | 2003 | Holmes 2003 | 10 | 33021 | 1 | Others | 0 | \(<\) 100000 |
| Halilbasic | 2014 | Halilbasic 2014 | 51 | 38133 | 1 | Others | 0 | \(<\) 100000 |
In this data set, we have separate columns for authors’ names and the year of publication, which will be useful when sorting studies according to the year of publication in R. Additionally, if we decide to use the forest() function in the meta package to create forest plots, we need to create a column that combines both variables. In this case, we label the column as “authoryear”. It’s important to note that when importing a data file into R, column names with uppercase letters will be converted to lowercase. Therefore, we cannot use uppercase or lowercase letters to differentiate between different columns. Moreover, we cannot leave a blank space between two words when naming a column. As seen in the table, we use “authoryear” instead of “author year”, “studydesign” instead of “study design”, and “samplesize” instead of “sample size”.
The variable “cases” represents the number of the event of interest in the sample of each study. By dividing “cases” by “total”, we can obtain the proportions needed to compute effect sizes, which are labeled as “yi” in R. R will also calculate the sampling variance for each “yi” and label them as “vi”. The remaining variables in the dataset are potential moderators, which will be examined in either a subgroup analysis or a meta-regression. For instance, “study design” is a potential moderator with two categories or levels: “birth cohort” and “others”. We have coded each category as either 1 or 0 in the column labeled “studesg”. For continuous moderators, readers can create columns to store continuous values, such as the “year” column. This dataset is saved as a comma-separated values (.csv) file named “data.csv” and is included in the online supplemental materials for this tutorial. To import it into R, ensure the .csv file is stored in the working directory.
Before combining effect sizes in a meta-analysis, we need to make a choice between two modeling approaches for calculating the summary effect size:2 the fixed-effect and random-effects model (Hedges & Vevea, 1998; Hunter & Schmidt, 2000). The fixed-effect model assumes that studies included in a meta-analysis are functionally equivalent, sharing a common true effect size. Put differently, the true effect size is identical across studies, and any observed variation in effect size estimates is solely due to random sampling error within each study, known as within-study variance. The random-effects model allows the included studies to have true effect sizes that are not identical or “fixed” but follow a normal distribution. In other words, the random-effects model accounts for both within-study and between-study variances, while the fixed-effect model assumes that the between-study variance is zero (i.e., between-study heterogeneity does not exist).
The fixed-effect model applies when participants in the studies are drawn from a single common population and undergo the same experimental procedures conducted by the same researchers under identical conditions. For instance, a series of studies with the same protocol conducted in the same lab and sampling from the same population (e.g., school children from the same class) may fit the fixed-effect model. However, these conditions rarely hold in reality. In fact, the majority of meta-analyses are conducted based on studies collected from the literature. In such cases, we can generally assume that the true effect varies from study to study. Even when a group of studies focuses on a common topic, they are often conducted using different methods (Borenstein, 2019). Consequently, the true effect size is assumed to follow a normal distribution under the random-effects model.
An additional limitation of the fixed-effect model is that its conclusions are limited to the specific set of studies included in the meta-analysis and cannot be generalized to multiple populations. However, most social scientists aim to make inferences that extend beyond the selected set of studies in their meta-analyses. As a general rule of thumb, the random-effects model will be more plausible than the fixed-effect model in most meta-analytic studies because the random-effects model allows more generalizable conclusions beyond a specific population (Borenstein, 2019; Borenstein, Hedges, Higgins, & Rothstein, 2009). However, we discourage the practice of switching to the random-effects model from the fixed-effect model based solely on the results of heterogeneity tests. We will discuss the reasons in more depth later.
The random-effects model can be estimated by several methods (although other methods exist, we will focus on the most popular ones here): the method of moments or the DerSimonian and Laird method (DL; DerSimonian & Laird, 1986) and the restricted maximum likelihood method (REML; Raudenbush & Bryk, 1985). In all cases, the summary effect size (i.e., the summary proportion) is estimated as the weighted average of the observed effect sizes extracted from primary studies. The weighting for each observed effect size is the inverse of the total variance of a study, which is the sum of the within-study variance and the between-study variance (Ma, Chu, & Mazumdar, 2016). These two methods differ mainly in the estimation of the between-study variance, commonly denoted as \(\tau ^{2}\) in the meta-analytic literature. The technical differences between these methods have been summarized elsewhere (e.g., Knapp, Biggerstaff, & Hartung, 2006; Thorlund, Wetterslev, Awad, Thabane, & Gluud, 2011; Veroniki et al., 2016) and will not be discussed here.
When the observed proportions are around 0.5 and the number of studies is sufficiently large, the proportions follow an approximately symmetrical binomial distribution. Under such circumstances, the normal distribution is a good approximation of the binomial distribution, and using the raw proportion as the effect-size metric for analysis is appropriate (Barendregt et al., 2013; Box, Hunter, & Hunter, 2005; Wang & Liu, 2016). Additionally, based on their simulation study, Lipsey and Wilson (2001) suggested that when observed proportions derived from primary studies fall between 0.2 and 0.8, and the focus is solely on the mean proportion across the studies, the raw proportion can be adequately employed as the effect-size metric. The procedure for calculating the effect size, sampling variance, and inverse variance weight for an individual study using the raw proportion is as follows (Lipsey & Wilson, 2001):
The raw proportion is given by: \begin {equation} E{S_p} = p = \frac {k}{n} \end {equation}
with its sampling variance: \begin {equation} Va{r_p} = SE_p^2 = \frac {{p\left ( {1 - p} \right )}}{n} \end {equation}
and the inverse variance weight: \begin {equation} {w_p} = \frac {1}{{Va{r_p}}} = \frac {1}{{SE_p^2}} = \frac {n}{{p\left ( {1 - p} \right )}} \end {equation} where p is the proportion, k is the number of individuals or cases in the category of interest, and n is the sample size. ES, SE, Var, and w stand for effect size, standard error, sampling variance, and inverse variance weight, respectively.
However, when collecting studies for a meta-analysis of proportions, it is observed that proportional data are rarely centered around 0.5 and often exhibit significant skewness (Hunter et al., 2014). As the proportions deviate further from 0.5 and approach closer to the boundaries (particularly when they are below 0.2 or above 0.8), they become less likely to be normally distributed (Lipsey & Wilson, 2001). Additionally, using the raw proportion as the effect-size metric in such situations may underestimate the coverage of the confidence interval around the weighted average proportion and overestimate the level of heterogeneity among the observed proportions (Lipsey & Wilson, 2001). Consequently, relying on the assumption of normality may lead to biased estimation and potentially misleading or invalid inferences (Feng et al., 2014; Ma et al., 2016).
To address the skewness in the distribution of observed proportions, it is common practice to apply transformations to the observed proportions collected for a meta-analysis. This is done to ensure that the transformed proportions conform as closely as possible to a normal distribution, thus enhancing the validity of subsequent statistical analyses (Barendregt et al., 2013). More specifically, all computations and analyses are performed based on the transformed proportions (e.g., the natural logarithm of the proportion) and their inverted variances (i.e., the study weight). The results, such as the summary proportion and its confidence interval, are presented in the original effect-size metric (i.e., proportion) for ease of presentation and interpretation (Borenstein et al., 2009).
In practice, the approximate likelihood approach (Agresti & Coull, 1998) is arguably the predominant framework for modeling proportional data (Hamza et al., 2008; Nyaga, Arbyn, & Aerts, 2014). There are two main ways to transform observed proportions within this framework: the logit or log odds transformation (Sahai & Ageel, 2012) and the Freeman-Tukey double arcsine transformation (Freeman & Tukey, 1950; Miller, 1978). For the logit transformation, the observed proportions are first converted to their natural logarithm of the proportions (i.e., the logit). Following the transformation, the logit transformed proportions are assumed to follow a normal distribution, and all analyses are conducted on the logit scale. Subsequently, the logits are converted back into proportions for reporting and interpretation purposes. The procedure for calculating the logit, its standard error and inverse variance weight for primary studies, as well as the formula for back-transformation, are as follows (Lipsey & Wilson, 2001).
The logit is calculated by: \begin {equation} E{S_l} = {\log _e}\left ( {\frac {p}{{1 - p}}} \right ) = \ln \left ( {\frac {p}{{1 - p}}} \right ) \end {equation}
with its sampling variance: \begin {equation} Va{r_l} = SE_l^2 = \frac {1}{{np}} + \frac {1}{{n(1 - p)}} \label {eq5} \end {equation}
and the inverse variance weight: \begin {equation} {w_l} = \frac {1}{{SE_l^2}} = np\left ( {1 - p} \right ). \end {equation}
To convert the transformed values into proportions, use: \begin {equation} p = \frac {{{e^{logit}}}}{{{e^{logit}} + 1}}. \end {equation}
Being widely employed in meta-analyses of proportions, the logit transformation still has its limitations in certain situations. Two limitations are particularly noteworthy.
First, the issue of variance instability persists even after applying the logit transformation (Barendregt et al., 2013; Hamza et al., 2008). The purpose of data transformation is to bring the skewed data closer to a normal distribution or at least to achieve more consistent variance. While the logit transformation generates a sampling distribution that approximates normality to a greater extent, it fails to stabilize the variance, potentially placing undue weight on studies. According to the equation for sampling variance (Eq. 5), for a fixed value of n, the variance changes with p. For instance, consider a situation with two studies of the same sample size, where an observed proportion close to 0 or 1 yields grossly magnified variance, while an observed proportion around 0.5 yields squeezed variance, leading to variance instability (Barendregt et al., 2013).
Second, when the event of interest is extremely rare (i.e. p = 0) or extremely common (i.e., p = 1), the logits and their sampling variances become undefined. In practice, the common solution is to add an arbitrary constant 0.5 correction to the np and n(1-p) for all studies (Hamza et al., 2008). However, this approach has been shown to introduce additional bias to the results (Lin & Xu, 2020; Ma et al., 2016).
Both of the aforementioned problems can be elegantly solved by employing the variance-stabilizing transformation known as the double arcsine transformation (Freeman & Tukey, 1950), which is accomplished with the following equation3 : \begin {equation} E{S_t} = {\sin ^{ - 1}}\sqrt {\frac {k}{{n + 1}}} + {\sin ^{ - 1}}\sqrt {\frac {{k + 1}}{{n + 1}}} \end {equation}
The sampling variance is computed by: \begin {equation} Va{r_t} = \frac {1}{{n + 0.5}} \end {equation}
The back-transformation is computed by the equation as proposed by Miller (1978): \begin {equation} p = \frac {1}{2}\left [ {1 - sgn\left ( {\cos t} \right )\left [ {1 - {{\left ( {\sin t + \frac {{\sin t - \frac {1}{{\sin t}}}}{{n'}}} \right )}^2}} \right ]^{\frac {1}{2}}} \right ] \label {10} \end {equation} where t denotes the double arcsine transformed value or the confidence interval around it with sgn being the sign operator. In Eq. (10), the total sample size denoted by \(n'\) is calculated as the harmonic mean of individual sample sizes (Miller, 1978). The harmonic mean is defined as: \begin {equation} n' = m{(\mathop \sum \limits _i^m n_i^{ - 1})^{ - 1}} \end {equation} where \(n_{i}\) denotes the sample size of each included study and m denotes the number of included studies. Miller (1978) gives an example in his paper: a meta-analysis of proportions includes four studies with sample sizes being 11, 17, 21, and 6, respectively. The harmonic mean of the four sample sizes will be: \begin {equation} n' = \frac {4}{{\frac {1}{{11}} + \frac {1}{{17}} + \frac {1}{{21}} + \frac {1}{6}}} = 10.9885. \end {equation}
Barendregt et al. (2013) found that Eq. (10) becomes numerically unstable when \(\sin t\) is close to 0 or 1, leading to potentially misleading results. This phenomenon has also been documented by recent publications (Evangelou & Veroniki, 2022; Lin & Xu, 2020; Schwarzer, Chemaitelly, Abu-Raddad, & Rücker, 2019). Instead of the harmonic mean, Barendregt et al. (2013) and Xu et al. (2021) recommend using \(1/\bar {v}\) as the estimate for the total sample size. They propose that the double arcsine back-transformation be implemented as follows: \begin {equation} \bar {p}=\frac {1}{2}\left [ 1-sgn(\cos \bar {t})\left [ 1-\left ( \sin \bar {t}+\frac {\sin \bar {t}-\frac {1}{\sin \bar {t}}}{\frac {1}{\bar {v}}} \right )^{2} \right ]^{\frac {1}{2}} \right ] \label {13} \end {equation} where \(\bar {p}\) is the pooled proportion on the natural scale and \(\bar {v}\) is the pooled variance on the transformed scale. Notice that Eq. (13) uses \(1/\bar {v}\) instead of the harmonic mean.
In summary, raw proportions are adequate when the observed proportions from primary studies fall between 0.2 and 0.8. When observed proportions are less than 0.2 or greater than 0.8, the logit or double arcsine transformation is recommended. It is worth noting that some simulation studies have shown that the double arcsine method slightly outperforms the logit transformation in terms of relative bias, mean squared error, and 95% coverage (Barendregt et al., 2013; Xu et al., 2021). Furthermore, the double arcsine method would be a more appropriate choice when extreme proportions need to be addressed. Last but not least, we recommend Eq. (13) when applying the back-transformation of the double arcsine method.
In a meta-analysis, effect sizes are weighted by the inverse of their sampling variances, giving greater weight to larger studies and allowing their effect sizes to have a greater impact on the overall mean. The weighted average proportion (i.e., the summary proportion) can be computed as follows (Barendregt et al., 2013): \begin {equation} ES_{P}=P=\frac {{\sum \left ( {{w_i}p_{i}} \right )}}{{\sum {w_i}}}=\frac {\sum \frac {p_{i}}{Var_{p_{i}}}}{\sum \frac {1}{Var_{p_{i}}}} \end {equation} with its sampling error: \begin {equation} SE_{p}=\sqrt {\sum w_{i}}=\sqrt {\sum \frac {1}{Var_{p_{i}}}}. \end {equation}
The confidence interval of the weighted average proportion can be expressed as follows: \begin {equation} \begin {array}{l} {P_L} = P - {Z_{\left ( {1 - \alpha } \right )}}\left ( {S{E_P}} \right )\\ {P_U} = P + {Z_{\left ( {1 - \alpha } \right )}}\left ( {S{E_P}} \right ) \end {array} \end {equation} where \(Z_{(1-\alpha )} = 1.96\) when \(\alpha = 0.05.\)
We will now proceed with the first step of our meta-analysis. First, readers need to install and download the necessary R packages. These packages are developed to run within R and contain a collection of functions that are essential for conducting meta-analyses. In this tutorial, we will install two packages: metafor (Viechtbauer, 2010) and meta (Schwarzer et al., 2015). We will primarily rely on metafor and use meta to create forest plots. To install these packages, execute the following command:
install.packages(c("metafor", "meta"))
Once readers have installed a package, it becomes permanently available for use in R on this specific computer. To use the installed packages, one needs to execute the library() function each time you run R. To load metafor and meta into the current R session, type the following R code:
library(metafor) library(meta)
We then need to import data.csv into R and create a data frame named “dat”. This can be achieved by using the read.csv() function and running the following code:
dat <- read.csv("data.csv", header = TRUE, sep = ",")
The code above represents a standard approach to importing .csv files. It instructs R to read a .csv file, interpreting the first row as column names, and recognizing commas as the separators between values.
To estimate the weighted average proportion, we will use the following functions in metafor: escalc(), rma(), and predict(). These functions, in conjunction with a range of arguments to be specified within them, provide instructions to R on how to calculate effect sizes. Note that certain arguments have default values, such as weighted = TRUE, so users don’t need to specify them. The escalc() function estimates an effect size and its standard error for every primary study included in a meta-analysis. Users have the flexibility to decide whether to transform these effect sizes and, if so, which transformation method to employ, by using the measure argument. We will now create a data frame named “ies” (short for individual effect size) to store calculated effect sizes and standard errors using the following generic code:
#Only choose one of the three transformation methods ies <- escalc(xi = cases, ni = total, data = dat, measure = "PR")
Here, the variable “cases” contains the number of events. The variable “total” contains the sample size. We use the argument data to inform R that these variables are contained in the data frame “dat”. By using the argument measure, we can specify which computational method to employ for transforming the raw proportions:
measure = "PR" #No transformation measure = "PLO" #The logit transformation measure = "PFT" #The double arcsine transformation
We will then use the function rma() to pool the derived effect sizes. The function will yield a summary proportion, its standard error, and a 95% confidence interval. Additionally, it will also conduct heterogeneity tests. We can execute the following code to achieve this:
pes <- rma(yi, vi, data = ies, method = "REML")
Although naming an object in R is arbitrary, we strongly recommend that readers assign meaningful names to objects. In this case, if we decide not to perform a transformation, we will name this object “pes”, which stands for pooled effect size. If we decide to perform a transformation with either the logit or the double arcsine, we will name it “pes.logit” or “pes.da”, which stands for logit or double-arcsin transformed pooled effect size, respectively. The object will store all of the outcomes. The method argument dictates which of the following between-study variance estimators will be used (the default method is REML):
method = "DL" #The DL estimator method = "REML" #The REML estimator
If unspecified, rma() estimates the variance component using the REML estimator. Even though rma() stands for random-effects meta-analysis, the function can perform a fixed-effect meta-analysis with the code:
method = "FE"
The object “pes.logit” or “pes.da” now contains the estimated transformed summary proportion. To convert it back to its original, non-transformed scale (i.e., proportion) and yield an estimate for the true summary proportion, we can use the predict() function:
#Inverse of logit transformation pes <- predict(pes.logit, transf = transf.ilogit) #Inverse of double arcsine transformation pes <- predict(pes.da, transf = transf.ipft.hm, targ = list(ni = dat$total))
The argument transf dictates how to convert the transformed proportion back to proportion. As mentioned earlier, we can follow two methods for back-transformation (Eq. 10 or Eq. 13). In either case, we set the transf argument to transf.ipft.hm (the “hm” stands for the harmonic mean). If we opt for the harmonic mean (\(n^{'}\)) in Eq. (10) as the estimate for the total sample size, the sample sizes of primary studies are specified by setting the targ argument to list(ni = dat$total). If we opt to use \(1/\bar {v}\) as the total sample size estimate, then we specify the total sample size as \(1/(pes.da\$se)^2\) within the targ argument and use the following code for back-transformation:
pes <- predict(pes.da, transf = transf.ipft.hm, targ = list(ni=1/(pes.da$se)^2))
Finally, to see the output for the estimated summary proportion and its 95% CI, we can use the print() function:
print(pes)
For the sake of readers’ convenience, we provide readers with generic code for calculating the summary proportion under the random-effects model using three different transformation methods:
# Option 1: no transformation ies <- escalc(xi = cases, ni = total, data = dat, measure = "PR") pes <- rma(yi, vi, data = ies) print(pes) # Option 2: the logit transformation ies.logit <- escalc(xi = cases, ni = total, data = dat, measure = "PLO") pes.logit <- rma(yi, vi, data = ies.logit) pes <- predict(pes.logit, transf = transf.ilogit) print(pes) # Option 3: the double arcsine transformation # targ can also be set to list(ni = 1/(pes.da$se)^2) ies.da <- escalc(xi = cases, ni = total, data = dat, measure = "PFT", add = 0) pes.da <- rma(yi, vi, data = ies.da) pes <- predict(pes.da, transf = transf.ipft.hm, targ = list(ni = dat$total)) print(pes)
Note the use of add = 0 in Option 3. When a study contains proportions equal to 0, the escalc() function will automatically add 0.5 to the observed data (i.e., the “cases” variable). Since the double arcsine transformation does not require any adjustments to be made to the data in such a situation, we can explicitly switch add = 0.5 to add = 0 to prevent the default adjustment.
Returning to the running example, we chose Option 2 (i.e., the logit transformation) to calculate the summary proportion because all of the observed proportions in the dataset are far below 0.2:
ies.logit <- escalc(xi = cases, ni = total, measure = "PLO", data = dat) pes.logit <- rma(yi, vi, data = ies.logit, method = "DL", level = 95) pes <- predict(pes.logit, transf = transf.ilogit) print(pes, digits = 6)
The argument digits specifies the number of decimal places to which the printed results should be rounded, with the default value being 4. The argument level specifies the confidence interval, with the default value set to 95%.4
The estimated summary proportion and its 95% CI are shown in Figure 1. Interpreting these summary statistics, we find that the summary proportion is estimated to be 0.000424 and its 95% CI is between 0.000316 and 0.000569.
pred ci.lb ci.ub cr.lb cr.ub 0.000424 0.000316 0.000569 0.000133 0.001347
Meta-analysis aims to synthesize studies and estimate a more precise summary effect. An important decision that all meta-analysts face is whether it is appropriate to combine a set of identified studies in a meta-analysis, given the inevitable differences in their characteristics to varying degrees. Combining studies with substantially different effect estimates can result in an inaccurate summary effect and an unwarranted conclusion. For example, in a meta-analysis of proportions regarding re-offending rates among juvenile offenders in a city, the summary proportion may fall within a medium range (around 0.5). However, considerable variation exists among these proportions, with some studies conducted in certain boroughs reporting small proportions (e.g., under 0.1), while others report very large proportions (e.g., above 0.9). Simply reporting a moderately large mean proportion would be misleading, as it fails to acknowledge the significant variation or inconsistency in effect sizes across the studies. This variation is known as heterogeneity (Del Re, 2015). We will introduce three quantifying statistics for heterogeneity in this section: \(\tau ^{2}\), \(Q\), and \(I^{2}\).
Heterogeneity can be quantified by dividing it into two distinct components: the between-study variance, which arises from the true variation among a body of studies, and the within-study variance, resulting from the sampling error. The true variation can be attributed to clinical and/or methodological diversity, in other words, the systematic differences between studies beyond what would be expected by chance, such as experimental designs, measurements, sample characteristics, interventions, study settings, and combinations thereof (Lijmer, Bossuyt, & Heisterkamp, 2002; Thompson & Higgins, 2002). In this tutorial, we focus on the true variation in effect sizes, namely the between-study heterogeneity.
We characterize between-study heterogeneity by the variance of the true effect size underlying the data, \(\tau ^{2}\), a statistic called tau-squared. Under the assumption of normality, 95% of the true effects are expected to fall within \(\pm \) \(1.96\times \tau \) of the point estimate of the summary effect size (Borenstein, Hedges, Higgins, & Rothstein, 2010). \(\tau ^{2}\) reflects the total amount of systematic differences in effects across studies. The total variance of a study consists of the between- and within-study heterogeneity and is used to assign weights under the random-effects model (i.e., the inverse of the total variance).
In classic inverse variance meta-analysis, \(\tau ^{2}\) can be estimated by numerous methods, as mentioned in Section 4 (e.g., REML, DL). Review and simulation studies have shown that both methods perform satisfactorily well across various situations; the differences between their results are negligible and rarely significant enough to impact the qualitative conclusions (e.g., Hamza et al., 2008; Thorlund et al., 2011; Veroniki et al., 2016). Nevertheless, it is advisable to obtain the 95% confidence interval around the point estimate of \(\tau ^{2}\), especially when the number of included studies is small (less than 5) (Veroniki et al., 2016).
In practice, the DerSimonian and Laird estimator is arguably the most commonly used statistical method for meta-analyses of proportions and has become the conventional and default method for assessing the amount of between-study heterogeneity in many software packages, such as CMA (Cornell et al., 2014; Schwarzer et al., 2015). All estimations in this tutorial are based on the DL method.
Using formal tests, the presence of between-study heterogeneity is generally examined using a \(\chi ^{2}\) test with a statistic Q (Cochran, 1954) under the null hypothesis that all studies share the same true effect (Hedges & Olkin, 1985). In other words, the Q-test and its p-value serve as a test of significance to address the null hypothesis: \(H_{0}: \tau ^{2}=0\). If the value of the Q-statistic is above the critical \(\chi ^{2}\) value, we will reject the null hypothesis and conclude that the effect sizes are heterogeneous. Under such circumstances, you may consider taking the random-effects model route. If Q does not exceed this value, then we fail to reject the null hypothesis.
It is important to exercise caution when interpreting a non-significant p-value and drawing the conclusion of homogeneous true effects. The statistical power of the Q-test heavily relies on the number of studies included in a meta-analysis, and as a result, it may fail to detect heterogeneity due to limited power when the number of included studies is small (less than 10) or when the included studies are of small size (Huedo-Medina, Snchez-Meca, Marn-Martnez, & Botella, 2006). Therefore, a non-significant result should not be taken as showing empirical evidence for homogeneity (Hardy & Thompson, 1998). This issue warrants serious attention, considering that a significant proportion of meta-analyses in Cochrane reviews involve only five or fewer studies (Davey, Turner, Clarke, & Higgins, 2011).
Furthermore, it is important to note that the Q-test, in addition to its aforementioned limitation, only assesses the viability of the null hypothesis and does not provide a quantification of the magnitude of the true heterogeneity in effect sizes (Card, 2015).
Higgins, Thompson, Deeks, and Altman (2003) proposed a statistic for measuring heterogeneity, denoted as \(I^{2}\), that remains unaffected by the number of included studies. In essence, it reflects the ratio of the observed heterogeneity, representing the true between-study variance, to the total observed heterogeneity (i.e., the sum of between- and within-study variance). As a result, it facilitates the comparison of heterogeneity estimates across meta-analyses, regardless of the original scale used in the meta-analyses themselves.
\(I^{2}\) can take values from 0% to 100%. A value of 0% indicates that all heterogeneity is caused by sampling error alone, requiring no further explanation. Conversely, when \(I^{2}\) equals 100%, the entire heterogeneity can be attributed exclusively to genuine differences between studies, thus justifying the application of subgroup analyses or meta-regressions to identify potential moderating factors. The thresholds of 25%, 50%, and 75% are commonly used to indicate low, medium, and high heterogeneity, respectively (Higgins et al., 2003) . Note that these thresholds only serve as tentative benchmarks for \(I^{2}\). The 95% CI around the \(I^{2}\) statistic should also be calculated (Cuijpers, 2016; Ioannidis, Patsopoulos, & Evangelou, 2007).
Relying solely on the value of \(I^{2}\) can be misleading because a 0% \(I^{2}\), accompanied by a 95% CI ranging from 0% to 80%, does not necessarily indicate homogeneity in a small meta-analysis study. Rather, the degree of heterogeneity remains uncertain in such cases.
An important caveat
Together, the Q-statistic, \(\tau ^{2}\), and \(I^{2}\) can inform us if the effects are homogeneous, or consistent. When the effect sizes are reasonably consistent, it is appropriate to combine them and present a summary effect size in reports. In cases where moderate and substantial heterogeneity is present, the summary effect size becomes less informative or even of no value. In such cases, we strongly suggest that researchers conduct moderator analyses to thoroughly explore the possible sources of heterogeneity in observed effect sizes rather than relying solely on the mechanistic calculation of a single mean effect estimate (Egger, Schneider, & Smith, 1998). We will discuss moderator analysis in more detail later.
However, it is important to note that the methods used to estimate the amount of heterogeneity and conduct significance tests for heterogeneity are not always reliable, potentially leading to misleading interpretations of the variability of the true effect size. Relying solely on the Q-test is ill-advised due to its inadequate power to detect low heterogeneity (Chung, Rabe-Hesketh, & Choi, 2013; Rücker, Schwarzer, Carpenter, & Schumacher, 2008). Furthermore, the rules of thumb benchmarks for \(I^{2}\) only hold true when the within-study error is relatively constant (Borenstein, Higgins, Hedges, & Rothstein, 2017). Underestimating between-study heterogeneity or failing to detect any heterogeneity due to inadequate statistical power can result in authors fitting the wrong model (i.e., the fixed-effect model), leading to inaccurate inferences about the overall effect (Higgins & Thompson, 2002; Thompson, 1994; Thompson & Sharp, 1999).
Heterogeneity tests provide only a single piece of evidence when deciding between the fixed- and random-effects models. The choice of model should consider a range of factors, including the sampling frame, the desired type of inference, expectations about the distribution of the true effect, and the statistical significance of the heterogeneity tests, among others. Borenstein (2019) suggested that when studies in a meta-analysis are collected from the literature, a random-effects model is almost always preferable. This is because the true effect size is likely to vary across studies unless they were conducted by the same lab, following identical protocols, and using consistent materials on the same population. Furthermore, if we intend to make an inference to comparable populations, as is common in social sciences, the random-effects model becomes the only appropriate choice.
To view the results of the heterogeneity test (Cochran’s Q) and the estimates of between-study variance (\(\tau ^{2}\)) and \(I^{2}\), we still use the print() function:
# Note, if you selected other transformation methods, # then type pes.logit or pes.da in print() print(pes)
The confint() function computes and displays the confidence intervals for \(\tau ^{2}\) and \(I^{2}\):
# If you selected other transformation methods, # then type pes.logit or pes.da in confint() confint(pes)
To display the output of heterogeneity-related results for the running example, we can type:
print(pes.logit, digits = 4) confint(pes.logit, digits = 4)
The output appears in Figure 2. It reveals that \(\tau ^{2}\) is 0.3256 (95% CI = 0.3296, 1.4997), \(I^{2}\) is 97.24% (95% CI = 97.28, 99.39), and the Q-statistic is 580.5387 (p <.001), all of which suggests high heterogeneity in the observed proportions.5
Random-Effects Model (k = 17; tau^2 estimator: DL) tau^2 (estimated amount of total heterogeneity): 0.3256 (SE = 0.2033) tau (square root of estimated tau^2 value): 0.5707 I^2 (total heterogeneity / total variability): 97.24% H^2 (total variability / sampling variability): 36.28 Test for Heterogeneity: Q(df = 16) = 580.5387, p-val < .0001 Model Results: estimate se zval pval ci.lb ci.ub -7.7650 0.1502 -51.7147 <.0001 -8.0593 -7.4707 *** --- Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 . 0.1 1 estimate ci.lb ci.ub tau^2 0.3256 0.3296 1.4997 tau 0.5707 0.5741 1.2246 I^2(%) 97.2439 97.2758 99.3884 H^2 36.2837 36.7079 163.4972
This section is dedicated to visualization tools and a few formal diagnostic tests pivotal for heterogeneity analyses. We introduce two essential tools for readers: the forest plot and the Baujat plot. The forest plot allows for a visual assessment of the homogeneity across studies, while the Baujat plot can pinpoint studies that exert a significant impact on the overall effect, heterogeneity, or both. It’s crucial to introduce the forest plot at this point. It lays the foundation for our in-depth demonstration of its application in subgroup analyses, which we will discuss in Section 7.
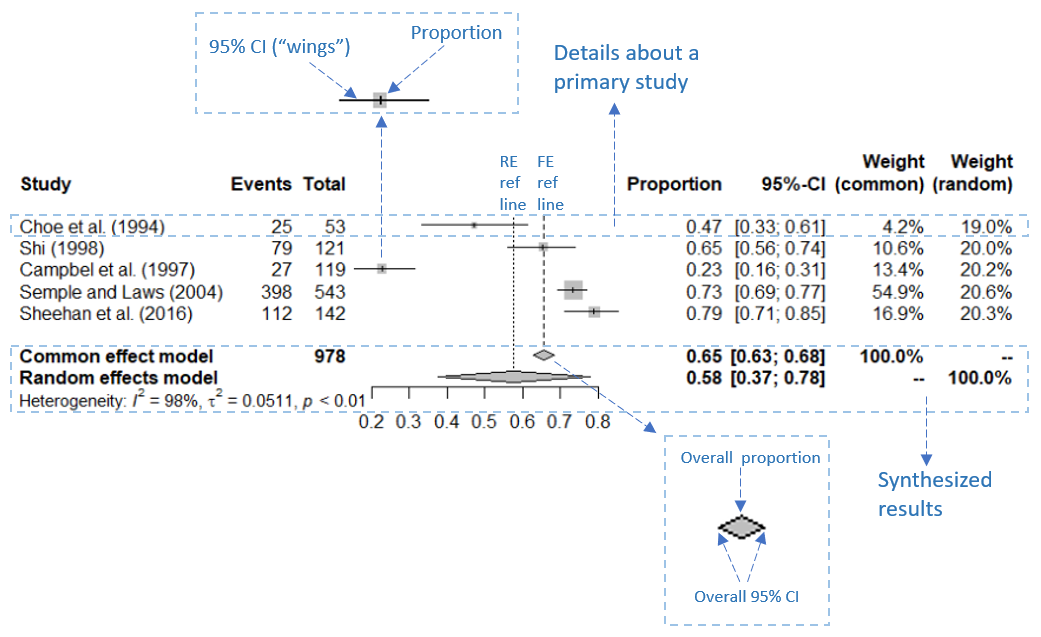
A forest plot (as shown in Figure 3) is a graphical representation that effectively displays the point estimates of study effects along with their corresponding confidence intervals (Lewis & Clarke, 2001). It is composed of a vertical reference line, an x-axis, and graphical representations of effect size estimates and their 95% CIs. The x-axis of the forest plot represents the scale of the outcome measure (in our case, the proportion) and can range from 0 to 1.
Typically, the vertical reference line is positioned at the point estimate of the pooled proportion. At the bottom of the reference line lies a colored diamond shape with its length representing the 95% confidence interval of the pooled proportion. Each study effect plotted in a forest plot consists of two components: a colored square symbolizing the point estimate of the study effect size and a horizontal line through the square representing the confidence interval around the point estimate. I refer to the horizontal lines as the squares’ ”wings”, if you will.
The size of a square corresponds to the study’s weight; a larger square signifies a larger sample size and, therefore, a greater weight. An effect size with a greater weight carries more influence on the summary effect size and is therefore depicted by a larger square with a shorter horizontal line (Anzures-Cabrera & Higgins, 2010).
In a forest plot, study effects are determined as homogeneous if all the horizontal lines of the squares overlap (Petrie, Bulman, & Osborn, 2003; Ried, 2006). The forest plot also allows us to identify potential outliers. This can be achieved by examining studies whose 95% confidence intervals do not overlap with the confidence interval of the summary effect size (Harrer, Cuijpers, A, & Ebert, 2021). Furthermore, it is worth noting that if large studies are identified as outliers, it may suggest that the overall heterogeneity is high.

In this section, we will begin by explaining how to create a basic forest plot using the meta package. We will also show readers how to create a more sophisticated, publication-ready forest plot.
We can create a simple forest plot using the following generic code (assuming that we have loaded the meta package):
pes.summary <- metaprop(cases, total, authoryear, data = dat, sm = "PRAW") forest(pes.summary)
Using the metaprop() function, we conduct a meta-analysis of proportions and save the results in an object named “pes.summary”. We then feed these results into the forest() function to automatically generate a forest plot. The sm argument in the metaprop() function dictates which transformation method will be used to convert the original proportions:
PRAW # no transformation PLO # the logit transformation PFT # the double arcsine transformation
Forest plots created by the generic code are bare-boned and often fail to meet publishing standards. The following code can produce publication-quality forest plots for the running example:
pes.summary <- metaprop(cases, total, authoryear, data = dat, sm = "PLO", method.tau = "DL", method.ci = "NAsm") forest(pes.summary, common = FALSE, print.tau2 = TRUE, print.Q = TRUE, print.pval.Q = TRUE, print.I2 = TRUE, rightcols = FALSE, pooled.totals = FALSE, weight.study = "random", leftcols = c("studlab", "event", "n", "effect", "ci"), leftlabs = c("Study", "Cases", "Total", "Prevalence", "95% C.I."), xlab = "Prevalence of CC (%)", smlab = "", xlim = c(0,4), pscale = 1000, squaresize = 0.5, fs.hetstat = 10, digits = 2, col.square = "navy", col.square.lines = "navy", col.diamond = "maroon", col.diamond.lines = "maroon")
The generated forest plot is shown in Figure 4.
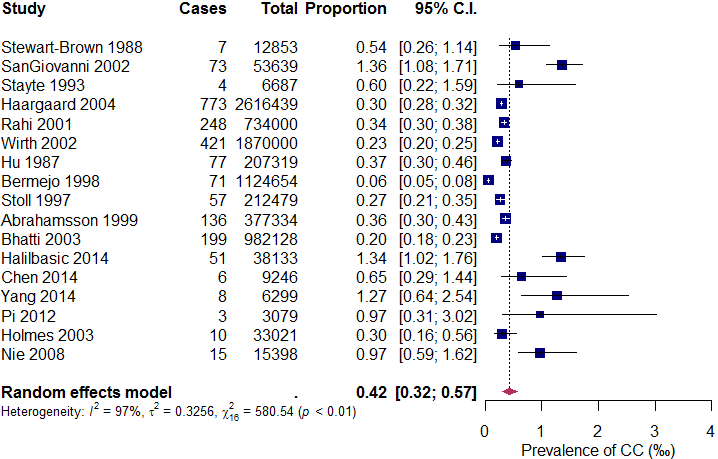
The arguments in forest() provided above are mostly self-explanatory. They determine which components of the forest plot are displayed, as well as their colors, sizes, and positions on the graph. The pscale argument is particularly noteworthy. Setting “pscale = 1000” means that the prevalence is expressed as events per 1,000 observations. Consequently, the combined proportion under the random-effects model is displayed as 0.42‰ in the forest plot6 . It should be mentioned that due to space constraints, we have only listed the most essential arguments in the forest() function. Readers are encouraged to refer to the documentation that comes with the meta package (type ?meta::forest() in R) to explore additional useful arguments for customizing their own forest plots.
We can sort the individual studies by precision to help us visually inspect the data. This can be achieved by sorting the included studies using SE or the inverse of SE:
precision <- sqrt(ies.logit$vi)
We then add the sortvar argument in the forest() function:
sortvar = precision
The new forest plot is shown in Figure 5. This forest plot clearly shows that the prevalence of CC is higher in smaller studies (those with longer “wings”). In meta-analyses of comparative studies, a forest plot without indications of publication bias will exhibit an even spread of studies with varying precision on both sides of the mean effect size. However, in a meta-analysis of observational data, an uneven spread of studies may actually reflect a genuine pattern in effect sizes rather than publication bias, especially when small studies fall to the right side of the mean. It is also possible that some small studies are not published due to valid reasons, such as the use of inadequate research methods. Thus, this uneven distribution of effects warrants further investigation as it may provide new insights into the topic of interest.
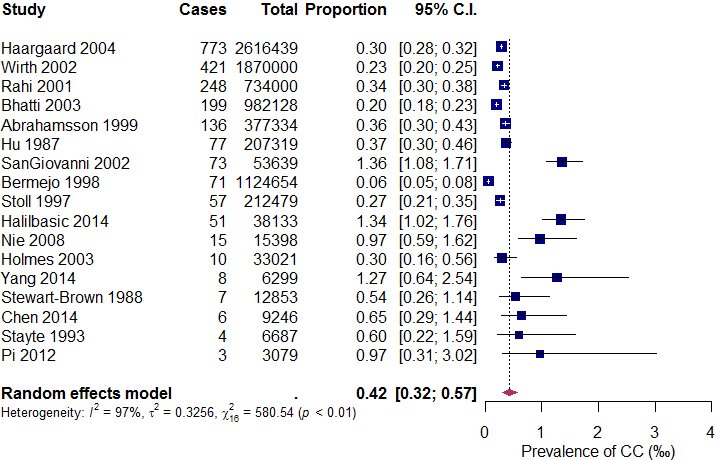
A visual inspection of the forest plot identifies several potential outlying studies, including Wirth (2002), Bhatti (2003), SanGiovanni (2002), Bermejo (1998), Halilbasic (2014), Nie (2008), and Yang (2014). Their 95% CIs do not overlap with that of the summary proportion. In the next step, we will cross-validate these potential outliers using the Baujat plot.
When dealing with high between-study heterogeneity in a meta-analysis, one approach is to identify and exclude outliers, and then reassess the robustness of the summary effect size. In this section, we will introduce some diagnostic tools that can identify outlying and influential studies.
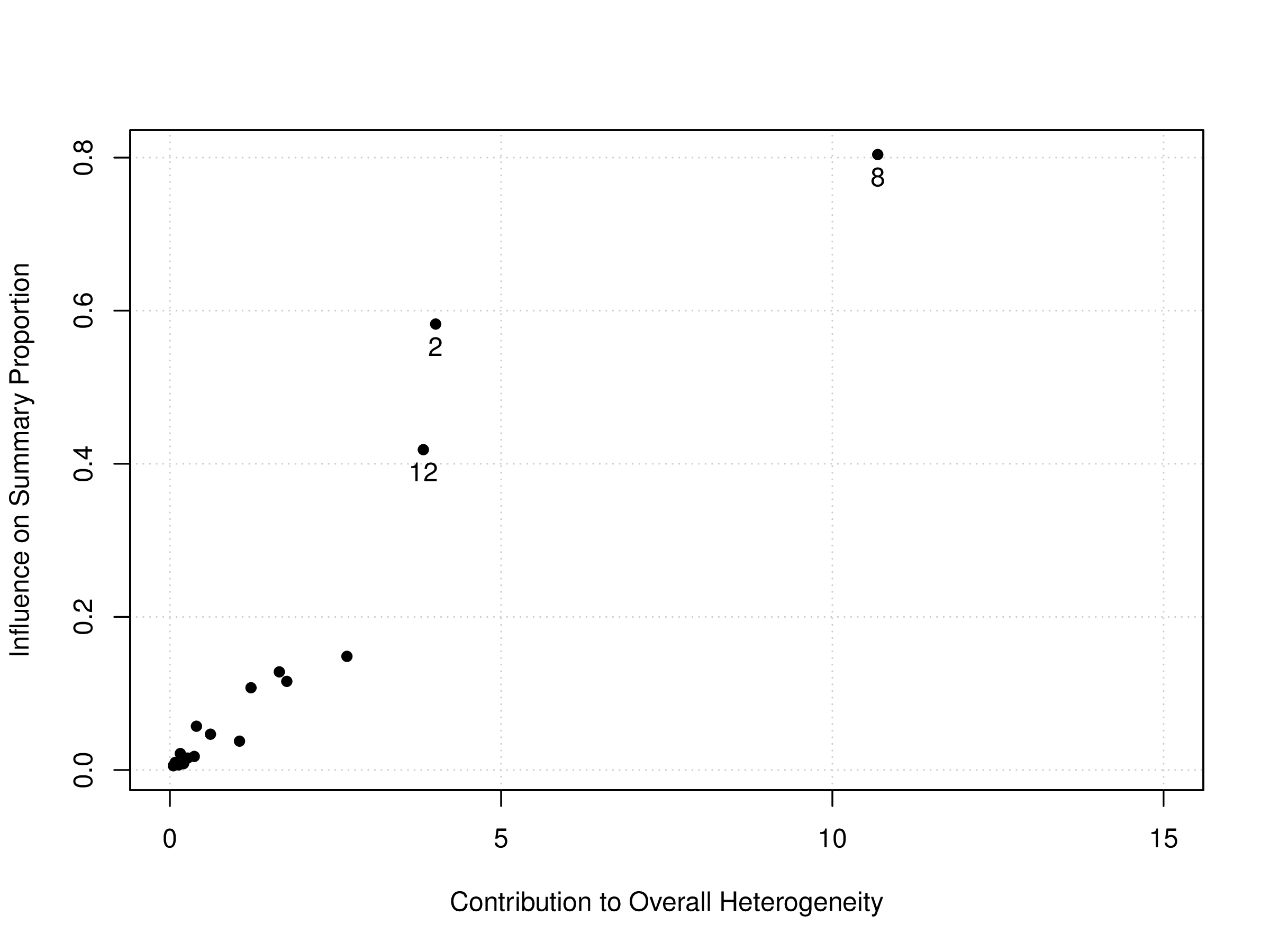
A basic Baujat plot is depicted in Figure 6. The horizontal axis of the Baujat plot quantifies each study’s contribution to the overall heterogeneity or the Cochran Q-test, while the vertical axis measures the impact of each study on the summary effect size. We’ve divided the Baujat plot into four quadrants with light blue dotted lines for illustration purposes. Studies situated far to the right on the horizontal axis (in Quadrants 2 and 3) are significant contributors to heterogeneity. Those positioned far up on the vertical axis (in Quadrants 1 and 2) substantially influence the overall meta-analysis result. A study’s influence is deemed substantial if its removal would lead to a drastically different overall effect.
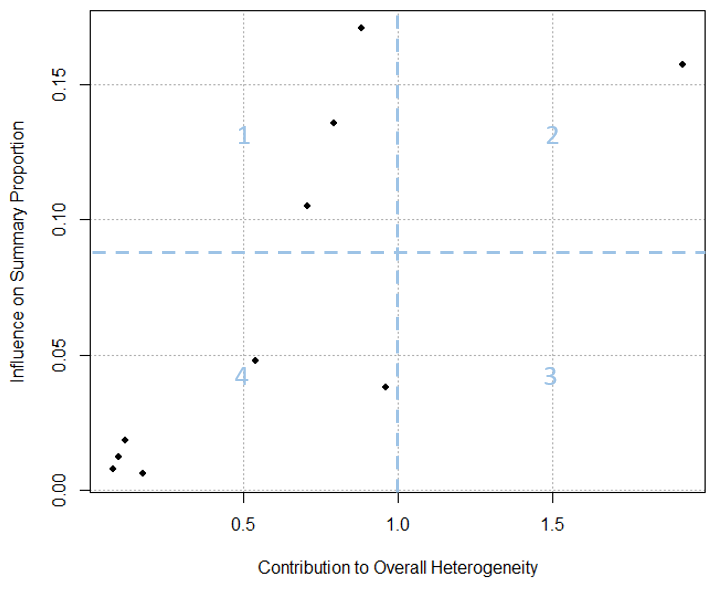
It can sometimes be challenging to differentiate between the concepts of an “outlier” and an “influential effect size” in the context of meta-analysis. While an outlying effect size can often be influential, it isn’t always so. Conversely, an effect size that is influential doesn’t necessarily have to be an outlier (Harrer et al., 2021). The Baujat plot helps distinguish between outliers that are influential and those that are not:
It is crucial to conduct several formal diagnostic tests to determine if the outlying effect sizes identified in the forest plot and Baujat plot are truly outliers. If deemed outliers, further investigation is required to determine their actual influence on the overall effect size. Viechtbauer and Cheung (2010) have proposed a set of case deletion diagnostics derived from linear regression analyses to identify influential studies, such as difference in fits values (DFFITS), Cook’s distances, leave-one-out estimates for the amount of heterogeneity (i.e., \(\tau ^{2}\)) as well as the test statistic for heterogeneity (i.e., Q-statistic). In leave-one-out analyses, each study is removed sequentially, and the summary proportion is re-estimated based on the remaining n-1 studies. This approach allows for the assessment of each study’s influence on the summary proportion.
Outlying effect sizes can also be identified by screening for externally studentized residuals exceeding an absolute value of 2 or 3 (Tabachnick, Fidell, & Osterlind, 2013; Viechtbauer & Cheung, 2010).
As a final note, instead of simply removing outlying effect sizes, meta-analysts should investigate these outliers and influential cases to understand their occurrence. They sometimes reveal valuable study characteristics that may serve as potential moderating variables.
In this section, we will use the Baujat plot and diagnostic tests introduced above to detect outliers and influential studies. The generic code for Baujat plot is provided below:
baujat(pes) # or pes.logit, pes.da
For the running example, use the following code to create a customized Baujat plot:
# Create a Baujat plot bjplot <- baujat(pes.logit, symbol=19, xlim=c(0,15), xlab="Contribution to Overall Heterogeneity", ylab="Influence on Summary Proportion") # Label those studies located in the upper quadrants bjplot <- bjplot[bjplot$x >= 10 | bjplot$y >= 0.4,] text(bjplot$x, bjplot$y, bjplot$slab, pos=1)
The generated plot can be seen in Figure 7. In this customized Baujat plot, we have labeled only a few of the more “extreme” studies, specifically: SanGiovanni (2002) (Study 2), Bermejo (1998) (Study 8), and Halilbasic (2014) (Study12). We observe that both Study 2 and Study 12 may be considered influential, though they might not contribute heavily to the overall heterogeneity. In contrast, Study 8 stands out as an influential outlier, as it has a large impact on both the pooled proportion and heterogeneity.
Next, we screen for large externally studentized residuals (ESR). The code below calculates the ESR for each study in the current dataset, then sorts them in descending order based on the absolute values of the z-scores tied to their respective ESRs:
# Calculate ESR stud.res <- rstudent(pes.logit) # or pes, pes.da # Sort ESR by z-values in descending order abs.z <- abs(stud.res$z) stud.res[order(-abs.z)]
The test outcome appears in Figure 8. The key here is to locate studies with z-values that exceed an absolute value of 2 or 3. Since we only have 17 studies in the running example, we will set the threshold at 2. Therefore, the second, eighth, and twelfth studies are chosen. They match the studies we previously identified through the Baujat plot.
resid se z 8 -2.0265 0.5183 -3.9101 2 1.2701 0.5183 2.4505 12 1.2415 0.5541 2.2407 14 1.1563 0.6831 1.6928 17 0.8840 0.6382 1.3853 11 -0.7967 0.6198 -1.2854 6 -0.6895 0.6576 -1.0485 15 0.8618 0.8254 1.0441 9 -0.4925 0.6177 -0.7973 13 0.4459 0.7182 0.6209 4 -0.4063 0.7250 -0.5604 16 -0.3563 0.6727 -0.5297 3 0.3579 0.7743 0.4622 5 -0.2520 0.6444 -0.3911 1 0.2627 0.7021 0.3741 10 -0.1790 0.6231 -0.2872 7 -0.1447 0.6162 -0.2348
The following code performs a set of leave-one-out diagnostic tests:
# Option 1: no transformation # L1O stands for leave-one-out L1O <- leave1out(pes); print(L1O) # Option 2: the logit transformation L1O <- leave1out(pes.logit, transf = transf.ilogit) print(L1O) # Option 3: the double arcsine transformation # targ can also be set to list(ni = 1/(pes.da$se)^2) L1O <- leave1out(pes.da, transf = transf.ipft.hm, targ = list(ni = dat$total)) print(L1O)
Using the current data set, we execute the following code:
L1O <- leave1out(pes.logit, transf = transf.ilogit) print(L1O, digits = 6)
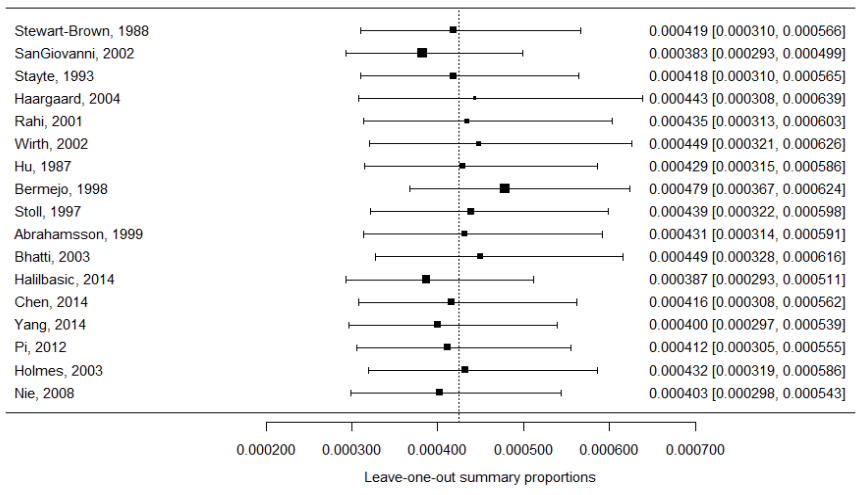
The output is shown in Figure 9. The numbers in the first column are the leave-one-out estimates for the summary proportion, which are derived by excluding one study at a time from the included studies. For instance, the first estimate in this column (i.e., 0.000419) is the summary proportion estimate when the first study in the included studies is removed.
estimate zval pval ci.lb ci.ub Q Qp tau2 I2 H2 1 0.000419 -50.492057 0.000000 0.000310 0.000566 577.938615 0.000000 0.326294 97.404569 38.529241 2 0.000383 -58.124097 0.000000 0.000293 0.000499 405.001830 0.000000 0.236593 96.296313 27.000122 3 0.000418 -50.760057 0.000000 0.000310 0.000565 578.562279 0.000000 0.325980 97.407366 38.570819 4 0.000443 -41.417189 0.000000 0.000308 0.000639 580.526132 0.000000 0.489631 97.416137 38.701742 5 0.000435 -46.319695 0.000000 0.000313 0.000603 575.730710 0.000000 0.383340 97.394615 38.382047 6 0.000449 -45.217145 0.000000 0.000321 0.000626 540.974670 0.000000 0.400959 97.227227 36.064978 7 0.000429 -48.854385 0.000000 0.000315 0.000586 576.473491 0.000000 0.341576 97.397972 38.431566 8 0.000479 -56.505027 0.000000 0.000367 0.000624 404.914535 0.000000 0.236229 96.295515 26.994302 9 0.000439 -48.899481 0.000000 0.000322 0.000598 579.956198 0.000000 0.338978 97.413598 38.663747 10 0.000431 -47.992385 0.000000 0.000314 0.000591 574.985048 0.000000 0.354815 97.391237 38.332337 11 0.000449 -47.824077 0.000000 0.000328 0.000616 548.816035 0.000000 0.353117 97.266844 36.587736 12 0.000387 -55.147300 0.000000 0.000293 0.000511 461.941616 0.000000 0.267048 96.752836 30.796108 13 0.000416 -50.664580 0.000000 0.000308 0.000562 576.843109 0.000000 0.325434 97.399640 38.456207 14 0.000400 -51.312960 0.000000 0.000297 0.000539 563.535902 0.000000 0.318164 97.338235 37.569060 15 0.000412 -51.101371 0.000000 0.000305 0.000555 576.283345 0.000000 0.324438 97.397114 38.418890 16 0.000432 -50.008941 0.000000 0.000319 0.000586 580.534075 0.000000 0.328479 97.416172 38.702272 17 0.000403 -51.136341 0.000000 0.000298 0.000543 559.149838 0.000000 0.317149 97.317356 37.276656
A leave-one-out forest plot can visualize the change in the summary effect size. The generic code is given below:
# Option 1: no transformation l1o <- leave1out(pes) yi <- l1o$estimate; vi <- l1o$se^2 forest(yi, vi, slab = paste(dat$author, dat$year, sep = ","), refline = pes$b, xlab = "Leave-one-out summary proportions") # Option 2: the logit transformation l1o <- leave1out(pes.logit) yi <- l1o$estimate; vi <- l1o$se^2 forest(yi, vi, transf = transf.ilogit, slab = paste(dat$author, dat$year, sep = ","), refline = pes$pred, xlab = "Leave-one-out summary proportions") # Option 3: the double arcsine transformation # targ can also be set to list(ni = 1/(pes.da$se)^2) l1o <- leave1out(pes.da) yi <- l1o$estimate; vi <- l1o$se^2 forest(yi, vi, transf = transf.ipft.hm, targ = list(ni = dat$total), slab = paste(dat$author, dat$year, sep = ","), refline = pes$pred, xlab = "Leave-one-out summary proportions")
To generate a customized leave-one-out forest plot for the current data set, use the following code:
l1o=leave1out(pes.logit) yi=l1o$estimate; vi=l1o$se^2 forest(yi, vi, transf=transf.ilogit, slab=paste(dat$author,dat$year,sep=", "), xlab="Leave-one-out summary proportions", refline=pes$pred, digits=6) abline(h=0.1)
The generated forest plot is shown in Figure 10. Each black square represents a leave-one-out summary proportion. The reference line indicates where the original summary proportion lies. The further a box deviates from the reference line, the more pronounced the impact of the corresponding excluded study will be on the original summary proportion. For instance, if we exclude the study by SanGiovanni et al. (2002), the new summary proportion becomes 0.00038. If we exclude Stayte et al. (1993), the new summary proportion becomes 0.000418. Apparently, excluding the former study has a larger impact on the original summary proportion than the latter study.
With these potential influential studies in mind, we now conduct a few more leave-one-out diagnostics with the influence() function in metafor to verify our guesses:
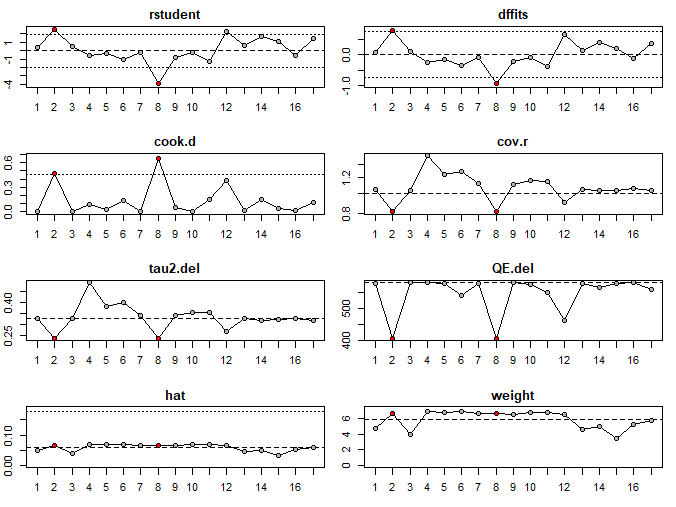
inf <- influence(pes.logit) print(inf, digits=3) plot(inf)
In Figure 11, studies marked with an asterisk are potential influential studies:
rstudent dffits cook.d cov.r tau2.del QE.del hat weight dfbs inf 1 0.374 0.083 0.007 1.052 0.326 577.939 0.048 4.811 0.083 2 2.451 0.801 0.474 0.813 0.237 405.002 0.066 6.643 0.791 * 3 0.462 0.093 0.009 1.042 0.326 578.562 0.039 3.915 0.093 4 -0.560 -0.242 0.088 1.541 0.490 580.526 0.069 6.896 -0.247 5 -0.391 -0.151 0.027 1.239 0.383 575.731 0.068 6.839 -0.152 6 -1.049 -0.336 0.139 1.289 0.401 540.975 0.069 6.873 -0.339 7 -0.235 -0.077 0.006 1.117 0.342 576.473 0.067 6.658 -0.077 8 -3.910 -0.941 0.653 0.812 0.236 404.915 0.066 6.636 -0.929 * 9 -0.797 -0.223 0.052 1.109 0.339 579.956 0.066 6.569 -0.224 10 -0.287 -0.103 0.011 1.156 0.355 574.985 0.068 6.770 -0.103 11 -1.285 -0.369 0.148 1.152 0.353 548.816 0.068 6.818 -0.371 12 2.241 0.674 0.377 0.900 0.267 461.942 0.065 6.530 0.669 13 0.621 0.136 0.019 1.047 0.325 576.843 0.046 4.578 0.136 14 1.693 0.395 0.153 1.031 0.318 563.536 0.050 5.001 0.395 15 1.044 0.197 0.039 1.032 0.324 576.283 0.034 3.420 0.198 16 -0.530 -0.128 0.017 1.064 0.328 580.534 0.053 5.296 -0.128 17 1.385 0.350 0.120 1.036 0.317 559.150 0.057 5.746 0.350
The diagnostics plots in Figure 12 show that the second and eighth studies are colored in red, indicating that they fulfill the criteria as influential studies.
Based on the Baujat plot and the outcomes of the diagnostic tests, we determine that all three studies (Study 2, 8, and 12) can be considered outliers, but only Study 2 and 8 are deemed influential.
Once all possible outliers are identified, we can remove them with the following generic code:
# Depending on the transformation method, # measure = "PLO" or measure = "PFT" # Remember to add "add = 0" when using the # double arcsine transformation ies.noutlier <- escalc(xi = cases, ni = total, measure = "PR", data = dat[-c(study1, study2,),])
If we were to exclude Study 2 and Study 8 in the current data set, we would execute the following code:
# Remove the two studies and calculate individual # effect sizes ies.logit.noutlier <- escalc(xi = cases, ni = total, measure = "PLO", data = dat[-c(2, 8),]) # Conduct meta-analysis with no outliers pes.logit.noutlier <- rma(yi, vi, data = ies.logit.noutlier, method = "DL") pes.noutlier <- predict(pes.logit.noutlier, transf = transf.ilogit) print(pes.noutlier, digits = 5)
We’ve determined that our data shows significant heterogeneity. Furthermore, we identified several outlying studies that notably impact both the overall effect and the variability of the observed effect sizes. When substantial heterogeneity remains even after excluding these outliers, one commonly employed strategy to unearth additional sources of heterogeneity is through moderator analyses. In fact, a thorough moderator analysis can often yield deeper insights than a mere estimate of summary effect size. This analysis helps identify and quantify the extent to which certain study-level characteristics contribute to the observed heterogeneity.
Subgroup analysis and meta-regression are two major forms of moderator analysis. Subgroup analysis can be seen as a special case of meta-regression, which examines the impact of a single categorical variable (Thompson & Higgins, 2002). In fact, meta-regression can accommodate both categorical and continuous moderators of desired numbers. For instance, a meta-regression can include a series of continuous variables or a mix of both continuous and categorical variables. In this tutorial, our focus will be on subgroup analysis and meta-regression with a continuous moderator.
When we want to explain heterogeneity with a categorical moderator in a meta-analysis, subgroup analysis is the method of choice. This approach mirrors the logic of ANOVA in primary research (Littell, Corcoran, & Pillai, 2008). In a subgroup analysis, studies are partitioned into two or more subgroups according to the categories within the moderator. This moderator represents a specific study characteristic that can potentially explain a portion of the variability observed between studies (Hamza et al., 2008). If a subgroup has a unique characteristic absent in other subgroups (e.g., exposure to a new treatment vs. an old treatment), and the effect sizes between the subgroups show significant differences, it suggests that the variation in effect sizes (i.e., the true heterogeneity) can be attributed to this unique characteristic. In essence, the purpose of subgroup analysis is to ascertain if the chosen moderator accounts for a significant portion of the true heterogeneity.
To evaluate the influence of a proposed moderator, we apply a weighted least squares (WLS) regression. In this approach, effect sizes (e.g., those transformed using logit or double arcsine methods) are regressed against the moderator (Harrer et al., 2021): \begin {equation} ES_i ={\beta _0} + {\beta _1}C +\delta _i + e_i \label {17} \end {equation} where \(ES_i\) is the observed effect size for the primary study i, C is the dummy variable representing the moderator (or predictor), \(\beta _{1}\) is the regression coefficient (or slope), and \(\beta _{0}\) is the model intercept. \(\delta _i\) and \(e_i\) are error terms. Specifically, \(\delta _i\) is the between-study error for the primary study i, with its variance being the between-study variance, \(\tau ^2\); \(e_i\) is the sampling error for the primary study i, with its variance being the within-study variance. The goal of the meta-regression model is to estimate the parameters, \(\beta _0\) and \(\beta _1\).
The categorical moderator is introduced in the analysis through dummy coding (e.g., the “studesg” variable in our data set). Let’s say we have two categories within this predictor: Subgroup A and Subgroup B. If Subgroup A is chosen as the reference group, then all primary studies in Subgroup A would be coded as 0, while those in Subgroup B would be coded as 1. Mathematically, this can be represented as C = 0 for Subgroup A and C = 1 for Subgroup B. The regression coefficient of C, \(\beta _1\), quantifies the effect size difference between the two subgroups. When C = 0, \(\beta _{0}\) becomes the true overall effect of Subgroup A. When C = 1, the overall effect of Subgroup B is captured by the sum \(\beta _{0}\) and \(\beta _{1}\). In summary, the observed effect size for the study i, \(ES_i\), is an estimator of the study’s true effect size, \(\beta _0\) + \(\beta _1\)\(C\) + \(\delta _i\), burdened by the sampling error, \(e_i\).
Eq. (17) is a mixed-effects meta-regression model, a standard choice for meta-regression. In subgroup analyses, this model combines the study effects within each subgroup using a random-effects model, while a fixed-effect model is used to combine subgroups and yield the overall effect (Borenstein et al., 2009). A Wald-type test is used in meta-regression to determine if the slope of the model is statistically significant, using the Z-score. In subgroup analyses, a statistically significant slope suggests that Subgroups A and B exhibit statistically significant differences between their overall effect sizes. In other words, the subgroup membership can explain some or all of the between-study heterogeneity. Another method to assess a moderator’s impact in meta-regression is through Cochran’s Q. In subgroup analyses, if the Q-statistic for the predictor is statistically significant, it means that the subgroup membership explains some or the entirety of the variability observed in the effect sizes. The \(R^{2}\) index can be employed in meta-regression to quantify the proportion of the true heterogeneity across all studies (i.e., the between-study heterogeneity) that can be accounted for by moderators.
In a meta-regression model with a single continuous moderator, as shown in Eq. (18) (Harrer et al., 2021), \begin {equation} ES_i ={\beta _0} + {\beta _1}x_i +\delta _i + e_i \label {18} \end {equation} \(x_i\) represent a continuous moderator, \(\beta _1\) is the regression slope. \(\delta _i\) and \(e_i\) are the between- and within-study error terms for the study i, respectively. \(\beta _0\) is still the model intercept, but it now represents the overall true effect size when x = 0. In summary, \(ES_i\) represents the observed effect size for the study i, which is an estimator of the study’s true effect size, \(\beta _0\) + \(\beta _1\)\(x_i\) + \(\delta _i\), burdened by the sampling error, \(e_i\).
As summarized by Harrer et al. (2021), meta-regression analyzes the relationship between predictors and observed effects to identify a consistent pattern between them, in the form of a regression line. By accounting for both sampling error and between-study differences, meta-regression seeks to fit a model that can generalize across all possible studies relevant to the topic. A well-fitting meta-regression model can predict effect sizes close to the observed data.
An important caveat
Moderator analysis is subject to several limitations that should be taken into consideration. A primary issue is that both the subgroup analysis and meta-regression require a large ratio of studies to moderators. It is generally recommended that moderator analysis should only be conducted when there are at least 10 studies available for each moderator included in the analysis. This is particularly crucial in multivariate models where the number of studies might be small, leading to reduced statistical power (Higgins & Green, 2006; Littell et al., 2008).
Another significant limitation is that the significant differences observed between subgroups of studies cannot be seen as causal evidence. We may fail to identify moderators that are truly responsible for the heterogeneity in effect sizes. Consequently, causal conclusions cannot be drawn solely from moderator analyses (Cuijpers, 2016; Littell et al., 2008). We strongly recommend that researchers select moderators based on solid theoretical reasoning and only test those moderators with a strong theoretical basis. This approach helps prevent erroneously attributing heterogeneity to spurious moderators (Schmidt & Hunter, 2014).
In a mixed-effects model meta-regression, the summary effect size for each subgroup is computed using a random-effects model. Instead of estimating \(\tau ^{2}\) across all studies, it’s estimated within these subgroups. In other words, each subgroup has its own estimated \(\tau ^2\). These \(\tau ^2\) estimates may vary across subgroups. We can choose to pool them or keep them separate when we compute the overall and within-subgroup summary proportions, depending on our assumptions (Borenstein et al., 2009).
If we attribute the differences in these observed within-group \(\tau ^{2}\) estimates solely to sampling error, then we anticipate a common \(\tau ^{2}\) across subgroups. In such a scenario, pooling a common \(\tau ^{2}\) estimate and applying it universally to all studies is appropriate. Conversely, if systematic factors, beyond just sampling errors, are believed to influence the varying values of the observed within-group \(\tau ^{2}\) estimates, then employing distinct \(\tau ^{2}\) estimates for each subgroup is justified. Essentially, using a separate estimate for between-study variance is equal to conducting an independent meta-analysis for each subgroup. It’s important to emphasize that the pooled proportion across all subgroups is likely to differ from the summary proportion derived from pooling across all studies without subgrouping. Nevertheless, any differences in these estimates are generally negligible.
When we assume that \(\tau ^{2}\) is the same for all subgroups, we can use the \(R^2\) index to represent the proportion of the between-study variance across all studies that can be explained by the subgroup membership (Borenstein et al., 2009).
We have developed the following generic code to help readers perform subgroup analyses and compute the overall and within-subgroup summary proportions. It is essential for readers to gain a thorough understanding of their data’s characteristics to choose the appropriate computational option.
In the first situation, we do not assume a common between-study variance component across subgroups and thus do not pool within-group \(\tau ^{2}\) estimates. In R, we first fit a random-effects model for each subgroup, and then we combine the estimated statistics into a data frame. In the next step, we fit a fixed-effect model to compare the two estimated logit transformed proportions and recalculate the summary proportion. The generic code is provided below:
# Assumption 1: # Do not assume a common between-study variance # component (not pooling within-group estimates of # between-study variance) # Option 1: no transformation # Conduct a random-effects model meta-analsis for each # subgroup defined by the moderator variable pes.subgroup1 <- rma(yi, vi, data = ies, subset = moderator == "subgroup1") pes.subgroup2 <- rma(yi, vi, data = ies, subset = moderator == "subgroup2") # Create a dataframe to store effect size estimates, # standard errors, heterogeneity for both subgroups # Add an object named moderator to distinguish two # subgroups. It will be used in the next step. dat.diffvar <- data.frame(estimate = c(pes.subgroup1$b, pes.subgroup2$b), stderror = c(pes.subgroup1$se, pes.subgroup2$se), moderator = c("subgroup1", "subgroup2"), tau2 = round(c(pes.subgroup1$tau2, pes.subgroup2$tau2), 3)) # Fit a fixed-effect meta-regression to compare the # subgroups subganal.moderator <- rma(estimate, sei = stderror, mods = ~ moderator, method = "FE", data = dat.diffvar) # Recalculate summary effect size assuming different # heterogeneity components pes.moderator <- rma(estimate, sei = stderror, method = "FE", data = dat.diffvar) pes.moderator <- predict(pes.moderator) # Display subgroup 1 summary effect size print(pes.subgroup1) # Display subgroup 2 summary effect size print(pes.subgroup2) # Display subgroup analysis results print(subganal.moderator) # Display recomputed summary effect size print(pes.moderator) # Option 2: the logit transformation # Conduct a random-effects model meta-analsis for each # subgroup defined by the moderator variable pes.logit.subgroup1 <- rma(yi, vi, data = ies.logit, subset = moderator == "subgroup1") pes.logit.subgroup2 <- rma(yi, vi, data = ies.logit, subset = moderator == "subgroup2") pes.subgroup1 <- predict(pes.logit.subgroup1, transf = transf.ilogit) pes.subgroup2 <- predict(pes.logit.subgroup2, transf = transf.ilogit) # Create a dataframe to store effect size estimates, # standard errors, heterogeneity for both subgroups # Add an object named moderator to distinguish two # subgroups. dat.diffvar <- data.frame(estimate = c(pes.logit.subgroup1$b, pes.logit.subgroup2$b), stderror = c(pes.logit.subgroup1$se, pes.logit.subgroup2$se), moderator = c("subgroup1", "subgroup2"), tau2 = round(c(pes.logit.subgroup1$tau2, pes.logit.subgroup2$tau2), 3)) # Fit a fixed-effect meta-regression to compare the # subgroups subganal.moderator <- rma(estimate, sei = stderror, mods = ~ moderator, method = "FE", data = dat.diffvar) # Recalculate summary effect size assuming different # heterogeneity components pes.logit.moderator <- rma(estimate, sei = stderror, method = "FE", data = dat.diffvar) pes.moderator <- predict(pes.logit.moderator, transf = transf.ilogit) # Display subgroup 1 summary effect size print(pes.subgroup1); print(pes.logit.subgroup1) # Display subgroup 2 summary effect size print(pes.subgroup2); print(pes.logit.subgroup2) # Display subgroup analysis results print(subganal.moderator) # Display recomputed summary effect size print(pes.moderator) # Option 3: the double arcsine transformation # Conduct a random-effects model meta-analsis for each # subgroup defined by the moderator variable # targ can also be set to list(ni = 1/(pes.da$se)^2) pes.da.subgroup1 <- rma(yi,vi,data = ies.da, subset = moderator == "subgroup1") pes.da.subgroup2 <- rma(yi,vi,data = ies.da, subset = moderator == "subgroup2") pes.subgroup1 <- predict(pes.da.subgroup1, transf = transf.ipft.hm,targ = list(ni = dat$total)) pes.subgroup2 <- predict(pes.da.subgroup2, transf = transf.ipft.hm,targ = list(ni = dat$total)) # Create a dataframe to store effect size estimates, # standard errors, heterogeneity for both subgroups # Add an object named moderator to distinguish two # subgroups. dat.diffvar <- data.frame(estimate = c(pes.da.subgroup1$b, pes.da.subgroup2$b), stderror = c(pes.da.subgroup1$se, pes.da.subgroup2$se), moderator = c("subgroup1", "subgroup2"), tau2 = round(c(pes.da.subgroup1$tau2, pes.da.subgroup2$tau2), 3)) # Fit a fixed-effect meta-regression to compare the # subgroups subganal.moderator <- rma(estimate, sei = stderror, mods = ~ moderator, method = "FE", data = dat.diffvar) # Recalculate summary effect size assuming different # heterogeneity components # targ can also be set to list(ni = 1/(pes.da$se)^2) pes.da.moderator <- rma(estimate, sei = stderror, method = "FE", data = dat.diffvar) pes.moderator <- predict(pes.da.moderator, transf = transf.ipft.hm, targ = list(ni = dat$total)) # Display subgroup 1 summary effect size print(pes.subgroup1); print(pes.da.subgroup1) # Display subgroup 2 summary effect size print(pes.subgroup2); print(pes.da.subgroup2) # Display subgroup analysis results print(subganal.moderator) # Display recomputed summary effect size print(pes.moderator)
In the second situation, we assume a common between-study variance component across subgroups and pool within-group \(\tau ^{2}\) estimates. Generally speaking, unless there is a substantial number of studies available within each subgroup (i.e., more than five studies) or compelling evidence suggesting within-group variances vary from one subgroup to the next, it is sufficient to calculate summary proportions and create forest plots with a pooled \(\tau ^{2}\) (Borenstein et al. (2009)). In this case, we can directly use the rma() function and fit a mixed-effects model to evaluate the potential moderator. In R, we still need to combine the estimated statistics into a new data frame for us to calculate a new overall summary proportion using a pooled \(\tau ^{2}\) across all studies.
# Assumption 2: Assume a common between-study variance # component (pool within-group estimates of # between-study variance) # Option 1: no transformation # Conduct moderator analysis subganal.moderator <- rma(yi, vi, data = ies, mods = ~ moderator) pes.subg.moderator <- predict(subganal.moderator) # Obtain estimates for each subgroup pes.subgroup1 <- rma(yi, vi, data = ies, mods = ~ moderator == "subgroup2") pes.subgroup2 <- rma(yi, vi, data = ies, mods = ~ moderator == "subgroup1") # Create a dataframe to store effect size estimates, # standard errors, heterogeneity for both subgroups dat.samevar <- data.frame(estimate = c((pes.subgroup1$b)[1], (pes.subgroup1$b)[1]), stderror = c((pes.subgroup2$se)[1], (pes.subgroup2$se)[1]), tau2 = subganal.moderator$tau2) # Recalculate summary effect size assuming a common # heterogeneity component pes.moderator <- rma(estimate, sei = stderror, method = "FE", data = dat.samevar) pes.moderator <- predict(pes.moderator) # Display subgroup 1 summary effect size print(pes.subg.moderator[study label 1]) # Display subgroup 2 summary effect size print(pes.subg.moderator[study label 2]) # Display subgroup analysis results print(subganal.moderator) # Display recomputed summary effect size print(pes.moderator) # Option 2: the logit transformation # Conduct moderator analysis subganal.moderator <- rma(yi, vi, data = ies.logit, mods = ~ moderator) pes.subg.moderator <- predict(subganal.moderator, transf=transf.ilogit) # Obtain estimates for each subgroup pes.logit.subgroup1 <- rma(yi, vi, data = ies.logit, mods = ~ moderator == "subgroup2") pes.logit.subgroup2 <- rma(yi, vi, data = ies.logit, mods =~ moderator == "subgroup1") # Create a dataframe to store effect size estimates, # standard errors, heterogeneity for both subgroups dat.samevar <- data.frame(estimate = c((pes.logit.subgroup1$b)[1],(pes.logit.subgroup2$b)[1]), stderror = c((pes.logit.subgroup1$se)[1],(pes.logit.subgroup2$se)[1]), tau2 = subganal.moderator$tau2) # Recalculate summary effect size assuming a common # heterogeneity component pes.logit.moderator <- rma(estimate, sei = stderror, method = "FE", data = dat.samevar) pes.moderator <- predict(pes.logit.moderator, transf = transf.ilogit) # Display subgroup 1 summary effect size print(pes.subg.moderator[study lable 1]) # Display subgroup 2 summary effect size print(pes.subg.moderator[study lable 2]) # Display subgroup analysis results print(subganal.moderator) # Display recomputed summary effect size print(pes.moderator) # Option 3: the double arcsine transformation # Conduct moderator analysis # targ can also be set to list(ni = 1/(pes.da$se)^2) subganal.moderator <- rma(yi, vi, data = ies.da, mods = ~ moderator) pes.subg.moderator <- predict(subganal.moderator, transf = transf.ipft.hm, targ = list(ni=dat$total)) # Obtain estimates for each subgroup pes.da.subgroup1 <- rma(yi, vi, data = ies.da, mods = ~ moderator == "subgroup2") pes.da.subgroup2 <- rma(yi, vi, data = ies.da, mods = ~ moderator == "subgroup1") # Create a dataframe to store effect size estimates, # standard errors, heterogeneity for both subgroups dat.samevar <- data.frame(estimate = c((pes.da.subgroup1$b)[1], (pes.da.subgroup2$b)[1]), stderror = c((pes.da.subgroup1$se)[1], (pes.da.subgroup2$se)[1]), tau2 = subganal.moderator$tau2) # Recalculate summary effect size assuming a common # heterogeneity component # targ can also be set to list(ni = 1/(pes.da$se)^2) pes.da.moderator <- rma(estimate, sei = stderror, method = "FE", data = dat.samevar) pes.moderator <- predict(pes.da.moderator, transf = transf.ipft.hm, targ = list(ni = dat$total)) # Display subgroup 1 summary effect size print(pes.subg.moderator[study lable 1]) # Display subgroup 2 summary effect size print(pes.subg.moderator[study lable 2]) # Display subgroup analysis results print(subganal.moderator) # Display recomputed summary effect size print(pes.moderator)
To help readers better understand how to use the code templates, we will now illustrate their implementation with the running example. For demonstrative purposes, we will use the variable “study design” (Birth cohort vs. Others) as the moderator and conduct the analysis with the logit transformation under both assumptions.
In the first situation, we do not assume a common between-study variance component across subgroups:
# Conduct a random-effects model meta-analsis for each # subgroup defined by the moderator studydesign pes.logit.birthcohort <- rma(yi, vi, data=ies.logit, subset=studydesign == "Birth cohort", method="DL") pes.logit.others <- rma(yi, vi, data=ies.logit, subset=studydesign == "Others", method = "DL") pes.birthcohort <- predict(pes.logit.birthcohort, transf = transf.ilogit, digits = 5) pes.others <- predict(pes.logit.others, transf = transf.ilogit, digits = 5) # Create a dataframe to store effect size estimates, # standard errors, heterogeneity for both subgroups # Add an object named studydesign to distinguish two # subgroups. dat.diffvar <- data.frame(estimate = c(pes.logit.birthcohort$b, pes.logit.others$b), stderror = c(pes.logit.birthcohort$se, pes.logit.others$se), studydesign = c("Birth cohort", "Others"), tau2 = round(c(pes.logit.birthcohort$tau2, pes.logit.others$tau2), 3)) # Fit a fixed-effect meta-regression to compare the # subgroups subganal.studydesign <- rma(estimate, sei = stderror, data = dat.diffvar, mods = ~ studydesign, method = "FE") # Recalculate summary effect size assuming different # heterogeneity components pes.logit.studydesign <- rma(estimate, sei = stderror, method = "FE", data = dat.diffvar) pes.studydesign <- predict(pes.logit.studydesign, transf = transf.ilogit) # Display summary effect sizes of the two subgroups print(pes.birthcohort, digits = 6); print(pes.logit.birthcohort, digits = 3) print(pes.others, digits = 6); print(pes.logit.others, digits = 3) # Display subgroup analysis results print(subganal.studydesign, digits = 3) # Display recomputed summary effect size print(pes.studydesign, digits = 6)
The outcomes of the subgroup analysis appear in Figure 13.
pred ci.lb ci.ub pi.lb pi.ub 0.000352 0.000158 0.000782 0.000045 0.002737 Random-Effects Model (k = 6; tau^2 estimator: DL) tau^2 (estimated amount of total heterogeneity): 0.932 (SE = 0.866) tau (square root of estimated tau^2 value): 0.966 I^2 (total heterogeneity / total variability): 98.55% H^2 (total variability / sampling variability): 68.92 Test for Heterogeneity: Q(df = 5) = 344.594, p-val < .001 Model Results: estimate se zval pval ci.lb ci.ub -7.952 0.408 -19.501 <.001 -8.752 -7.153 *** --- Signif. codes: 0 ’***’ 0.001 ’**’ 0.01 ’*’ 0.05 ’.’ 0.1 ’ ’ 1 pred ci.lb ci.ub pi.lb pi.ub 0.000472 0.000341 0.000653 0.000169 0.001317 Random-Effects Model (k = 11; tau^2 estimator: DL) tau^2 (estimated amount of total heterogeneity): 0.247 (SE = 0.175) tau (square root of estimated tau^2 value): 0.497 I^2 (total heterogeneity / total variability): 95.76% H^2 (total variability / sampling variability): 23.59 Test for Heterogeneity: Q(df = 10) = 235.944, p-val < .001 Model Results: estimate se zval pval ci.lb ci.ub -7.658 0.166 -46.161 <.001 -7.984 -7.333 *** --- Signif. codes: 0 ’***’ 0.001 ’**’ 0.01 ’*’ 0.05 ’.’ 0.1 ’ ’ 1 Fixed-Effects with Moderators Model (k = 2) I^2 (residual heterogeneity / unaccounted variability): 0.00% H^2 (unaccounted variability / sampling variability): 1.00 R^2 (amount of heterogeneity accounted for): NA% Test for Residual Heterogeneity: QE(df = 0) = 0.000, p-val = 1.000 Test of Moderators (coefficient 2): QM(df = 1) = 0.445, p-val = 0.505 Model Results: estimate se zval pval ci.lb ci.ub intrcpt -7.952 0.408 -19.501 <.001 -8.752 -7.153 *** studydesignOthers 0.294 0.440 0.667 0.505 -0.569 1.157 --- Signif. codes: 0 ’***’ 0.001 ’**’ 0.01 ’*’ 0.05 ’.’ 0.1 ’ ’ 1 pred ci.lb ci.ub 0.000453 0.000335 0.000611
From the output above, we can derive that the summary effect estimates are 0.00035 (95% CI = 0.00016, 0.00078), 0.00047 (95% CI = 0.00034, 0.00065), and 0.00045 (95% CI = 0.00034, 0.00061) for the two subgroups and the overall group of studies, respectively. Note that the subgroup summary effect estimates are derived by taking the exponential of the model results (e.g., exp(-7.952) = 0.00035). When we fit separate random-effects models in the two subgroups, we decide to allow the amount of variance within each set of studies to be different, which results in two different within-group estimates of \(\tau ^{2}\) (0.93 and 0.25 for studies using the birth cohort design and other study designs, respectively). In other words, studies within each subgroup share the same estimate of \(\tau ^{2}\) .
The results reveal that the difference between the two subgroup summary estimates is not statistically significant (QM(1) = 0.45, p = 0.51). Note that the sum of the within-group heterogeneity across the subgroups in the fixed-effect model is equal to QE(0) = 0, p = 1. This is because the within-group heterogeneity has been accounted for in each subgroup (Q(df = 5) = 344.594, p < 0.001; Q(df = 10) = 235.944, p < 0.01, respectively) in the random-effects model, thus there is no heterogeneity left to be accounted for.
In the second situation where we assume a common between-study variance component across subgroups, execute the following code:
# Conduct a subgroup analysis based on studydesign subganal.studydesign <- rma(yi, vi, data = ies.logit, mods = ~ studydesign, method = "DL") pes.subg.studydesign <- predict(subganal.studydesign, transf = transf.ilogit) # Obtain estimates for each subgroup pes.logit.birthcohort <- rma(yi, vi, data = ies.logit, mods = ~ studydesign == "Others", method = "DL") pes.logit.others = rma(yi, vi, data = ies.logit, mods = ~ studydesign == "Birth cohort", method = "DL") # Create a dataframe to store effect size estimates, # standard errors, heterogeneity for both subgroups dat.samevar <- data.frame(estimate = c((pes.logit.birthcohort$b)[1], (pes.logit.others$b)[1]), stderror = c((pes.logit.birthcohort$se)[1], (pes.logit.others$se)[1]), tau2 = subganal.studydesign$tau2) # Recalculate summary effect size assuming a common # heterogeneity component pes.logit.studydesign = rma(estimate, sei = stderror, method = "FE", data = dat.samevar) pes.studydesign = predict(pes.logit.studydesign, transf = transf.ilogit) # Display subgroup summary effect sizes print(pes.subg.studydesign[1], digits = 6) print(pes.subg.studydesign[17], digits = 6) # Display subgroup analysis results print(subganal.studydesign, digits = 4) # Display recomputed summary effect size print(pes.studydesign, digits = 6)
The outcome of the subgroup analysis appears in Figure 14. This output is fairly self-explanatory. Based on this output, we can derive that we have fitted a mixed-effects model, meaning a random-effects model is used to combine studies within each subgroup and a fixed-effect model is used to combine the subgroups and estimate the summary effect size. The amount of within-group heterogeneity across the two subgroups is assumed to be the same (\(\tau ^{2}\) = 0.44 in this case). This combined estimate is derived by pooling the two within-group variance estimates as displayed earlier (\(\tau ^{2}\) = 0.93 and \(\tau ^{2}\) = 0.25). Once we have the pooled estimate, we then apply it to each study across the two subgroups, meaning every study now shares the same estimate of \(\tau ^{2}\) (i.e., 0.44).
Mixed-Effects Model (k = 17; tau^2 estimator: DL) tau^2 (estimated amount of residual heterogeneity): 0.4427 (SE = 0.2518) tau (square root of estimated tau^2 value): 0.6654 I^2 (residual heterogeneity / unaccounted variability): 97.42% H^2 (unaccounted variability / sampling variability): 38.70 R^2 (amount of heterogeneity accounted for): 0.00% Test for Residual Heterogeneity: QE(df = 15) = 580.5386, p-val < .0001 Test of Moderators (coefficient 2): QM(df = 1) = 0.9202, p-val = 0.3374 Model Results: estimate se zval pval ci.lb ci.ub intrcpt -7.9742 0.2892 -27.5726 <.0001 -8.5411 -7.4074 *** studydesignOthers 0.3452 0.3599 0.9593 0.3374 -0.3601 1.0506 --- Signif. codes: 0 ’***’ 0.001 ’**’ 0.01 ’*’ 0.05 ’.’ 0.1 ’ ’ 1 pred ci.lb ci.ub pi.lb pi.ub 1 0.000344 0.000195 0.000606 0.000083 0.001425 pred ci.lb ci.ub pi.lb pi.ub 17 0.000486 0.000319 0.000739 0.000124 0.001910 pred ci.lb ci.ub 0.000430 0.000307 0.000602
The test of moderators suggests that the study design does not have a moderating effect (QM(1) = 0.92, p = 0.34). That is, when we divide the included studies according to their study designs, we fail to find any significant differences between the two subgroups of effect sizes. This conclusion is also supported by the results of the test for residual heterogeneity: there is significant unexplained heterogeneity left in the effect sizes (QE(15) = 580.54, p < 0.01), which can also explain why \(R^{2}\) shows 0%. Finally, the estimates for the two subgroup summary proportions and the overall summary proportion are displayed at the bottom of the output. They are 0.00034 (95% CI = 0.0002, 0.00061), 0.00049 (95% CI = 0.00032, 0.00074), and 0.00043 (95% CI = 0.00031, 0.0006), respectively.
There are several other points that are worth noting. Under the framework of the mixed-effect model, the residual heterogeneity estimate here (QE(15) = 580.54) is the sum of the two within-group heterogeneity estimates we have obtained above in the random-effects model (Q(df = 5) = 344.59, Q(df = 10) = 235.94, respectively). When we dummy-code a moderator with two categories, the subset of studies coded as 0 in a dummy variable will function as the reference group, represented by the intercept of the fitted mixed-effects regression model. The other subset of studies coded as 1 will be compared against the reference group. In the running example, the “Birth cohort” group is the reference group, while the “Others” group is compared against it. The estimate of the intercept (i.e., -7.97) is the logit-transformed summary effect size of the reference group (i.e, logit(0.00034)). The slope is estimated to be 0.35. The sum of the slope and the intercept is equal to -7.629, which is the logit-transformed summary effect size of the “Others” group (i.e., logit(0.00049)).
When calculating the summary effect estimate across the subgroups, the outcomes may vary depending on the specific \(\tau ^{2}\) estimate applied. However, even with this variation, the two computational models may reach the same qualitative conclusions. For instance, in the given example, both models agree that the study design doesn’t significantly influence the results. In general, Borenstein et al. (2009) recommend pooling the separate \(\tau ^{2}\) when the number of studies in a subgroup is small (i.e., less than five studies). In doing so, we can obtain a more accurate estimate of \(\tau ^{2}\). In contrast, if we decide not to pool them, each subgroup should ideally consist of at least five studies to ensure moderately stable estimates of \(\tau ^{2}\).
Many authors conducting meta-analyses of proportions did not construct forest plots correctly for their subgroup analyses. Specifically, numerous published meta-analytic studies did not present the appropriate estimates for either the overall or subgroup summary proportions in their forest plots. These authors failed to consider the two possible assumptions about \(\tau ^2\) that we have discussed in Section 7.3.
In this section, we will construct forest plots with subgroups under different assumptions (i.e., separate between-study variance components vs. a common between-study variance component). We have obtained the estimates for subgroup and overall summary proportions in the previous section, which can be used to create our forest plots. The following code is used to construct forest plots under the first assumption:
# Assumption 1: Do not assume a common between-study # variance component (use separate within-group # estimates of between-study variance). # Option 1: no transformation ies.summary <- summary(ies, ni = dat$total) forest(ies.summary$yi, ci.lb = ies.summary$ci.lb, ci.ub = ies.summary$ci.ub, rows = c(d:c, b:a)) # Option 2: the logit transformation ies.summary <- summary(ies.logit, transf = transf.ilogit) forest(ies.summary$yi, ci.lb = ies.summary$ci.lb, ci.ub = ies.summary$ci.ub, rows = c(d:c, b:a)) # Option 3: the double arcsine transformation ies.summary <- summary(ies, transf = transf.ipft, ni = dat$total) forest(ies.summary$yi, ci.lb = ies.summary$ci.lb, ci.ub = ies.summary$ci.ub, rows = c(d:c, b:a))
The code above merely builds the “bones” of a forest plot. More components need to be added to it (e.g., texts, headers, labels, etc.). We also have to manually adjust its appearance to make it look more professional. Dividing a set of included studies into several subgroups in a forest plot using metafor has to be done manually with the rows argument. Readers may have noticed that the parameters in the argument (\(a\), \(b\), \(c\), and \(d\) denotes a particular position on the Y -axis) are ordered from right to left. \(a\) specifies the vertical position for plotting the first study in the first subgroup; \(b\) specifies the vertical position for plotting the last study in the first subgroup; \(c\) specifies the vertical position for plotting the first study in the second subgroup; \(d\) specifies the vertical position for plotting the last study in the second subgroup. Mathematically speaking, \(b-a+1\) and \(d-c+1\) should be equal to the number of studies in their corresponding subgroups. c and b do not need to be consecutive numbers. If we order these parameters from left to right, studies will be displayed in reverse order with the first study being displayed at the bottom of the plot and the last study being displayed at the top of all the studies.
To illustrate, we can execute the following code to create a forest plot using the study design as the moderator:
# Run the subgroup analysis code with the assumption # of separate within-group estimates of between-study # variance components first, then run the following # code ies.summary <- summary(ies.logit, transf = transf.ilogit) # par() function specifies font parameters par(cex = 1, font = 6) # Set up forest plot # order= argument ensures that studies are divided by # the subgroup variable forest(ies.summary$yi, order = ies.summary$studesg, ci.lb = ies.summary$ci.lb, ci.ub = ies.summary$ci.ub, ylim = c(-5, 23), xlim = c(-0.005, 0.005), slab = paste(dat$author, dat$year, sep = ","), ilab = cbind(data = dat$cases, dat$total), ilab.xpos = c(-0.0019, -0.0005), ilab.pos = 2, rows = c(19:14, 8.5:-1.5), at = c(seq(from = 0, to = 0.004, by = 0.001)), refline = pes.studydesign$pred, main = "", xlab = "Proportion", digits = 4) # Add summary polygons for the subgroup and overall # proportions par(cex = 1.2, font = 7) addpoly(pes.birthcohort$pred, ci.lb = pes.birthcohort$ci.lb, ci.ub = pes.birthcohort$ci.ub, row = 12.8, digits = 5) addpoly(pes.others$pred, ci.lb = pes.others$ci.lb, ci.ub = pes.others$ci.ub, row = -2.7, digits = 5) addpoly(pes.studydesign$pred, ci.lb = pes.studydesign$ci.lb, ci.ub = pes.studydesign$ci.ub, row = -4.6, digits = 5) # Add column headings to the plot par(cex = 1.1, font = 7) text(-0.005, 21.8, pos = 4, "Study") text(c(-0.0026, -0.0014), 21.8, pos = 4, c("Cases", "Total")) text(0.0025, 21.8, pos = 4, "Proportion [95% CI]") # Add text for the subgroups text(-0.005, c(9.7, 20.2), pos = 4, c("Others", "Birth cohort")) # Add text for the subgroup and overall proportions par(cex = 1, font = 7) text(-0.005, -4.6, pos = 4, c("Overall proportion")) text(-0.005, 12.8, pos = 4, c("Subgroup proportion")) text(-0.005, -2.7, pos = 4, c("Subgroup proportion")) abline(h = -3.7)
The generated forest plot is shown in Figure 15. Notice that the overall summary proportion is 0.00045 (95% CI = 0.00033, 0.00061) under the given assumption, which is different than the one derived in the absence of subgroups (0.00042).
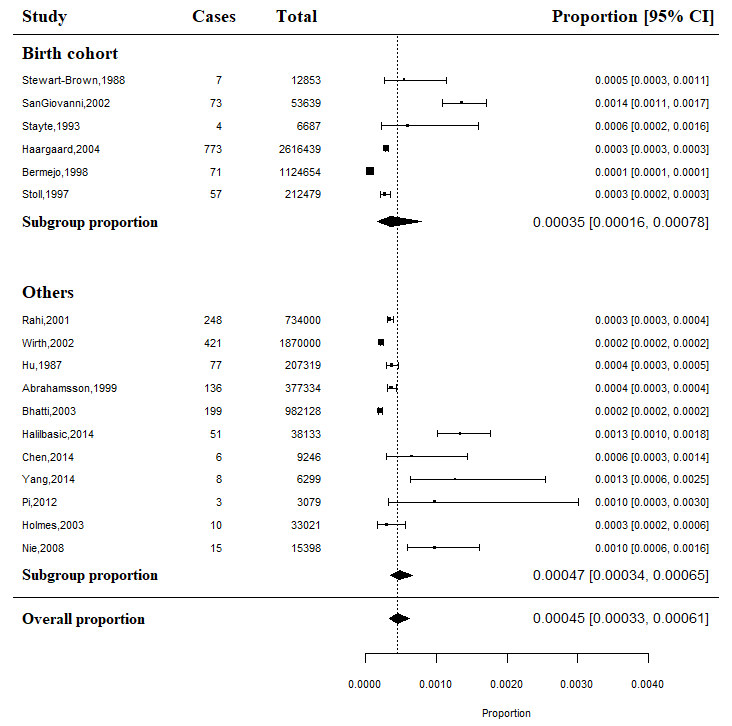
Under the assumption of a common \(\tau ^{2}\), we employ the rma() function in metafor in conjunction with the metaprop() and forest() functions in meta to produce a forest plot with subgroups. The inclusion of predictors is set by the mods argument in metafor and the byvar argument in meta. In the metaprop() function, two arguments are particularly noteworthy: tau.common determines whether a common \(\tau ^2\) estimate is applied across subgroups, while tau.preset sets the value of \(\tau \). Given our assumption, we set tau.common to TRUE and tau.preset to the pooled \(\tau \) estimate obtained from the previous section.
# Assumption 2: Assume a common between-study variance # component (pooling within-group estimates of # between-study variance) # data= could also be set to ies.logit or ies.da subganal.moderator <- rma(yi, vi, data = ies, mods = ~ moderator, method = "DL") # sm= could also be set to "PLO" or "PFT" # tau.common= must be TRUE and tau.preset must be # sqrt(subganal.moderator$tau2) pes.summary <- metaprop(cases, total, authoryear, data = dat, sm = "PRAW", byvar = moderator, tau.common=TRUE, tau.preset = sqrt(subganal.moderator$tau2)) # resid.hetstat= must be FALSE forest(pes.summary, resid.hetstat = FALSE)
Assuming that we apply a common \(\tau ^{2}\) across subgroups, the following code creates a customized forest plot using the study design as the moderator:
subganal.studydesign <- rma(yi, vi, data = ies.logit, mods = ~ studydesign, method = "DL") pes.summary <- metaprop(cases, total, authoryear, data = dat, sm = "PLO", method.tau = "DL", method.ci = "NAsm", byvar = studydesign, tau.common=TRUE, tau.preset = sqrt(subganal.studydesign$tau2)) forest(pes.summary, common = FALSE, overall = TRUE, overall.hetstat = TRUE, resid.hetstat = FALSE, subgroup.hetstat = TRUE, test.subgroup = FALSE, fs.hetstat = 10, print.tau2 = TRUE, print.Q = TRUE, print.pval.Q = TRUE, print.I2 = TRUE, rightcols = FALSE, xlim = c(0 ,4), leftcols = c("studlab", "effect", "ci"), leftlabs = c("Study", "Proportion", "95% C.I."), text.random.w = "Subgroup proportion", text.random = "Overall proportion", xlab = "Prevalence of CC (%)", pscale = 1000, smlab = " ", weight.study = "random", squaresize = 0.5, col.square = "navy", col.diamond = "maroon", col.diamond.lines = "maroon", digits = 2)
The generate forest plot is presented in Figure 16:
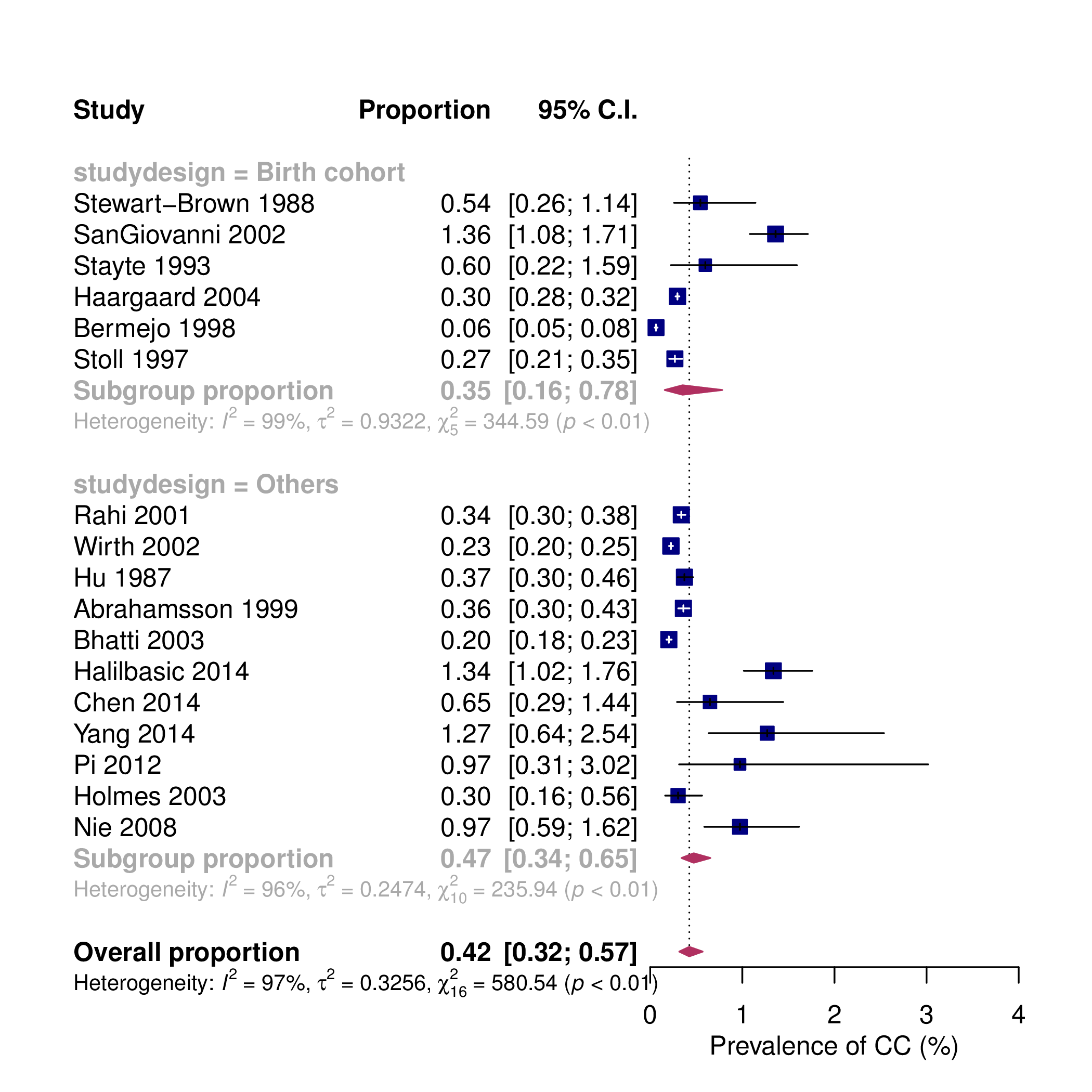
Notice that the estimates of \(\tau ^{2}\) are identical (0.4427) across two subgroups. The overall summary proportion and its 95% CI (0.43; 95% CI = 0.31, 0.6) are calculated across two subgroups based on the same \(\tau ^{2}\) estimate, as well.
When we want to evaluate the influence of a continuous moderator, the R code is identical to what we used for subgroup analyses:
#data= could also be set to ies.logit or ies.da metareg.moderator <- rma(yi, vi, data = ies, mods = ~ moderator)
As mentioned above, a mix of continuous and categorical moderators can be regressed on the effect sizes in a meta-regression model. This can be achieved by using the plus sign in the mods argument:
#data= could also be set to ies.logit or ies.da metareg.moderators <- rma(yi, vi, data = ies, mods = ~moderatorA + moderatorB + moderatorC + ...)
Scatter plots serve as an invaluable visualization tool when assessing potential moderator variables. Such plots, as depicted in Figure 17, are constructed with a regression line, flanked by two curved dotted lines that represent the 95% confidence interval bounds, with studies represented by circles drawn proportional to their study weights (i.e., larger studies appear as larger circles). What’s important in scatter plots is the slope of the regression line. Specifically, if the regression line is horizontal or nearly so, it suggests there’s no significant association between the moderator and the effect sizes. Conversely, if the regression line has a noticeable slope, it indicates the effect sizes change in relation to the value of the moderator. To determine the significance of this relationship, one can look at the slope and its significance test. A notably positive or negative slope indicates that the predictor plays a significant moderating role, potentially explaining a significant portion of the observed heterogeneity.
In this section, we will employ the regplot() function in the metafor package to create scatter plots. regplot() offers a distinct advantage over R’s native plot() function. It simplifies the coding process, making it more user-friendly, especially for those less familiar with R. It helps users to customize their scatter plots with ease.
The following generic code creates weighted scatter plots for subgroup analyses. In a weighted scatter plot, a study is represented by a circle. The weight of a study is depicted by the size of the circle, with a larger circle indicating a greater study weight. In an unweighted scatter plot, the circles are of equal size. Additionally, it is necessary to use dummy variables for categorical moderators (e.g., variables labeled as “studesg” in the running example).
# Option 1: no transformation regplot(subganal.dummyvar, mod = "dummyvar") # Option 2: the logit transformation regplot(metareg.dummyvar, mod = "dummyvar", transf=transf.ilogit) # Option 3: the double arcsine transformation # targ can also be set to list(ni = 1/(pes.da$se)^2) regplot(subganal.dummyvar, mod = "dummyvar", transf=transf.ipft.hm, targ=list(ni=dat$total))
Using the running example, we can create a customized scatter plot with a regression line and corresponding 95% CI bounds for “studesg” with the following code:
# Conduct a subgroup analysis based on the dummy # variable "studesg" subganal.studesg=rma (yi, vi, data = ies.logit, mods = ~ studesg, method = "DL") # Create a scatter plot regplot(subganal.studesg, mod = "studesg", xlab = "Study Design", transf=transf.ilogit, legend = FALSE, label = TRUE, shade = "white", bg = "transparent", lcol = "navy", digits = 4)
The generated scatter plot is shown in Figure 18.
Upon visual inspection of the scatter plot, it is evident that the slope of the estimated regression line is neither entirely horizontal nor excessively steep, suggesting a weak association between the study design and the observed effects. Furthermore, nearly half of the studies fall outside of the 95% CI bounds, indicating the presence of potentially unidentified moderators.7
In the second example, we use the sample size as the moderator (the variable “size” in the provided data set) and evaluate it in a subgroup analysis:
subganal.size <- rma(yi, vi, data = ies.logit, mods = ~ size, method = "DL") regplot(subganal.size, mod = "size", transf=transf.ilogit, xlab = "Sample size", legend = "topright", label = TRUE, shade = "white", bg = "transparent", lcol = "navy", digits = 6)
The generated scatter plot is presented in Figure 19. The code is self-explanatory. Note that the legend argument determines if a legend is added to the scatter plot, with its location specified by the user.
In this case, the estimated regression line exhibits a noticeably steeper slope. A visual inspection of this scatter plot indicates a negative correlation between the sample size and the observed proportions. When the sample size is less than 100,000, the proportions tend to be higher; when the sample size is larger than 100,000, the proportions tend to be lower. Again, it is important to acknowledge that potential missing moderators may introduce a degree of omitted variable bias here. The outcomes of the subgroup analysis are shown below in Figure 20.
Mixed-Effects Model (k = 17; tau^2 estimator: DL) tau^2 (estimated amount of residual heterogeneity): 0.1398 (SE = 0.0911) tau (square root of estimated tau^2 value): 0.3739 I^2 (residual heterogeneity / unaccounted variability): 93.90% H^2 (unaccounted variability / sampling variability): 16.40 R^2 (amount of heterogeneity accounted for): 57.07% Test for Residual Heterogeneity: QE(df = 15) = 246.0073, p-val < .0001 Test of Moderators (coefficient 2): QM(df = 1) = 36.4266, p-val < .0001 Model Results: estimate se zval pval ci.lb ci.ub intrcpt -7.0500 0.1643 -42.9109 <.0001 -7.3720 -6.7280 *** size -1.2867 0.2132 -6.0354 <.0001 -1.7046 -0.8689 *** --- Signif. codes: 0 ’***’ 0.001 ’**’ 0.01 ’*’ 0.05 ’.’ 0.1 ’ ’ 1
The results of the test of moderators (QM(1) = 36.43, p < 0.0001) as well as the significant regression coefficient (\(-\)1.29; Z(15) = \(-\)6.04, p < 0.0001) are consistent with our visual interpretation. In stark contrast with the previous subgroup analysis, the \(R^{2}\) indicates that 57.07% of the true heterogeneity in the observed effect size can be explained by the sample size.
In the running example, Wu et al. (2012) did not examine any continuous predictors. To demonstrate how to generate a weighted scatter plot for a meta-regression with a continuous predictor in R, we will plot the observed effect sizes against the year of publication, represented by the “year” variable in the provided dataset. The code is provided below:
metareg.year <- rma(yi, vi, data = ies.logit, mods = ~ year, method = "DL") regplot(metareg.year, mod = "year", transf = transf.ilogit, xlab = "Year of publication", legend = "topleft", label = TRUE, shade = "white", bg = "white", lcol = "navy", digits = 6)
The generated scatter plot is presented in Figure 21.
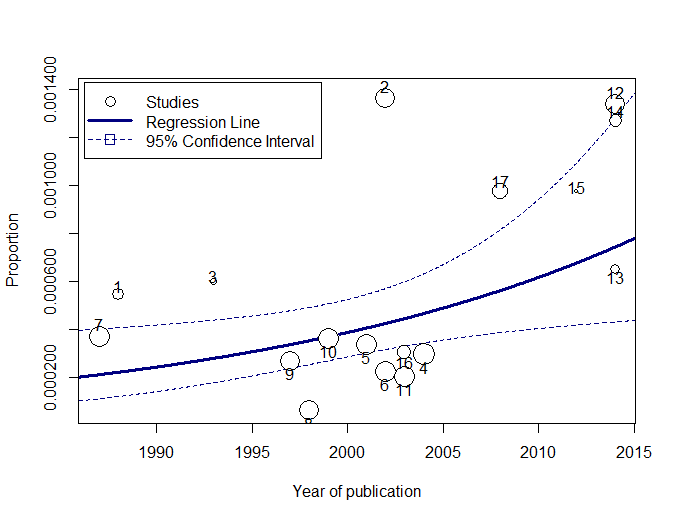
One of the major threats to the validity of meta-analysis is publication bias. This is a phenomenon where journals tend to accept and publish a study depending on the direction or strength of its results (MarksAnglin & Chen, 2020). Compared with studies with statistically significant results, small studies reporting insignificant results or small effects are less likely to be published and subsequently included in a meta analysis (Dickersin, 1990; Littell et al., 2008). Omitting unpublished studies in a systematic review could lead to a biased meta-analytic estimate of the summary effect (Song, Eastwood, Gilbody, Duley, & Sutton, 2000). As smaller studies require larger effect sizes to achieve statistical significance (Sterne, Gavaghan, & Egger, 2000), only those small studies with large effects get published and included in a relevant meta-analysis. Thus, a meta-analysis that only includes studies with large effects and fails to include studies with small effects at the same time could overestimate the true effect (Cuijpers, 2016).
Current methods of detecting publication bias and assessing its impact are developed for meta-analyses of randomized control trials. These methods rely on certain assumptions (Borenstein et al., 2009). Firstly, regardless of the significance of their effects, large studies are most likely to be published. Secondly, only small studies demonstrating significant and substantial effects tend to be published. Lastly, most moderate-scale studies that yield significant results also tend to be published. Consequently, as the sample size of a study decreases, the likelihood of it being affected by publication bias increases. Traditional methods such as trim-and-fill, the rank correlation test, Egger’s regression model, as well as the more sophisticated weighted selection approaches (e.g., Vevea & Hedges, 1995; Vevea & Woods, 2005) have all operated under the assumption that the publication likelihood depends on sample size, statistical significance, or the direction of results (Coburn & Vevea, 2015).
While empirical research has confirmed the dominant role of statistical significance in study publication (Preston, Ashby, & Smyth, 2004), the actual publication selection process across different fields is much more intricate. Cooper, DeNeve, and Charlton (1997) have demonstrated that decisions regarding study publication are influenced by various criteria or “filters” set by journal editors and reviewers, independent of methodological quality and significance. These filters can include factors such as research funding sources, societal preferences related to race and gender during the study’s conduction, and even findings that challenge pre-existing beliefs. Consequently, the traditional methods may fail to capture the full complexity of the publication selection process.
In practice, authors of meta-analyses of proportions have employed these methods in their attempts to detect publication bias. However, studies included in meta-analyses of proportions are observational and non-comparative. In other words, they only report a proportion or prevalence of an event, which inherently precludes the testing of statistical significance for their findings (Borenstein, 2019). Consequently, the interpretation of the outcomes from such studies is not contingent on the null hypothesis significance test and thus cannot be categorized as either “positive/negative” or “desirable/undesirable.” The significance levels are, therefore, unlikely to influence publication decisions regarding these studies (Maulik, Mascarenhas, Mathers, Dua, & Saxena, 2011). Authors who report low proportions (e.g., rare event rates) are equally likely to have their work published as those reporting very high proportions (e.g., high cure rates), given that the study quality meets rigorous publication standards. Consequently, the traditional publication bias assessment procedures may struggle to identify publication bias in meta-analyses of proportions, as bias in non-comparative studies can be introduced for reasons unrelated to statistical significance.
Borenstein (2019) warns meta-analysts that it is a mistake to apply publication bias procedures to studies of prevalence. Our suggestion aligns with his. When conducting meta-analyses of proportions, we believe that the traditional publication bias tests and modeling tools developed for randomized controlled trials have limited utility and, therefore, should not be used. Any conclusions drawn regarding the presence of publication bias based on these methods should be approached with caution.
Agresti, A., & Coull, B. A. (1998). Approximate is better than “exact” for interval estimation of binomial proportions. The American Statistician, 52(2), 119–126. doi: https://doi.org/10.2307/2685469
Anzures-Cabrera, J., & Higgins, J. P. (2010). Graphical displays for meta-analysis: An overview with suggestions for practice. Research Synthesis Methods, 1(1), 66–80. doi: https://doi.org/10.1002/jrsm.6
Barendregt, J. J., Doi, S. A., Lee, Y. Y., Norman, R. E., & Vos, T. (2013). Meta-analysis of prevalence. Journal of Epidemiology and Community Health, 67(11), 974–978. doi: https://doi.org/10.1136/jech-2013-203104
Borenstein, M. (2019). Common mistakes in meta-analysis and how to avoid them. Biostat.
Borenstein, M., Hedges, L., Higgins, J., & Rothstein, H. (2005). Comprehensive meta-analysis version 2. Biostat.
Borenstein, M., Hedges, L. V., Higgins, J., & Rothstein, H. R. (2009). Introduction to meta-analysis. John Wiley & Sons. doi: https://doi.org/10.1002/9781119558378
Borenstein, M., Hedges, L. V., Higgins, J. P., & Rothstein, H. R. (2010). A basic introduction to fixed-effect and random-effects models for meta-analysis. Research synthesis methods, 1(2), 97–111. doi: https://doi.org/10.1002/jrsm.12
Borenstein, M., Higgins, J. P., Hedges, L. V., & Rothstein, H. R. (2017). Basics of meta-analysis: \({I}^2\) is not an absolute measure of heterogeneity. Research synthesis methods, 8(1), 5–18.
Box, G. E., Hunter, J. S., & Hunter, W. G. (2005). Statistics for experimenters: design, innovation, and discovery (Vol. 2). Wiley-Interscience.
Card, N. A. (2015). Applied meta-analysis for social science research. Guilford Publications.
Chung, Y., Rabe-Hesketh, S., & Choi, I. H. (2013). Avoiding zero between-study variance estimates in random-effects meta-analysis. Statistics in Medicine, 32(23), 4071–4089. doi: https://doi.org/10.1002/sim.5821
Coburn, K. M., & Vevea, J. L. (2015). Publication bias as a function of study characteristics. Psychological Methods, 20(3), 310–330. doi: https://doi.org/10.1037/met0000046
Cochran, W. G. (1954). The combination of estimates from different experiments. Biometrics, 10(1), 101–129. doi: https://doi.org/10.2307/3001666
Cooper, H., DeNeve, K., & Charlton, K. (1997). Finding the missing science: The fate of studies submitted for review by a human subjects committee. Psychological Methods, 2(4), 447–452. doi: https://doi.org/10.1037/1082-989x.2.4.447
Cornell, J. E., Mulrow, C. D., Localio, R., Stack, C. B., Meibohm, A. R., Guallar, E., & Goodman, S. N. (2014). Random-effects meta-analysis of inconsistent effects: a time for change. Annals of Internal Medicine, 160(4), 267–270. doi: https://doi.org/10.7326/m13-2886
Cuijpers, P. (2016). Meta-analyses in mental health research: A practical guide. Pim Cuijpers Uitgeverij.
Davey, J., Turner, R. M., Clarke, M. J., & Higgins, J. P. (2011). Characteristics of meta-analyses and their component studies in the cochrane database of systematic reviews: a cross-sectional, descriptive analysis. BMC Medical Research Methodology, 11(1), 1–11. doi: https://doi.org/10.1186/1471-2288-11-160
Del Re, A. C. (2015). A practical tutorial on conducting meta-analysis in R. The Quantitative Methods for Psychology, 11(1), 37–50. doi: https://doi.org/10.20982/tqmp.11.1.p037
DerSimonian, R., & Laird, N. (1986). Meta-analysis in clinical trials. Controlled Clinical Trials, 7(3), 177–188. doi: https://doi.org/10.1016/0197-2456(86)90046-2
Dickersin, K. (1990). The existence of publication bias and risk factors for its occurrence. JAMA, 263(10), 1385–1389. doi: https://doi.org/10.1001/jama.1990.03440100097014
Egger, M., Schneider, M., & Smith, G. D. (1998). Spurious precision? meta-analysis of observational studies. British Medical Journal, 316(7125), 140–144.
Evangelou, E., & Veroniki, A. A. (2022). Meta-research: Methods and protocols. Springer.
Feng, C., Wang, H., Lu, N., Chen, T., He, H., Lu, Y., & Tu, X. M. (2014). Log-transformation and its implications for data analysis. Shanghai Archives of Psychiatry, 26(2), 105–109.
Freeman, M. F., & Tukey, J. W. (1950). Transformations related to the angular and the square root. Annals of Mathematical Statistics, 21(4), 607–611. doi: https://doi.org/10.1214/aoms/1177729756
Fusar-Poli, P., Schultze-Lutter, F., Cappucciati, M., Rutigliano, G., Bonoldi, I., Stahl, D., & Woods, S. W. (2015). The dark side of the moon: meta-analytical impact of recruitment strategies on risk enrichment in the clinical high risk state for psychosis. Schizophrenia Bulletin, 42(3), 732–743. doi: https://doi.org/10.1093/schbul/sbv162
Gillen, S., Schuster, T., Meyer Zum Bschenfelde, C., Friess, H., & Kleeff, J. (2010). Preoperative/neoadjuvant therapy in pancreatic cancer: a systematic review and meta-analysis of response and resection percentages. Plos Medicine, 7(4), e1000267–e1000267. doi: https://doi.org/10.1371/journal.pmed.1000267
Hamza, T. H., van Houwelingen, H. C., & Stijnen, T. (2008). The binomial distribution of meta-analysis was preferred to model within-study variability. Journal of Clinical Epidemiology, 61(1), 41–51. doi: https://doi.org/10.1016/j.jclinepi.2007.03.016
Hardy, R. J., & Thompson, S. G. (1998). Detecting and describing heterogeneity in meta-analysis. Statistics in Medicine, 17(8), 841–856. doi: 3.0.co;2-d" >https://doi.org/10.1002/(sici)1097-0258(19980430)17:8¡841::aid-sim781¿3.0.co;2-d
Harrer, M., Cuijpers, P., A, F. T., & Ebert, D. D. (2021). Doing meta-analysis with R: A hands-on guide (1st ed.). Boca Raton, FL and London: Chapman & Hall/CRC Press. doi: https://doi.org/10.1201/9781003107347
Hedges, L. V., & Olkin, I. (1985). Statistical methods for meta-analysis. Academic Press. doi: https://doi.org/10.2307/2289186
Hedges, L. V., & Vevea, J. L. (1998). Fixed-and random-effects models in meta-analysis. Psychological methods, 3(4), 486. doi: https://doi.org/10.1037/1082-989x.3.4.486
Higgins, J. P., & Green, S. (2006). Cochrane handbook for systematic reviews of interventions 4.2. 6 [updated september 2006]. The cochrane library, 4, 2006.
Higgins, J. P., & Thompson, S. G. (2002). Quantifying heterogeneity in a meta-analysis. Statistics in Medicine, 21(11), 1539–1558. doi: https://doi.org/10.1002/sim.1186
Higgins, J. P., Thompson, S. G., Deeks, J. J., & Altman, D. G. (2003). Measuring inconsistency in meta-analyses. British Medical Journal, 327(7414), 557–560. doi: https://doi.org/10.1136/bmj.327.7414.557
Huedo-Medina, T. B., Snchez-Meca, J., Marn-Martnez, F., & Botella, J. (2006). Assessing heterogeneity in meta-analysis: Q statistic or \({I}^2\) index? Psychological methods, 11(2), 193–206. doi: https://doi.org/10.1037/1082-989x.11.2.193
Hunter, J., Saratzis, A., Sutton, A. J., Boucher, R. H., Sayers, R. D., & Bown, M. J. (2014). In meta-analyses of proportion studies, funnel plots were found to be an inaccurate method of assessing publication bias. Journal of clinical epidemiology, 67(8), 897–903. doi: https://doi.org/10.1016/j.jclinepi.2014.03.003
Hunter, J., & Schmidt, F. (2000). Fixed effects vs. random effects meta-analysis models: Implications for cumulative research knowledge. International Journal of selection and assessment, 8(4), 275–292. doi: https://doi.org/10.1111/1468-2389.00156
Ioannidis, J. P., Patsopoulos, N. A., & Evangelou, E. (2007). Uncertainty in heterogeneity estimates in meta-analyses. British Medical Journal, 335(7626), 914–916. doi: https://doi.org/10.1136/bmj.39343.408449.80
Keithlin, J., Sargeant, J., Thomas, M. K., & Fazil, A. (2014). Systematic review and meta-analysis of the proportion of campylobacter cases that develop chronic sequelae. BMC Public Health, 14(1), 1–19. doi: https://doi.org/10.1186/1471-2458-14-1203
Knapp, G., Biggerstaff, B. J., & Hartung, J. (2006). Assessing the amount of heterogeneity in random-effects meta-analysis. Biometrical journal, 48(2), 271–285. doi: https://doi.org/10.1002/bimj.200510175
Lewis, S., & Clarke, M. (2001). Forest plots: trying to see the wood and the trees. British Medical Journal, 322(7300), 1479–1480. doi: https://doi.org/10.1136/bmj.322.7300.1479
Lijmer, J. G., Bossuyt, P. M., & Heisterkamp, S. H. (2002). Exploring sources of heterogeneity in systematic reviews of diagnostic tests. Statistics in medicine, 21(11), 1525–1537. doi: https://doi.org/10.1002/sim.1185
Lin, L., & Xu, C. (2020). Arcsine-based transformations for meta-analysis of proportions: Pros, cons, and alternatives. Health Science Reports, 3(3), e178. doi: https://doi.org/10.1002/hsr2.178
Lipsey, M. W., & Wilson, D. B. (2001). Practical meta-analysis. Sage Publications.
Littell, J. H., Corcoran, J., & Pillai, V. (2008). Systematic reviews and meta-analysis. Oxford University Press. doi: https://doi.org/10.1093/acprof:oso/9780195326543.001.0001
Ma, Y., Chu, H., & Mazumdar, M. (2016). Meta-analysis of proportions of rare events a comparison of exact likelihood methods with robust variance estimation. Communications in statistics: Simulation and computation, 45(8), 3036–3052.
MarksAnglin, A., & Chen, Y. (2020). A historical review of publication bias. Research synthesis methods, 11(6), 725–742. doi: https://doi.org/10.31222/osf.io/zmdpk
Maulik, P. K., Mascarenhas, M. N., Mathers, C. D., Dua, T., & Saxena, S. (2011). Prevalence of intellectual disability: a meta-analysis of population-based studies. Research in Developmental Disabilities, 32(2), 419–436. doi: https://doi.org/10.1016/j.ridd.2010.12.018
Miller, J. J. (1978). The inverse of the freeman-tukey double arcsine transformation. American Statistician, 32(4), 138. doi: https://doi.org/10.2307/2682942
Nyaga, V. N., Arbyn, M., & Aerts, M. (2014). Metaprop: a stata command to perform meta-analysis of binomial data. Archives of Public Health, 72(1), 39. doi: https://doi.org/10.1186/2049-3258-72-39
Petrie, A., Bulman, J. S., & Osborn, J. F. (2003). Further statistics in dentistry part 8: Systematic reviews and meta-analyses. British Dental Journal, 194(2), 73–78. doi: https://doi.org/10.1038/sj.bdj.4809877
Preston, C., Ashby, D., & Smyth, R. (2004). Adjusting for publication bias: modelling the selection process. Journal of Evaluation in Clinical Practice, 10(2), 313–322. doi: https://doi.org/10.1111/j.1365-2753.2003.00457.x
R Core Team. (2022). R: A language and environment for statistical computing [Computer software manual]. Vienna, Austria. Retrieved from http://www.R-project.org
Raudenbush, S. W., & Bryk, A. S. (1985). Empirical bayes meta-analysis. Journal of Educational Statistics, 10(2), 75–98. doi: https://doi.org/10.2307/1164836
Ried, K. (2006). Interpreting and understanding meta-analysis graphs: a practical guide. Australian Family Physician, 35(8), 635–638.
RStudio Team. (2022). Rstudio: Integrated development for R [Computer software manual]. Boston, MA. Retrieved from http://www.rstudio.com/
Rücker, G., Schwarzer, G., Carpenter, J. R., & Schumacher, M. (2008). Undue reliance on \({I}^2\) in assessing heterogeneity may mislead. BMC medical research methodology, 8, 1–9. doi: https://doi.org/10.1186/1471-2288-8-79
Sahai, H., & Ageel, M. I. (2012). The analysis of variance: Fixed, random and mixed models. Springer Science Business Media.
Schmidt, F. L., & Hunter, J. E. (2014). Methods of meta-analysis: Correcting error and bias in research findings. Sage Publications. doi: https://doi.org/10.4135/9781483398105
Schoonjans, F. (2017). Medcalc manual: Easy-to-use statistical software [Computer software manual]. Retrieved from https://www.medcalc.org/download/medcalcmanual.pdf
Schwarzer, G., Carpenter, J. R., & Rücker, G. (2015). Meta-analysis with R. Springer. doi: https://doi.org/10.1007/978-3-319-21416-0
Schwarzer, G., Chemaitelly, H., Abu-Raddad, L. J., & Rücker, G. (2019). Seriously misleading results using inverse of freeman-tukey double arcsine transformation in meta-analysis of single proportions. Research synthesis methods, 10(3), 476–483. doi: https://doi.org/10.1002/jrsm.1348
Song, F., Eastwood, A., Gilbody, S., Duley, L., & Sutton, A. (2000). Publication and related biases: a review. Health Technology Assessment, 4(10), 1–115.
Sterne, J. A., Gavaghan, D., & Egger, M. (2000). Publication and related bias in meta-analysis: power of statistical tests and prevalence in the literature. Journal of Clinical Epidemiology, 53(11), 1119–1129.
Tabachnick, B. G., Fidell, L. S., & Osterlind, S. J. (2013). Using multivariate statistics. Pearson.
Thompson, S. G. (1994). Why sources of heterogeneity in meta-analysis should be investigated. British Medical Journal, 309(6965), 1351–1355.
Thompson, S. G., & Higgins, J. P. (2002). How should meta-regression analyses be undertaken and interpreted? Statistics in Medicine, 21(11), 1539–1558. doi: https://doi.org/10.1002/sim.1187
Thompson, S. G., & Sharp, S. J. (1999). Explaining heterogeneity in meta-analysis: a comparison of methods. Statistics in Medicine, 18(20), 2693–2708. doi: 3.0.co;2-v" >https://doi.org/10.1002/(sici)1097-0258(19991030)18:20¡2693::aid-sim235¿3.0.co;2-v
Thorlund, K., Wetterslev, J., Awad, T., Thabane, L., & Gluud, C. (2011). Comparison of statistical inferences from the dersimonian-laird and alternative random-effects model meta-analyses-an empirical assessment of 920 cochrane primary outcome meta-analyses. Research Synthesis Methods, 2(4), 238–253.
Veroniki, A. A., Jackson, D., Viechtbauer, W., Bender, R., Bowden, J., Knapp, G., & Salanti, G. (2016). Methods to estimate the between-study variance and its uncertainty in meta-analysis. Research Synthesis Methods, 7(1), 55–79.
Vevea, J. L., & Hedges, L. V. (1995). A general linear model for estimating effect size in the presence of publication bias. Psychometrika, 60(3), 419–435. doi: https://doi.org/10.1007/bf02294384
Vevea, J. L., & Woods, C. M. (2005). Publication bias in research synthesis: sensitivity analysis using a priori weight functions. Psychological Methods, 10(4), 428–443. doi: https://doi.org/10.1037/1082-989x.10.4.428
Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48.
Viechtbauer, W., & Cheung, M. W. (2010). Outlier and influence diagnostics for meta-analysis. Research Synthesis Methods, 1(2), 112–125. doi: https://doi.org/10.1002/jrsm.11
Wang, K. S., & Liu, X. (2016). Statistical methods in the meta-analysis of prevalence of human diseases. Journal of Biostatistics and Epidemiology, 2(1), 20–24.
Wu, X., Long, E., Lin, H., & Liu, Y. (2016). Prevalence and epidemiological characteristics of congenital cataract: a systematic review and meta-analysis. Scientific Reports, 6(1), 1–10. doi: https://doi.org/10.1038/srep28564
Xu, C., et al. (2021). The Freeman–Tukey double arcsine transformation for the meta-analysis of proportions: Recent criticisms were seriously misleading. Journal of evidence-based medicine, 14(4), 259–261. doi: https://doi.org/10.1111/jebm.12445