Keywords: Bayesian analysis · Compositional data · Lasso · Spike and Slab Lasso.
Compositional data, also referred to as ipsative data or fractional data, are non-negative components that represent fractions of a finite whole. Examples include percentages that sum to 100, hours in a day that sum to 24, expenses on different items that sum to the total budget, etc. Since compositional data contain relative information within the whole, analyzing such data is valuable to better differentiate ratings and diminish response biases. Compositional data analysis can be employed whether all components contributing to the total have been quantified, or merely a subset of them (Chastin, Palarea-Albaladejo, Dontje, & Skelton, 2015). Although compositional data appear in many fields, including but not limited to geology, biology, economics, medicine, and psychology, the analysis of this type of data as predictors has received relatively little attention due to the unique challenge caused by the constant-sum constraint in compositional data, notably a statistical issue known as “exact collinearity”. With the collinearity issue, traditional statistical methods may yield biased parameter estimates, inflated standard errors, and reduced statistical power (e.g., Belsley, Kuh, & Welsch, 1980).
A common strategy to address the exact collinearity problem of compositional data is to use transformations. Since compositional data reside in a simplex and mainly carry relative information, a log-ratio transformation is typically employed, based on the Aitchison geometry (Aitchison, 1986). Suitable log-ratio representations include the additive-log-ratio (alr) transformation, the centered log-ratio (clr) transformation, and the isometric-log-ratio (ilr) transformation (Aitchison, 1986; Egozcue, Pawlowsky-Glahn, Mateu-Figueras, & Barceló-Vidal, 2003). However, the application of transformation-based methods for compositional data analysis presents certain drawbacks. First, transforming data containing zero values poses a challenge since log zero is undefined. To circumvent the singularity, it is typical to replace zero values with a small predetermined value. This approach, however, can introduce undesired bias and potentially produce misleading results, particularly when dealing with highly sparse data containing a substantial number of zeros (Aitchison & Bacon-Shone, 1984; Palarea-Albaladejo & Martin-Fernandez, 2013). Second, methods based on transformations struggle to provide clear interpretations, given their inability to fully disentangle the dependency among predictors. This means that a shift in a single predictor value inherently triggers alterations in other predictor values. As a result, it can distort the original data structure, thereby complicating the interpretation of the transformed data.
Because of the limitations of the transformation techniques, researchers have been seeking alternative strategies to handle compositional data and yield interpretable model estimation results (e.g., G. Li, Li, & Chen, 2023). It is shown in the literature that Bayesian methods are promising as even with exact collinearity, posteriors of the model parameters are well-defined. Although Bayesian compositional data analysis is sensitive to priors of the parameters, our previous findings demonstrated that Bayesian Lasso and Bayesian Spike-and-Slab Lasso (SSL) provide reasonable estimation results.
In this tutorial, we focus on linear regression and offer a hands-on exploration of both the Bayesian Lasso and Bayesian SSL methods to handle compositional predictors. By integrating Bayesian methods within the Lasso and SSL frameworks, we highlight the flexibility and robustness of our approach, thus enhancing the accuracy of parameter estimation and facilitating a more comprehensive understanding of the relationships among the compositional predictors and the outcome. The readers will learn how to implement the Bayesian Lasso and Bayesian SSL techniques using R (R Core Team, 2023), equipped with the Just Another Gibbs Sampler (JAGS) program (Plummer, 2003). The structure of the tutorial is organized as follows. We begin with a preliminaries section that provides a detailed introduction to compositional data, highlighting its complexities and challenges. We also explore penalized methods, focusing specifically on the Lasso and SSL techniques. This leads to a section dedicated to Bayesian methods, where we establish the theoretical basis for the Bayesian Lasso and Bayesian SSL methodologies. The subsequent sections demonstrate the implementation of these Bayesian methods in JAGS. We conclude the tutorial with a summary of insights and implications drawn from our discussion.
This tutorial focuses on a linear regression model with compositional predictors, given by:
\begin {equation} y_{i}=\beta _{0}+\mathbf {x}_{i}^{T}\boldsymbol {\beta }+\varepsilon _{i},\quad \varepsilon _{i}\sim \mathcal {N}\left (0,\sigma ^{2}\right ),\label {eq:Reg} \end {equation} where \(y_{i}\) represents the outcome for the \(i\)th subject (\(i=1,\ldots ,n\), \(n\) is the total sample size), \(\beta _{0}\) is the intercept, \(\mathbf {x}_{i}=(x_{i1},\ldots ,x_{ip})^{T}\) is a vector of compositional predictors with \(p\) components for the \(i\)th subject, \(\boldsymbol {\beta }=\left (\beta _{1},\ldots ,\beta _{p}\right )^{T}\) represents a \(p\)-dimensional vector of unknown regression coefficients, and \(\varepsilon _{i}\) is the random error following a normal distribution with mean 0 and unknown variance \(\sigma ^{2}\). According to the definition, compositional data with \(p\) components refers to non-negative numbers whose sum is a constant. Namely, \(x_{i1}>0,\ldots ,x_{ip}>0\), and \begin {equation} \sum _{j=1}^{p}x_{ij}=c,\label {eq:Compositional data} \end {equation} where \(c\) is a constant. Without loss of generality, we set \(c\) at 1. Under the sum-to-one constraint, the following issues may arise:
(1) The components of compositional data fall within the \((0,1)\) interval, which can complicate the prediction of the dependent variable due to the limited range of possible outcomes.
(2) The sum-to-one constraint leads to an exact collinearity problem among predictors, which poses a significant challenge to standard regression techniques, as they typically operate under the assumption of predictor independence.
(3) Real-world compositional data frequently manifest a high degree of sparsity, i.e., a large share of the components could be zero. This introduces additional intricacies to the analysis, as discerning whether a zero value signifies a genuine absence of the component or merely results from measurement limitations can be challenging.
In this tutorial, our focus lies on scenarios typified where a proportion of \(\boldsymbol {\beta }\) are either zero or sufficiently small to render the majority of potential predictors insignificant in the analysis. Within this framework, we have two main goals: (i) discerning the influential predictors, and (ii) precisely estimating the magnitude of their corresponding effects.
To address collinearity, frequentist approaches often use a penalized likelihood to obtain sparse estimates of the regression coefficient. These methods involve adding a penalty term into the model to regulate the magnitude of the coefficients and effectively shrinking them towards zero to reduce their variance. Similar to ordinary least squares (OLS) estimation, penalized regression methods estimate the regression coefficients \(\beta \) by minimizing the penalized residual sum of squares, given by:
\begin {equation} \min _{\beta }\left \{ \sum _{i=1}^{n}\left (y_{i}-\beta _{0}-\mathbf {x}_{i}^{T}\boldsymbol {\beta }\right )^{2}+\operatorname {pen}_{\lambda }(\boldsymbol {\beta })\right \} .\label {eq:Penalized least squares regression} \end {equation} The penalized term \(\operatorname {pen}_{\lambda }(\boldsymbol {\beta })\) can maintain all features while diminishing the coefficients’ magnitude in the model. A widely used approach is the Least Absolute Shrinkage and Selection Operator (Lasso), introduced by Tibshirani (1996), which incorporates an \(L1\) penalty term into the objective function, expressed as \(\operatorname {pen}_{\lambda }(\boldsymbol {\beta })=\lambda \sum _{j=1}^{p}|\beta _{j}|\) . The parameter \(\lambda \) can be tuned to set the shrinkage level: the higher the \(\lambda \) is, the more coefficients are shrunk to zero. This approach aims to enhance predictive precision and identify a concise group of significant predictors.
However, in high-dimensional scenarios, traditional Lasso may arbitrarily select only one predictor from a group of highly correlated variables, potentially leading to biased estimations and reduced interpretability (Zou & Hastie, 2005). Additionally, Lasso employs a constant penalty for all coefficients and could unintentionally result in the inclusion of irrelevant predictors (Friedman, Hastie, & Tibshirani, 2010). These issues are particularly pertinent in compositional data analysis, where each predictor represents a fraction of the total. The presence of irrelevant predictors can skew these fractions, potentially leading to inaccurate interpretations (W. Lin, Shi, Feng, & Li, 2014).
To reduce the bias of Lasso, Ročkov’a and George (2018) introduced the Spike-and-Slab Lasso (SSL), an advanced technique that incorporates penalized likelihood in the Bayesian framework. The SSL methodology has become a prevalent tool for handling diverse statistical problems due to its inherent flexibility and versatility. For example, Tang, Shen, Zhang, and Yi (2017b) and Tang et al. (2018) used SSL within the framework of generalized linear models to enhance the accuracy of disease outcome prediction and improve gene detection efficiency. In the context of multivariate regression, Deshpande, Ročková, and George (2019) developed a multivariate SSL to offer an effective solution for simultaneous predictor selection and effect estimation. Moreover, Z. Li, McCormick, and Clark (2019) proposed an innovative class of priors for Bayesian inference using SSL in multiple Gaussian graphical models, demonstrating its ability to facilitate simultaneous self-adaptive shrinkage and model selection. Also, the integration of SSL into Cox proportional hazards models by Tang, Shen, Zhang, and Yi (2017a) has significantly advanced survival data analysis by offering a nuanced understanding of time-dependent risks.
In general, penalized least squares methods are often effective for identifying important predictors and managing collinearity in regression analysis. However, when applied to compositional data, these methods in the frequentist framework still require a transformation of compositional predictors, which struggle to provide straightforward interpretations. To address this, we propose a shift towards a Bayesian framework. This shift is grounded in the equivalence between the frequentist penalized regression approach and the Bayesian approach, where a normal likelihood combined with specific priors leads to a posterior distribution akin to the penalized likelihood. In our Bayesian framework, we integrate Lasso and SSL priors, enhancing the interpretability of results with compositional data. We introduce Bayesian Lasso and Bayesian SSL below.
Tibshirani (1996) suggested that Lasso estimates can be interpreted as posterior modes when regression coefficients have independent and identically distributed Laplace (double-exponential) priors. Thus, the prior for the regression coefficients \(\boldsymbol {\beta }\) given the error variance \(\sigma ^{2}\) with hyperparameter \(\lambda \) is defined as
\begin {equation} p\left (\boldsymbol {\beta }\mid \sigma ^{2}\right )=\prod _{j=1}^{p}\frac {\lambda }{2\sqrt {\sigma ^{2}}}\exp \left \{ \frac {-\lambda \left |\beta _{j}\right |}{\sqrt {\sigma ^{2}}}\right \} .\label {eq:Bayesian Lasso} \end {equation} Park and Casella (2008) pointed out that this Laplace distribution is equivalent to a continuous mixture of Gaussian distributions (Andrews & Mallows, 1974). Specifically, the expression for the Laplace distribution as a scale mixture of normals (with an exponential mixing density) is given by
\begin {equation} \begin {aligned}\frac {\lambda }{2}\exp (-\lambda |\beta |)= & \int _{0}^{\infty }\frac {1}{\sqrt {2\pi \tau ^{2}}}\exp \left (-\beta ^{2}/2\tau ^{2}\right )\times \frac {\lambda ^{2}}{2}\exp \left (-\frac {\lambda ^{2}\tau ^{2}}{2}\right )\mathrm {d}\tau ^{2}\end {aligned} ,\label {eq:Laplace distribution} \end {equation} where \(\tau ^{2}\) serves as a scaling factor. This suggests the following hierarchical representation of the full model:
\begin {equation} \begin {gathered}{y_{i}\mid \beta _{0},\mathbf {x}_{i},\boldsymbol {\beta },\sigma ^{2}\sim \mathcal {N}\left (\beta _{0}+\mathbf {x}_{i}^{T}\boldsymbol {\beta },\sigma ^{2}\right )},\\ \boldsymbol {\beta }\mid \sigma ^{2},\tau _{1}^{2},\ldots ,\tau _{p}^{2}\sim \mathcal {N}\left (\mathbf {0},\sigma ^{2}\boldsymbol {D}_{\tau }\right ),\\ \beta _{0}\sim \mathcal {N}\left (0,100\right )\\ \sigma ^{2},\tau _{1}^{2},\ldots ,\tau _{p}^{2}\sim p\left (\sigma ^{2}\right )\prod _{j=1}^{p}\frac {\lambda ^{2}}{2}\exp \left \{ \frac {-\lambda ^{2}\tau _{j}^{2}}{2}\right \} . \end {gathered} \label {eq:Hierarchical posterior} \end {equation} In this model, \(\boldsymbol {D}_{\tau }\) is a diagonal matrix with diagonal elements \(\tau _{1}^{2},\ldots ,\tau _{p}^{2}\). The exponential distribution for \(\tau _{j}^{2}\) reflects the Lasso penalty, with \(\lambda \) controlling the amount of penalization. For \(\sigma ^{2}\), we choose a non-informative scale-variant prior, such as \(p\left (\sigma ^{2}\right )=1/\sigma ^{2}\). Or, to ensure model conjugacy, an inverse-gamma prior for \(\sigma ^{2}\) can be utilized.
In contrast to traditional Lasso that necessitates manual adjustment of its penalty hyperparameter, the Bayesian Lasso facilitates the empirical estimation of the shrinkage degree. This capability significantly improves the model’s effectiveness in handling complexity and mitigating issues of collinearity. However, despite these benefits, Ročková and George (2016) identified certain shortcomings in the Bayesian Lasso, particularly its limited capacity to accommodate sparsity and to rectify estimation bias. Further, as Ghosh, Tang, Ghosh, and Chakrabarti (2013) indicates, it tends to insufficiently shrink less significant coefficients while excessively shrinking more important ones. The following subsection will explore how the Bayesian SSL addresses these specific challenges.
Unlike Lasso, which imposes uniform shrinkage across all regression coefficients \(\boldsymbol {\beta }\), the SSL employs a mixture prior structure. Each coefficient \(\beta _{j}\) comes from either a Laplacian "spike" centered around zero or a broader Laplacian "slab". The hierarchical prior over \(\boldsymbol {\beta }\) and the latent indicator variables \(\boldsymbol {\gamma }=\left (\gamma _{1},\ldots ,\gamma _{p}\right )\) is given by: \begin {equation} \begin {aligned} & p(\boldsymbol {\beta }\mid \gamma )=\prod _{j=1}^{p}\left [\left (1-\gamma _{j}\right )\psi _{0}\left (\beta _{j}\right )+\gamma _{j}\psi _{1}\left (\beta _{j}\right )\right ],\quad \gamma \sim p(\boldsymbol {\gamma }),\end {aligned} \label {eq:spike and slab Lasso} \end {equation} where \(\gamma =\left (\gamma _{1},\ldots ,\gamma _{p}\right )^{\prime }\), with each \(\gamma _{i}\) being a binary variable, is an intermediate vector, indexing the \(2^{p}\) conceivable models within the framework. Here, \(\psi _{0}\left (\beta \right )=\left (\lambda _{0}/2\right )e^{-\left |\beta \right |\lambda _{0}}\) is the “spike” and \(\psi _{1}\left (\beta \right )=\left (\lambda _{1}/2\right )e^{-\left |\beta \right |\lambda _{1}}\) is the “slab” \(\left (\lambda _{1}\ll \lambda _{0}\right )\) . This two-point mixture of Laplace distributions will be referred to as the SSL priors. The flexibility of the model space prior \(p(\gamma )\) substantially broadens the scope of these priors. It allows for the tailoring of \(p(\beta )\) towards preferred configurations of \(\gamma \), enhancing the model’s ability to align with specific, desirable configurations. For our analysis, we focus on of the following form:
\begin {equation} p(\boldsymbol {\gamma }\mid \theta )=\prod _{j=1}^{p}\theta ^{\gamma _{j}}(1-\theta )^{1-\gamma _{j}},\quad \text { and }\quad \theta \sim \operatorname {Beta}(a,b), \end {equation} where \(\theta =\mathrm {P}\left (\gamma _{j}=1\mid \theta \right )\) represents the prior expected fraction of substantial \(\beta _{j}\). This hyperparameter \(\theta \) plays a pivotal role in the mixture prior, as it balances the influence of the spike and slab components by controlling the mixture probabilities for each coefficient \(\beta _{j}\). Additionally, \(a\) and \(b\) serve as hyperparameters in the Beta distribution, further shaping the overall behavior of the model.
In the Bayesian SSL framework, our sampling methodology for the Spike-and-Slab Lasso posterior relies on the Stochastic Search Variable Selection (SSVS) algorithm (George & McCulloch, 1993). This approach interprets the Laplace distribution as a scale mixture of Gaussians defined by penalty parameters \(\lambda _{j}>0\). The mixing distribution is exponential, with the rate parameter set at \(\lambda _{j}^{2}/2\), following the approach outlined in Park and Casella (2008). Thus, regression with SSL priors takes the following hierarchical form:
\begin {equation} \begin {aligned} & y_{i}\mid \beta _{0},\mathbf {x}_{i},\boldsymbol {\beta },\sigma ^{2}\sim \mathcal {N}\left (\beta _{0}+\mathbf {x}_{i}^{T}\boldsymbol {\beta },\sigma ^{2}\right ),\\ & \beta _{0}\sim \mathcal {N}\left (0,100\right ),\\ & \boldsymbol {\beta }\mid \boldsymbol {\tau }\sim \mathcal {N}\left (\mathbf {0},\sigma ^{2}\boldsymbol {D}_{\tau }\right ),\\ & {\tau _{j}^{2}\sim \operatorname {Exp}\left (\frac {\lambda _{j}^{2}}{2}\right ),}\\ & \lambda _{j}=\gamma _{j}\lambda _{1}+\left (1-\gamma _{j}\right )\lambda _{0},\\ & \gamma _{j}\mid \theta \sim \operatorname {Bernoulli}(\theta )\quad \text { with }\quad \theta \sim \operatorname {Beta}(a,b),\\ & {\sigma ^{2}\sim InvGamma(0.001,0.001)}\text {.} \end {aligned} \end {equation} In the model, \(\boldsymbol {D}_{\tau }\) represents a diagonal matrix, with its diagonal comprising the elements \(\tau _{1}^{2},\ldots ,\tau _{p}^{2}\). The hyperparameters \(\lambda _{1}\) and \(\lambda _{0}\) are used for computing \(\lambda _{j}\), and are typically chosen based on prior knowledge, with \(\lambda _{1}\) being considerably smaller than \(\lambda _{0}\) (expressed as \(\lambda _{1}\ll \lambda _{0}\) ). The model’s spike-and-slab component is encapsulated by the latent variables \(\gamma _{1},\ldots ,\gamma _{p}\), each adhering to a Bernoulli distribution characterized by the parameter \(\theta \), symbolized as \(\operatorname {Bernoulli}(\theta )\). Furthermore, the parameter \(\theta \) itself is modeled using a Beta distribution, determined by the shape parameters \(a\) and \(b\). Again for \(\sigma ^{2}\), we can choose a non-informative scale-variant prior, such as \(p\left (\sigma ^{2}\right )=1/\sigma ^{2}\). Or, to ensure model conjugacy, an inverse-gamma prior for \(\sigma ^{2}\) can be utilized.
The Bayesian SSL introduces a more sophisticated model for variable selection. It combines the shrinkage property of the Lasso with a spike-and-slab prior, allowing for a more flexible and nuanced approach. This hierarchical structure not only enhances the model’s flexibility but also aids in capturing the underlying complexities of the data. This methodology is particularly effective in dissecting the intricate structure of compositional data, offering a comprehensive understanding of the underlying relationships within the dataset.
Next, we delve into the practical implementation of the Bayesian Lasso and Bayesian SSL using the rjags package.
In this section, we introduce how to use the rjags package in the R environment (Plummer, 2003) to call JAGS and carry out Bayesian compositional analysis. JAGS, short for Just Another Gibbs Sampler, can be installed from the following link: https://mcmc-jags.sourceforge.io/.
The following chunk of code loads the necessary packages for our entire tutorial. If you haven’t installed these packages previously, you will need to install them first using install.packages(). In our Bayesian analysis, we utilize rjags for interfacing R with JAGS, while coda assists in summarizing MCMC outputs. These tools collectively streamline the implementation and evaluation of Bayesian models in R.
library(rjags) # rjags library allows R to interface with JAGS library(coda) # coda package provides tools for summarizing and visualizing MCMC output library(ggmcmc) # ggmcmc is used for diagnostics of MCMC chains and plots library(MASS) # MASS for generating multivariate normal data library(Matrix) # Matrix package is for matrix computations, particularly for sparse matrices library(MCMCpack) # Commonly used for generating samples from a Dirichlet distribution in R }
For illustration, we generate a compositional data matrix with \(n=50\) subjects and \(p=10\) components. Two commonly used compositional data generation methods are introduced below.
We start by generating a matrix X of random variables, following normal distributions. Each row of X represents observations from one subject, and each column represents a component. Then, compositional data can be obtained by dividing each element in X by its corresponding row sum. After the conversion, elements in each row sum to 1.
p <- 10 # Define the number of variables N <- 50 # Define the number of observations # Initialize a matrix Z with N rows and p columns to hold the generated normal data X <- matrix(rnorm(N * p), nrow = N, ncol = p) # Normalize each row so that they sum to 1 (compositional data) X <- X / rowSums(X)
Dirichlet distribution is a common choice for generating compositional data because it inherently produces a vector of values that sum to 1. It is a multivariate generalization of the beta distribution. Compositional predictors can be directly generated from a Dirichlet distribution as below.
p <- 10 # Define the number of variables N <- 50 # Define the number of observations alpha <- rep(1, p) # Specify hyperparameters for the Dirichlet distribution # Initialize an empty matrix X with N rows and p columns to hold the generated data X <- matrix(0, nrow = N, ncol = p) # Fill the matrix X with random values drawn from the Dirichlet distribution for (i in 1:N) { X[i,] <- rdirichlet(1, alpha) }
After compositional predictors are generated, we generate the outcomes based on Equation (1), with the intercept \(\beta _{0}=1\), coefficient values \(\boldsymbol {\beta }\) = \((-2,-1.5,-1,0,\) \(1,1.5,2,0,0,0)^{T}\) and error variance \(\sigma ^{2}=0.01\). A subset of the generated data is presented in Table 1.
q <- 6 # Define the number of non-zero regression coefficients # Define the true regression coefficients; first q coefficients are non-zero, rest are zero beta_scenario <- c(-2, -1.5, -1, 0, 1, 1.5, 2, rep(0, p - q-1)) # Generate the outcome variable y based on equation (1) y <- 1 + X %*% beta_scenario + rnorm(N, sd = 0.1)
| Y | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 |
| 1.169 | 0.065 | 0.105 | 0.036 | 0.040 | 0.110 | 0.214 | 0.025 | 0.007 | 0.260 | 0.138 |
| -0.040 | 0.428 | 0.065 | 0.098 | 0.204 | 0.052 | 0.031 | 0.005 | 0.001 | 0.015 | 0.101 |
| 0.162 | 0.507 | 0.002 | 0.047 | 0.106 | 0.032 | 0.035 | 0.074 | 0.001 | 0.181 | 0.015 |
| 0.650 | 0.296 | 0.024 | 0.013 | 0.019 | 0.019 | 0.067 | 0.166 | 0.218 | 0.106 | 0.071 |
| 0.185 | 0.313 | 0.300 | 0.045 | 0.055 | 0.097 | 0.093 | 0.003 | 0.032 | 0.042 | 0.377 |
For illustration purpose, we use one dataset generated using Method 2 to demonstrate the implementation of Bayesian Lasso below.
Step 1: Define JAGS model
In this step, we define a Bayesian Lasso regression model using JAGS. The model is specified in a string format and includes components for the likelihood, priors for the regression coefficients \(\beta \), and other model parameters.
model_string_Lasso <- " model { # Likelihood for (i in 1:N) { y[i] ~ dnorm(mu[i], pre_sig2) # normal distribution for y mu[i] <- beta0+sum(beta[] * X[i,]) # model for the mean } # Prior for beta0 (intercept) beta0 ~ dnorm(0, 1.0E-2) # Assuming a weakly informative prior # Prior for sigma2 pre_sig2 ~ dgamma(0.01,0.01) #gamma prior for precision sigma2 <- 1/pre_sig2 # Priors for beta coefficients for (j in 1:p) { # Using the scale mixture representation of the Laplace distribution: beta[j] ~ dnorm(0, tau_beta[j]) tau_beta[j] <- 1 / (sigma2 * tau_sq[j]) # Prior for tau_sq[j] (related to the Lasso penalty) tau_sq[j] ~ dexp(lambda^2 / 2) # follows an exponential distribution with rate lambda^2 / 2 } } "
Step 2: Specify initial values and prepare data
In this step, we define initial values for the parameters in the Bayesian Lasso regression model. It is recommended to use estimates from a standard least squares regression as initial values for the \(\lambda \) parameter in the Bayesian Lasso model.
In JAGS, users have the choice of using user-specified initial values or default values from random number generators (RNGs). Our explanations will cover both methods. For illustration, we let RNGs determine initial values for Bayesian Lasso and use user-defined initial values for Bayesian SSL.
The base module in JAGS includes four distinct Random Number Generators (RNGs), each identified by the following names: “base::Wichmann-Hill”, “base::Marsaglia-Multicarry”, “base::Super-Duper”, and “base::Mersenne-Twister”. To initialize the RNG of your choice, simply specify its name along with a seed value (for example, a seed of 111), as illustrated in the subsequent code example:
# Initial values for the parameters # Automatically generated initial values inits_lasso <- list(".RNG.name"="base::Wichmann-Hill", ".RNG.seed"=111)
We then prepare the data in a list format to be compiled with the model in JAGS.
# Data preparation # N: the number of observations. # p: the number of predictors. # X: the design matrix. # y: the response variable (converted to a vector using as.vector(y)). lambda <- p * sqrt(var(lm(y ~ X- 1)$residuals)) / sum(abs(lm(y ~ X- 1)$coefficients)) data_lasso <- list(N = N, p = p, X= X, y = as.vector(y), lambda = lambda)
Step 3: Fit the model via JAGS
In our Bayesian Lasso model, we use a Markov chain Monte Carlo (MCMC) algorithm. Note that the number of chains is set at 1 (n.chains = 1) for simplicity, but it can be easily set at a larger value to check between-chains convergence, which is crucial for a reliable model. We run the MCMC for 5000 iterations (update(fit, 5000)) as a burn-in period, and then use 20,000 more iterations (n.iter = 20000) to get a detailed view of the parameters.
fit <- jags.model( textConnection(model_string_Lasso), # Model specification. data = data_lasso, # The data. inits=inits_lasso, # The initial values for the model parameters. n.chains = 1, # The number of Markov chains. n.adapt = 1000 # The number of adaptation iterations ) params <- c("beta0","beta","sigma2") update(fit, 5000) # burn-in samples <- coda.samples(fit, variable.names = params, n.iter = 20000) #save results into model.res model.res <- as.mcmc(do.call(rbind,samples))
Step 4: Convergence diagnostic via traceplots and Geweke tests
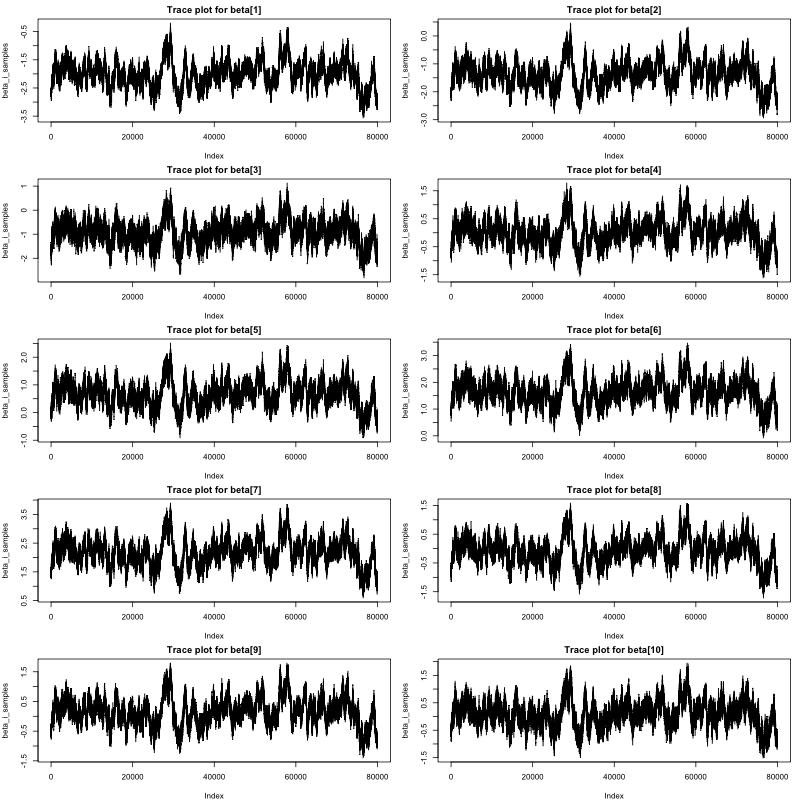
Prior to examining the results of parameter estimates, we assess the convergence of the Markov chains using two common diagnostic tools: traceplots and Geweke tests.
The traceplots of the Markov chains for \(\boldsymbol {\beta }\) are displayed in Figure1. Clearly, all chains converged, indicating effective sampling from the posterior distributions for all coefficients \(\beta _{1}\) through \(\beta _{10}\). Geweke test results are given below. With Geweke statistics falling between the -1.96 to 1.96 range, there is no evidence against convergence, suggesting that the model estimation is reliable for interpretation.
# Trace plot race_plot <- traceplot(samples) # geweke tests geweke.diag(model.res) Fraction in 1st window = 0.1 Fraction in 2nd window = 0.5 beta[1] beta[2] beta[3] beta[4] -0.14747 -0.06480 -0.08991 -0.02971 beta[5] beta[6] beta[7] beta[8] -0.16094 0.14410 -0.16851 -0.06328 beta[9] beta[10] -0.16662 -0.04245

Step 5: Plot regression coefficients estimation for interpretation
In this step, we focus on visualizing the estimates of the beta coefficients for better interpretation and understanding.
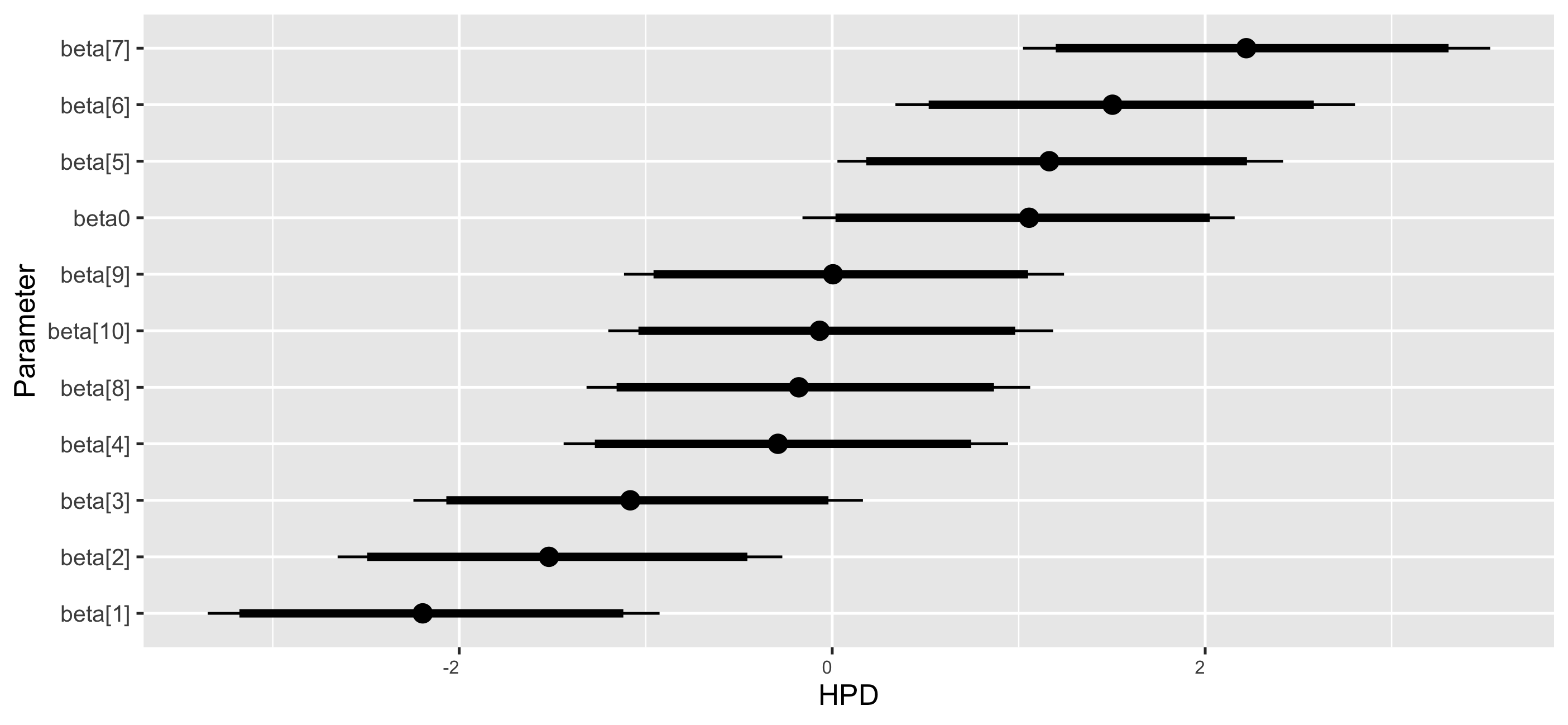
# Convert the results from JAGS into a format that ’ggmcmc’ can use. ggmcmc_object <- ggs(model.res) # Creates a caterpillar plot which is used for visualizing the posterior distributions of the parameters. ggs_caterpillar(D = ggmcmc_object, family = "beta")
The coefficient dot plots of the Markov chains for \(\beta \) are in Figure 2. The black points represent the mean estimates of the coefficients. The black lines indicate the range of these estimates, extending from the 2.5% percentile to the 97.5% percentile. Specifically, the coefficients \(\beta _{1}\), \(\beta _{2}\), and \(\beta _{3}\) are notably negative, with their 95% credible intervals excluding zero. This indicates a substantial negative influence on the outcome variable as the corresponding predictor proportions increase. Coefficients \(\beta _{5}\), \(\beta _{6}\), and \(\beta _{7}\) are positive, with credible intervals also excluding zero, suggesting a significant positive effect on the outcome variable with increasing proportions of these predictors. The coefficient \(\beta _{4}\), \(\beta _{8}\), \(\beta _{9}\), and \(\beta _{10}\) are close to zero with credible intervals that encompass zero, indicating no discernible impact on the outcome variable.
Step 6: Summarize posterior MCMC samples
In this step, we summarize the model estimation results from the MCMC procedure conducted in JAGS. The summary() function provides a comprehensive overview of the posterior distributions for each parameter in the model. From the results, the model appears to perform well in estimating the true values of the regression coefficients. The empirical means are close to the true values, and the true values generally fall within the 95% credible intervals of the estimates. Due to sampling errors of one set of simulated data, there is bias. But the small bias (-0.18, -0.01, -0.07, -0.29, 0.17, 0.01, 0.22, -0.17, 0.01, -0.06) for the coefficients \(\boldsymbol {\beta }\) demonstrates the effectiveness of Bayesian Lasso in capturing the underlying true values of the coefficients.
summary(samples) Iterations = 6001:26000 Thinning interval = 1 Number of chains = 1 Sample size per chain = 20000 1. Empirical mean and standard deviation for each variable, plus standard error of the mean: Mean SD Naive SE Time-series SE beta[1] -2.18754 0.5981 0.002115 0.07902 beta[2] -1.51041 0.5877 0.002078 0.07892 beta[3] -1.07185 0.6009 0.002124 0.07484 beta[4] -0.29220 0.5845 0.002067 0.07816 beta[5] 1.17219 0.5913 0.002090 0.08011 beta[6] 1.51421 0.6062 0.002143 0.07398 beta[7] 2.22883 0.6215 0.002197 0.07185 beta[8] -0.17333 0.5853 0.002069 0.08046 beta[9] 0.01159 0.5794 0.002048 0.07991 beta[10] -0.06262 0.5853 0.002069 0.07988 beta0 1.05053 0.5703 0.002016 0.08483 2. Quantiles for each variable: 2.5% 25% 50% 75% 97.5% beta[1] -3.34861 -2.5699 -2.196116 -1.83954 -0.9258 beta[2] -2.65227 -1.8809 -1.519331 -1.17487 -0.2676 beta[3] -2.24595 -1.4559 -1.082853 -0.70673 0.1647 beta[4] -1.44032 -0.6641 -0.291097 0.04308 0.9430 beta[5] 0.02786 0.7949 1.163895 1.51551 2.4180 beta[6] 0.33887 1.1301 1.502785 1.86480 2.8035 beta[7] 1.02289 1.8299 2.220343 2.60242 3.5282 beta[8] -1.31749 -0.5395 -0.179262 0.15835 1.0615 beta[9] -1.11653 -0.3470 0.003906 0.33893 1.2432 beta[10] -1.20086 -0.4322 -0.067443 0.26883 1.1846 beta0 -0.15954 0.7427 1.055721 1.40493 2.1579
Step 1: Define JAGS model
In this step, we define a Bayesian SSL regression using JAGS syntax. The model is specified in a string format and includes components for the likelihood, priors for the regression coefficients, and other model parameters.
model_string_SSL <- " model { # ----------------- # Likelihood # ----------------- for (i in 1:N) { y[i] ~ dnorm(mu[i], pre_sig2) mu[i] <- beta0 + sum(beta[] * X[i,]) } # Priors for beta and reparameterization for Laplace prior for (i in 1:p) { # Prior for gamma (Bernoulli distribution) gamma[i] ~ dbern(theta) # Binary variable following Bernoulli distribution. # Definition of lambda lambda[i] <- gamma[i] * lambda1 + (1 - gamma[i]) * lambda0 #Mixing two lambda values based on gamma # Prior for beta (Normal distribution with mean 0 and precision tau) tau_sq[i] ~ dexp(lambda[i]^2 / 2) beta[i] ~ dnorm(0, tau_beta[i]) tau_beta[i] <- 1 / (sigma2 * tau_sq[i]) } theta ~ dbeta(a, b) # Beta prior for theta (Bernoulli parameter) beta0 ~ dnorm(0, 0.01) # Normal prior for the intercept pre_sig2 ~ dgamma(0.01,0.01) # Precision follows a gamma distribution sigma2 <- 1/pre_sig2 # Definition of sigma squared (variance) as the reciprocal of precision } "
Step 2: Specify initial values and prepare data
Here, in the Bayesian SSL approach for illustration, we set initial values for model parameters using user-specified initial values.
# Initial values # Define Initial Values inits <- list(list(gamma = rep(1, p), beta0 = rnorm(1, 0, 1), pre_sig2 = 1 , theta = 0.5, beta = rep(0, p) )) # Prepare data list data_list_SSL <- list( y = as.vector(y), # Response variable X = X, # Matrix of predictors N = N, # Number of observations p = p, # Number of predictors a = 2, # Hyperparameter for the Beta distribution prior on theta b = p, # Hyperparameter for the Beta distribution prior on theta lambda1 = 0.1, # Hyperparameter for the lambda calculation lambda0 = 4 # Hyperparameter for the lambda calculation )
Step 3: Fit the Bayesian SSL model via JAGS
The code below serves to run the model and manage the adaptation and burn-in phases of the MCMC procedure.
fit <- jags.model( textConnection(model_string_SSL), # Model specification. data = data_list_SSL, # The data. inits = inits_SSL, # The initial values for the model parameters. n.chains = 1, # The number of Markov chains. n.adapt = 1000 # The number of adaptation iterations ) update(fit, 2000) params <- c("beta","beta0","sigma2") #run 30000 iterations after the burn-in priord samples <- coda.samples(fit, params, n.iter = 30000) #save results into model.res model.res <- as.mcmc(do.call(rbind,samples))
Step 4: Convergence diagnostic via traceplots and Geweke tests
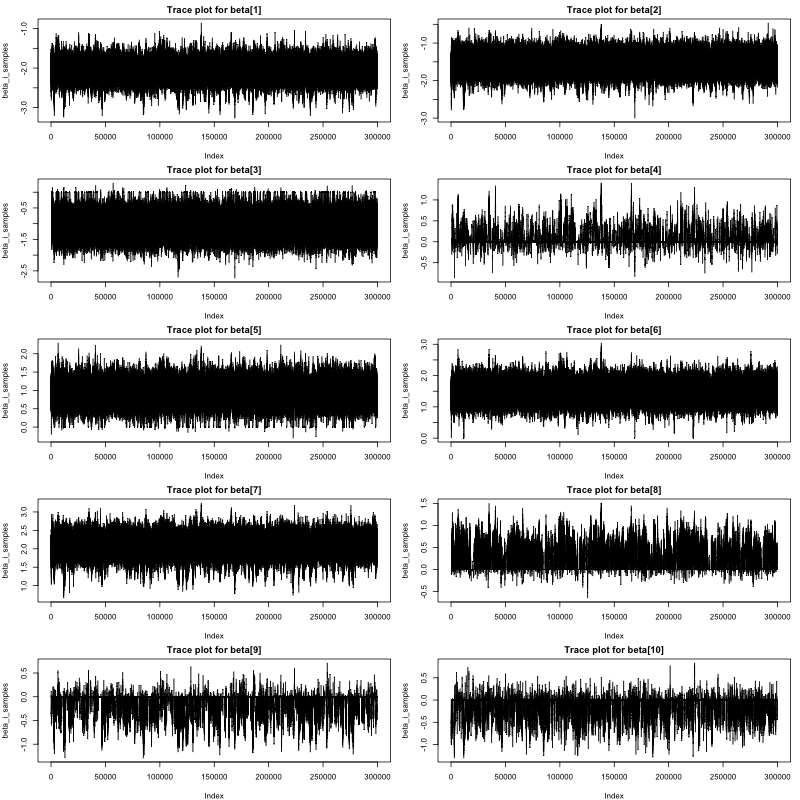
The model convergence is again assessed using two common diagnostic tools: traceplots and Geweke tests.
# Trace plot race_plot <- traceplot(samples) # geweke tests geweke.diag(model.res) Fraction in 1st window = 0.1 Fraction in 2nd window = 0.5 beta[1] beta[2] beta[3] beta[4] beta[5] beta[6] beta[7] beta[8] -0.2644 -0.2936 -0.3114 -0.3153 -0.4079 -0.2915 -0.3601 -0.5842 beta[9] beta[10] beta0 -0.3861 -0.6112 0.3281
The traceplots of the Markov chains for \(\boldsymbol {\beta }\) using Bayesian SSL are given in Figure 3. Again, both traceplots and Geweke tests imply that all Markov chains converged, thus parameter estimates can be trusted.
Step 5: Plot regression coefficients estimation for interpretation
In this step, we focus on visualizing the estimates of the beta coefficients from our Bayesian model for better interpretation and understanding.
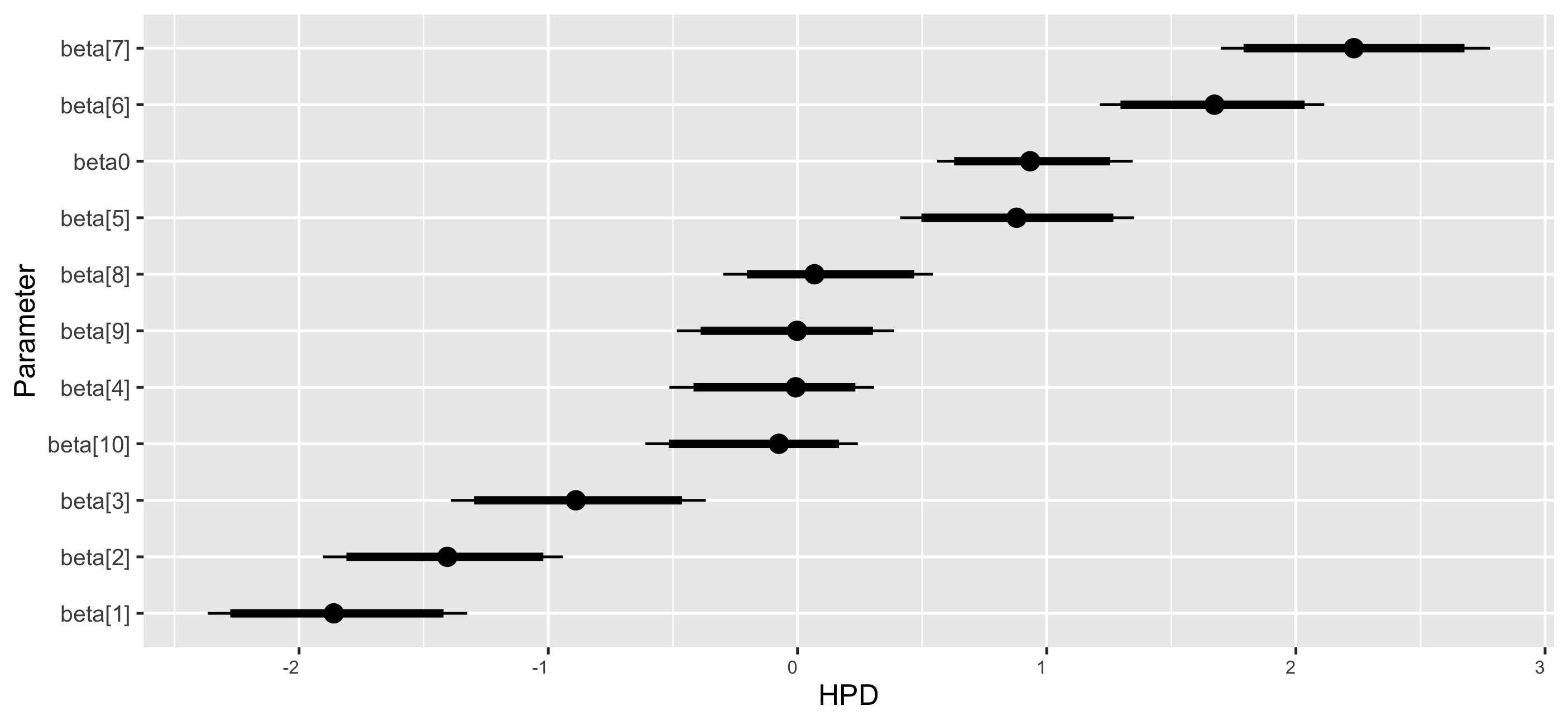
# Convert the results from JAGS into a format that ’ggmcmc’ can use. ggmcmc_object <- ggs(model.res) # Creates a caterpillar plot which is used for visualizing the posterior distributions of the parameters. ggs_caterpillar(D = ggmcmc_object, family = "beta")
The coefficient dot plots of the Markov chains for \(\boldsymbol {\beta }\) are provided in Figure 4. The posterior estimates for the regression coefficients are depicted in the plot. The interpretation from the Bayesian SSL model is the same as that from the Bayesian Lasso model.
Step 6: Summarize posterior MCMC samples
In this step, we summarize the model estimation results. The parameter estimates from Bayesian SSL are similar to those from the Bayesian Lasso model. Thus, the detailed interpretations are omitted here.
summary(samples) Iterations = 3001:33000 Thinning interval = 1 Number of chains = 1 Sample size per chain = 30000 1. Empirical mean and standard deviation for each variable, plus standard error of the mean: Mean SD Naive SE Time-series SE beta[1] -1.879920 0.23686 0.0013675 0.0050494 beta[2] -1.164649 0.17559 0.0010138 0.0031632 beta[3] -0.806203 0.18310 0.0010571 0.0033090 beta[4] -0.008885 0.05826 0.0003363 0.0017450 beta[5] 1.091903 0.15091 0.0008713 0.0036028 beta[6] 1.582677 0.14494 0.0008368 0.0017249 beta[7] 2.005218 0.17140 0.0009896 0.0035410 beta[8] 0.006645 0.04939 0.0002851 0.0012593 beta[9] -0.001426 0.03078 0.0001777 0.0002378 beta[10] 0.001519 0.03137 0.0001811 0.0002364 beta0 0.933072 0.06327 0.0003653 0.0020230 2. Quantiles for each variable: 2.5% 25% 50% 75% 97.5% beta[1] -2.33530 -2.03941 -1.8821989 -1.72026 -1.41082 beta[2] -1.50748 -1.28124 -1.1653645 -1.04836 -0.81613 beta[3] -1.16813 -0.92793 -0.8068750 -0.68623 -0.44117 beta[4] -0.15571 -0.02149 -0.0022969 0.01305 0.07433 beta[5] 0.79652 0.99090 1.0918781 1.19291 1.38692 beta[6] 1.29616 1.48652 1.5834631 1.67931 1.86601 beta[7] 1.66909 1.89193 2.0064159 2.11760 2.34457 beta[8] -0.07222 -0.01275 0.0022081 0.02050 0.11890 beta[9] -0.06681 -0.01646 -0.0007303 0.01404 0.06191 beta[10] -0.06310 -0.01421 0.0007147 0.01645 0.06935 beta0 0.80760 0.89115 0.9327129 0.97590 1.05674
This tutorial has introduced the Bayesian Lasso and Bayesian SSL methods as powerful tools for analyzing regression models with compositional predictors. These Bayesian techniques offer distinct advantages, including the ability to incorporate prior knowledge, manage a large number of covariates, and handle exact collinearity and sparsity in data. We provided a detailed walkthrough of the Bayesian Lasso and SSL methods implemented in JAGS, designed to equip researchers and analysts with the practical skills needed to apply Bayesian techniques to compositional data. While the tutorial has focused on compositional predictors, it is important to note that including continuous predictors alongside compositional ones is a common scenario in practice. For analyses involving continuous predictors alongside compositional ones, readers can easily modify the JAGS code structure presented here and add other predictors. Additionally, while JAGS is our chosen software for demonstration, alternatives like Stan may offer different benefits, and we include a Stan code example in the Appendix for further exploration. In summary, this tutorial offers a practical foundation for applying Bayesian methods to regression with compositional predictors, with guidance for extending the analysis to more complex scenarios.
Aitchison, J. (1986). The statistical analysis of compositional data. Journal of the Royal Statistical Society: Series B (Methodological), 48(3), 139–177. doi: https://doi.org/10.1007/978-94-009-4109-0
Aitchison, J., & Bacon-Shone, J. (1984). The multivariate poisson-log normal distribution. Biometrika, 71(2), 299–307. doi: https://doi.org/10.1093/biomet/76.4.643
Andrews, D. F., & Mallows, C. L. (1974). Scale mixtures of normal distributions. Journal of the Royal Statistical Society: Series B (Methodological), 36(1), 99–102. doi: https://doi.org/10.1111/j.2517-6161.1974.tb00989.x
Belsley, D. A., Kuh, E., & Welsch, R. E. (1980). Regression diagnostics: Identifying influential data and sources of collinearity. John Wiley & Sons. doi: https://doi.org/10.1002/0471725153
Chastin, S., Palarea-Albaladejo, J., Dontje, M., & Skelton, D. (2015). Combined effects of time spent in physical activity, sedentary behaviors and sleep on obesity and cardio-metabolic health markers: A novel compositional data analysis approach. Plos One, 10(10), e0139984. doi: https://doi.org/10.1371/journal.pone.0139984
Deshpande, S., Ročková, V., & George, E. (2019). Simultaneous variable and covariance selection with the multivariate spike-and-slab lasso. Journal of Computational and Graphical Statistics, 28(4), 921–931. doi: https://doi.org/10.1080/10618600.2019.1593179
Egozcue, J. J., Pawlowsky-Glahn, V., Mateu-Figueras, G., & Barceló-Vidal, C. (2003). Isometric logratio transformations for compositional data analysis. Mathematical Geology, 35(3), 279–300. doi: https://doi.org/10.1023/A:1023818214614
Friedman, J., Hastie, T., & Tibshirani, R. (2010). A note on the group lasso and a sparse group lasso. arXiv preprint arXiv:1001.0736.
George, E. I., & McCulloch, R. E. (1993). Variable selection via gibbs sampling. Journal of the American Statistical Association, 88(423), 881–889. doi: https://doi.org/10.1080/01621459.1993.10476353
Ghosh, P., Tang, X., Ghosh, M., & Chakrabarti, A. (2013). Asymptotic properties of bayes risk of a general class of shrinkage priors in multiple hypothesis testing under sparsity. Bayesian Analysis, 11(3). doi: https://doi.org/10.1214/15-ba973
Li, G., Li, Y., & Chen, K. (2023, Jun). It’s all relative: Regression analysis with compositional predictors. Biometrics, 79(2), 1318–1329. doi: https://doi.org/10.1111/biom.13703
Li, Z., McCormick, T., & Clark, S. (2019). Bayesian joint spike-and-slab graphical lasso. In Proceedings of the 36th international conference on machine learning (Vol. 97, pp. 3877–3885). Long Beach, California, USA.
Lin, W., Shi, P., Feng, R., & Li, H. (2014). Variable selection in regression with compositional covariates. Biometrika, 101(4), 785–797. doi: https://doi.org/10.1093/biomet/asu031
Palarea-Albaladejo, J., & Martin-Fernandez, J. A. (2013). zcompositions–r package for multivariate imputation of left-censored data under a compositional approach. Chemometrics and Intelligent Laboratory Systems, 120, 31–38. doi: https://doi.org/10.1016/j.chemolab.2015.02.019
Park, T., & Casella, G. (2008). The Bayesian lasso. Journal of the American Statistical Association, 103(482), 681–686. doi: https://doi.org/10.1198/016214508000000337
Plummer, M. (2003). Jags: A program for analysis of bayesian graphical models using gibbs sampling [Computer software manual]. Retrieved from https://mcmc-jags.sourceforge.io/
R Core Team. (2023). R: A language and environment for statistical computing [Computer software manual]. Vienna, Austria. Retrieved from https://www.R-project.org/
Ročková, V., & George, E. I. (2016). Fast bayesian factor analysis via automatic rotations to sparsity. Journal of the American Statistical Association, 111(516), 1608–1622. doi: https://doi.org/10.1080/01621459.2016.1192541
Ročkov’a, V., & George, E. I. (2018). Spike-and-slab lasso. Journal of the American Statistical Association, 113(521), 431–444. doi: https://doi.org/10.1080/01621459.2016.1260469
Tang, Z., Shen, Y., Li, Y., Zhang, X., Wen, J., Qian, C., … Yi, N. (2018). Group spike-and-slab lasso generalized linear models for disease prediction and associated genes detection by incorporating pathway information. Bioinformatics, 34(6), 901–910. doi: https://doi.org/10.1093/bioinformatics/btx714
Tang, Z., Shen, Y., Zhang, X., & Yi, N. (2017a). The spike-and-slab lasso cox model for survival prediction and associated genes detection. Bioinformatics, 33(18), 2799–2807. doi: https://doi.org/10.1093/bioinformatics/btx300
Tang, Z., Shen, Y., Zhang, X., & Yi, N. (2017b). The spike-and-slab lasso generalized linear models for prediction and associated genes detection. Genetics, 205(1), 77–88. doi: https://doi.org/10.1534/genetics.116.192203
Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58(1), 267–288. doi: https://doi.org/10.1111/j.2517-6161.1996.tb02080.x
Zou, H., & Hastie, T. (2005). Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 67(2), 301–320. doi: https://doi.org/10.1111/j.1467-9868.2005.00503.x
In the appendix of this tutorial, we present an implementation of the Bayesian Lasso using the Stan programming language. Note that Stan does not support discrete parameters, which is a prerequisite for implementing the Bayesian SSL model. As such, we currently are only able to provide the Bayesian Lasso implementation within the Stan framework.
stan_model_code<- " data { int<lower=0> N; // Number of observations int<lower=0> p; // Number of predictors matrix[N, p] X; // Predictor matrix vector[N] y; // Response variable real<lower=0> lambda; // Lasso penalty parameter } parameters { real beta0; // Intercept vector[p] beta; // Coefficients for predictors real<lower=0> sigma; // Standard deviation of errors vector<lower=0>[p] tau_sq; // Scale parameter for Laplace prior } model { // Likelihood for (i in 1:N) { y[i] ~ normal(beta0 + dot_product(beta, X[i]), sigma); } // Priors beta0 ~ normal(0, 100); // Weakly informative prior for the intercept sigma ~ cauchy(0, 2.5); // Cauchy prior for sigma for (j in 1:p) { tau_sq[j] ~ exponential(lambda^2 / 2); // Exponential prior for tau_sq } // Conditional prior for beta using scale mixture representation for (j in 1:p) { beta[j] ~ normal(0, sqrt(tau_sq[j] * sigma^2)); // Laplace prior represented as scale mixture } } " y<-as.vector(y) # Initial values for the parameters lambda <- p * sqrt(var(lm(y ~ X - 1)$residuals)) / sum(abs(lm(y ~ X - 1)$coefficients)) # Compile the Stan model sm <- stan_model(model_code = stan_model_code) # Run the initial model fit <- sampling(sm, data = list(N = N, p = p, X = X, y = y, lambda = lambda),iter = 2000, chains = 1, warmup = 500, thin = 1)