Semiparametric Bayesian Methods in Growth Curve Modeling for Nonnormal Data Analysis
DOI:
https://doi.org/10.35566/jbds/v1n1/p4Keywords:
Semiparametric Bayesian methods, Growth curve modeling, Robust analysis, Dirichlet process mixtureAbstract
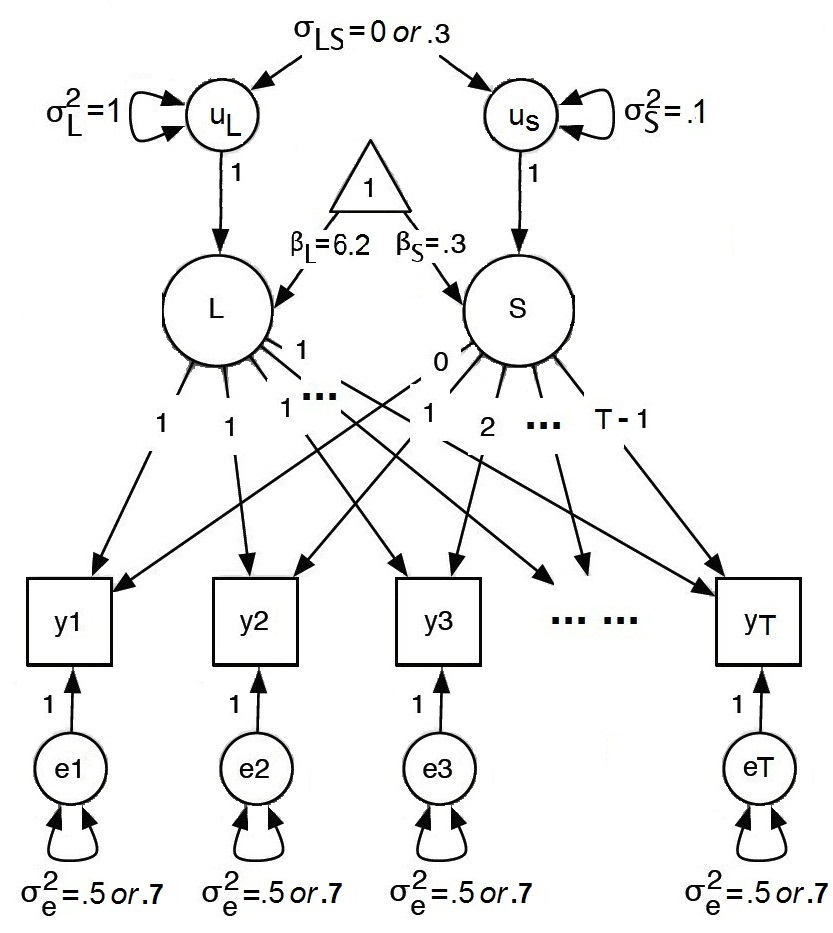
Semiparametric Bayesian methods have been proposed in the literature for growth curve modeling to reduce the adverse effect of having nonnormal data. The normality assumption of measurement errors in traditional growth curve models was replaced by a random distribution with Dirichlet process mixture priors. However, both the random effects and measurement errors are equally likely to be nonnormal. Therefore, in this study, three types of robust distributional growth curve models are proposed from a semiparametric Bayesian perspective, in which random coefficients or measurement errors follow either normal distributions or unknown random distributions with Dirichlet process mixture priors. Based on a Monte Carlo simulation study, we evaluate the performance of the robust models and demonstrate that selecting an appropriate model for practical data analyses is very important, by comparing the three types of robust distributional models as well as the traditional growth curve models with the normality assumption. We also provide a straightforward strategy to select the appropriate model.