Moments Calculation for the Doubly Truncated Multivariate Normal Density
DOI:
https://doi.org/10.35566/jbds/v1n1/p2Keywords:
Multivariate normal, Double truncation, Moment generating function, Bivariate marginal density function, Graphical models, Conditional independenceAbstract
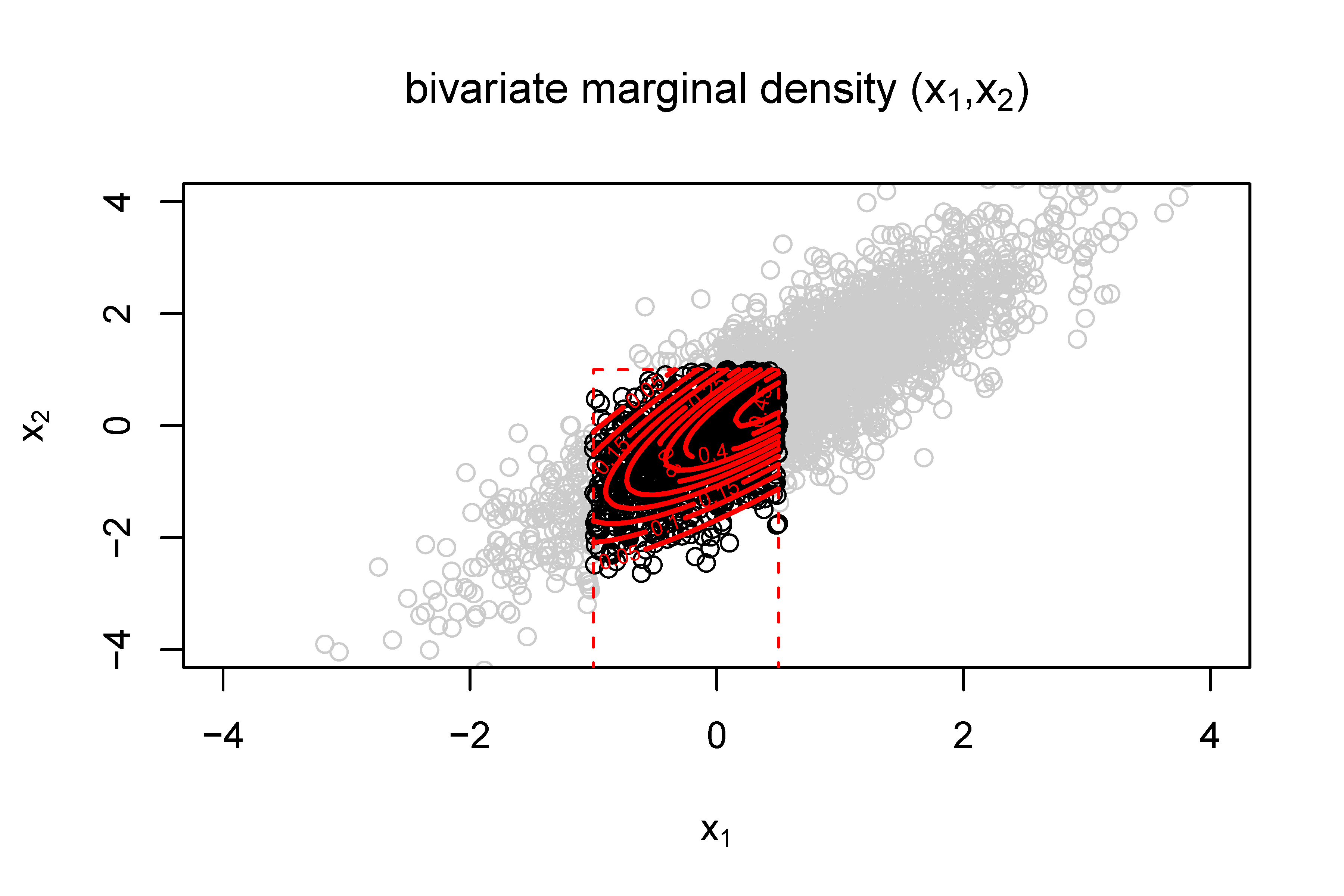
In the present article, we derive an explicit expression for the truncated mean and variance for the multivariate normal distribution with arbitrary rectangular double truncation. We use the moment generating approach of Tallis (1961) and extend it to general μ, Σ and all combinations of truncation. As part of the solution, we also give a formula for the bivariate marginal density of truncated multinormal variates. We also prove an invariance property of some elements of the inverse covariance after truncation. Computer algorithms for computing the truncated mean, variance and the bivariate marginal probabilities for doubly truncated multivariate normal variates have been written in R and are presented along with three examples.