Two-step growth mixture model to examine heterogeneity in nonlinear trajectories
DOI:
https://doi.org/10.35566/jbds/v1n2/p4Keywords:
Growth Mixture Models, Nonlinear Trajectories, Individual Measurement Occasions, Covariates, Simulation Studies, Exploratory Factor AnalysisAbstract
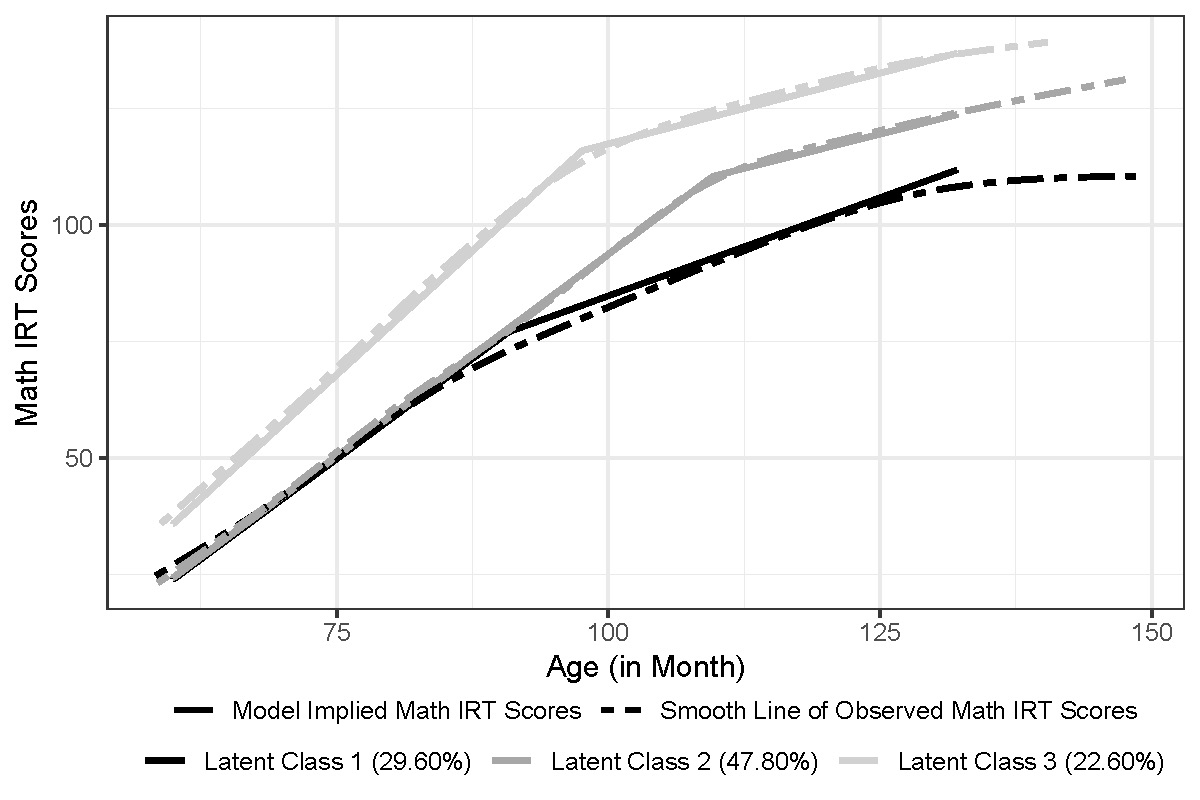
Empirical researchers are usually interested in investigating the impacts that baseline covariates have when uncovering sample heterogeneity and separating samples into more homogeneous groups. However, a considerable number of studies in the structural equation modeling (SEM) framework usually start with vague hypotheses in terms of heterogeneity and possible causes. It suggests that (1) the determination and specification of a proper model with covariates is not straightforward, and (2) the exploration process may be computationally intensive given that a model in the SEM framework is usually complicated and the pool of candidate covariates is usually huge in the psychological and educational domain where the SEM framework is widely employed. Following Bakk and Kuha (2017), this article presents a two-step growth mixture model (GMM) that examines the relationship between latent classes of nonlinear trajectories and baseline characteristics. Our simulation studies demonstrate that the proposed model is capable of clustering the nonlinear change patterns, and estimating the parameters of interest unbiasedly, precisely, as well as exhibiting appropriate confidence interval coverage. Considering the pool of candidate covariates is usually huge and highly correlated, this study also proposes implementing exploratory factor analysis (EFA) to reduce the dimension of covariate space. We illustrate how to use the hybrid method, the two-step GMM and EFA, to efficiently explore the heterogeneity of nonlinear trajectories of longitudinal mathematics achievement data.