A Weighted Residual Bootstrap Method for Multilevel Modeling with Sampling Weights
DOI:
https://doi.org/10.35566/jbds/v1n2/p6Keywords:
Bootstrap, Informative selection, Multilevel modeling, Sampling weights, Pseudo-maximum likelihoodAbstract
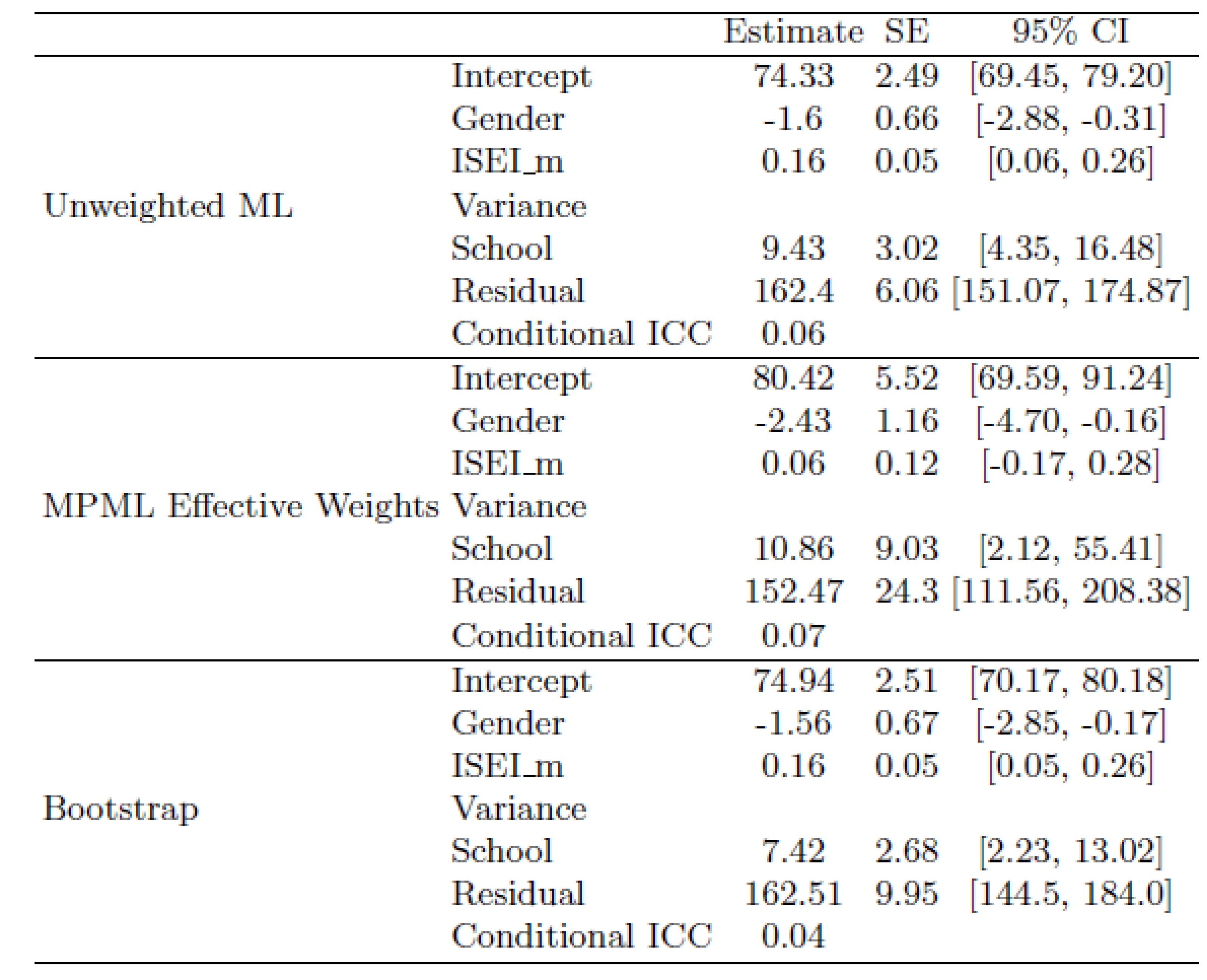
Multilevel modeling is often used to analyze survey data collected with a multistage sampling design. When the selection is informative, sampling weights need to be incorporated in the estimation. We propose a weighted residual bootstrap method as an alternative to the multilevel pseudo-maximum likelihood (MPML) estimators. In a Monte Carlo simulation using two-level linear mixed effects models, the bootstrap method showed advantages over MPML for the estimates and the statistical inferences of the intercept, the slope of the level-2 predictor, and the variance components at level-2. The impact of sample size, selection mechanism, intraclass correlation (ICC), and distributional assumptions on the performance of the methods were examined. The performance of MPML was suboptimal when sample size and ICC were small and when the normality assumption was violated. The bootstrap estimates performed generally well across all the simulation conditions, but had notably suboptimal performance in estimating the covariance component in a random slopes model when sample size and ICCs were large. As an illustration, the bootstrap method is applied to the American data of the OECD’s Program for International Students Assessment (PISA) survey on math achievement using the R package bootmlm.