A Multiple Imputation Approach for Handling Missing Data in Classification and Regression Trees
DOI:
https://doi.org/10.35566/jbds/v1n1/p6Keywords:
Multiple Imputation, Classification and Regression Tree (CART), Missing DataAbstract
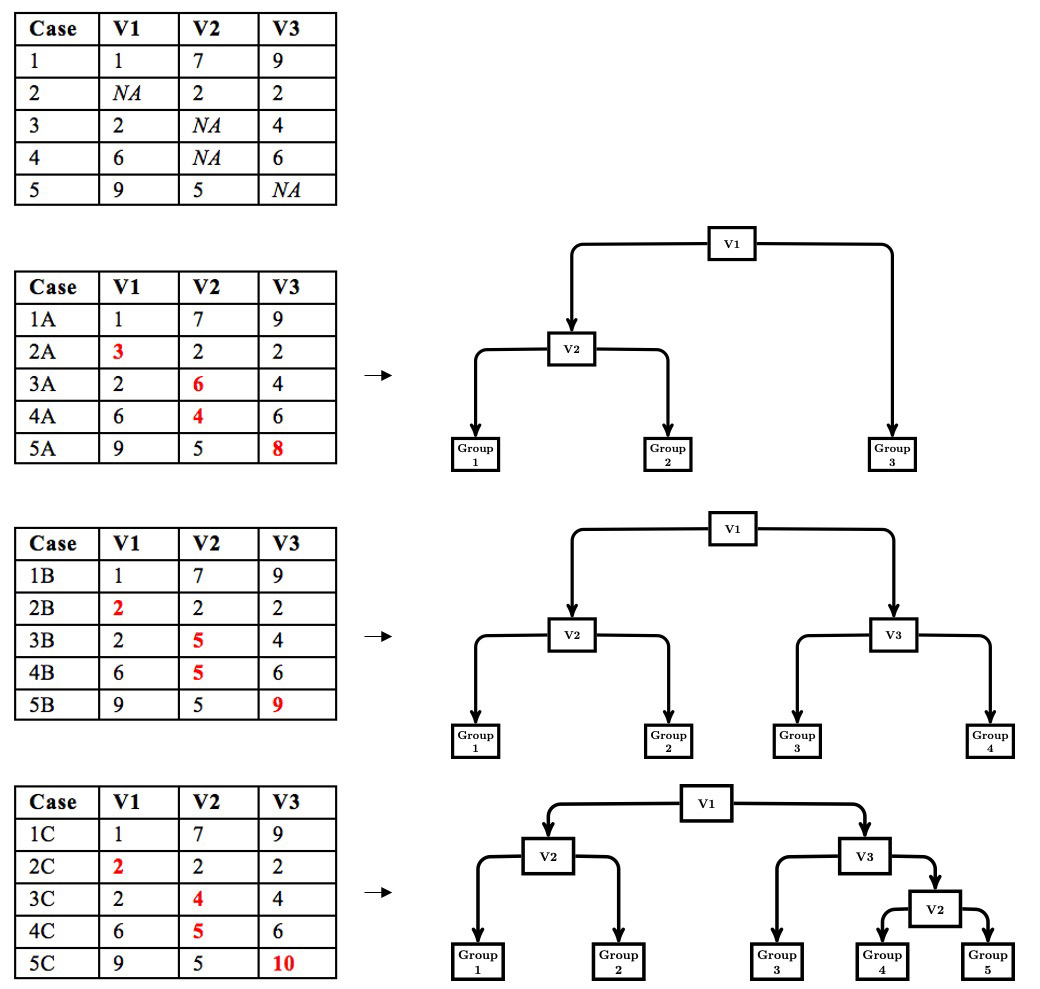
Decision trees (DTs) is a machine learning technique that searches the predictor space for the variable and observed value that leads to the best prediction when the data are split into two nodes based on the variable and splitting value. The algorithm repeats its search within each partition of the data until a stopping rule ends the search. Missing data can be problematic in DTs because of an inability to place an observation with a missing value into a node based on the chosen splitting variable. Moreover, missing data can alter the selection process because of its inability to place observations with missing values. Simple missing data approaches (e.g., listwise deletion, majority rule, and surrogate split) have been implemented in DT algorithms; however, more sophisticated missing data techniques have not been thoroughly examined. We propose a modified multiple imputation approach to handling missing data in DTs, and compare this approach with simple missing data approaches as well as single imputation and a multiple imputation with prediction averaging via Monte Carlo Simulation. This study evaluated the performance of each missing data approach when data were MAR or MCAR. The proposed multiple imputation approach and surrogate splits had superior performance with the proposed multiple imputation approach performing best in the more severe missing data conditions. We conclude with recommendations for handling missing data in DTs.