A New Bayesian Structural Equation Modeling Approach with Priors on the Covariance Matrix Parameter
DOI:
https://doi.org/10.35566/jbds/v2n2/p2Keywords:
Structural equation modeling, Bayesian analysis, Inverse Wishart prior, Informative prior, Convergence diagnosticsAbstract
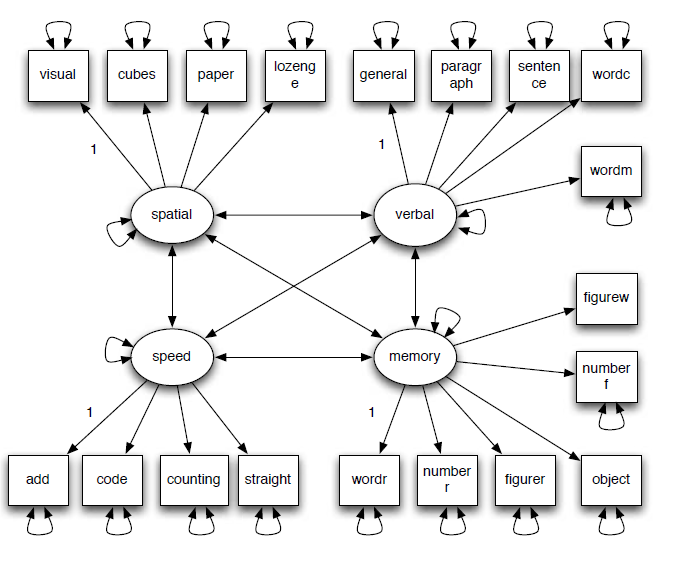
Bayesian inference for structural equation models (SEMs) is increasingly popular in social and psychological sciences owing to its flexibility to adapt to more complex models and the ability to include prior information if available. However, there are two major hurdles in using the traditional Bayesian SEM in practice: (1) the information nested in the prior distributions is hard to control, and (2) the MCMC iterative procedures naturally lead to Markov chains with serial dependence and the diagnostics of their convergence are often difficult. In this study, we present an alternative procedure for Bayesian SEM aiming to address the two challenges. In the new Bayesian SEM procedure, we specify a prior distribution on the population covariance matrix parameter Σ and obtain its posterior distribution p(Σ|data). We then construct a posterior distribution of model parameters θ in the hypothetical SEM model by transforming the posterior distribution of Σ to a distribution of model parameter θ. The new procedure eases the practice of Bayesian SEM significantly and has a better control over the information nested in the prior distribution. We evaluated its performance through a simulation study and demonstrate its application through an empirical example.